Three cars of mass m each are held at rest on an inclined smooth railway track of inclination θ using an elastic cable (Assume that the cable behaves like a spring even during compression) that is parallel to the incline. The cable is observed to stretch by a length x just before a coupling breaks, detaching one of the cars.

the frequency of the resulting oscillations of the remaining two cars is 12π√3gsinθx
the frequency of the reulting oscillations of the remaining two cars is 12π√3gsinθx
the amplitude of the oscillations mentioned in above options is 2x3
the amplitude of the oscillations mentioned in above options is x3
The correct Answer is:A, D
(A) The net force on the three cars is zero before the cable breaks. There are three forces on the cars: the weight, W, a normal force, N, and the upward force from the cable, f. Then
F=Wsinθ=3mgsinθ
This force is from the elastic properties of the cable,
so k=Fx=3mgsinθx
The frequency of oscillation of the remaining two can after the bottom car is released is
f=22π√k2m=12π√3mgsinθ2mx=12x√3gsinθ2x
(B) Each car contributes equally to the stretching of the cable, so one car causes the cable to stretch x3
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:ASSERTION & REASON QUESTIONS
Explore 13 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL-V
Explore 1 Video
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:NCERT BASED QUESTIONS
Explore 1 Video
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
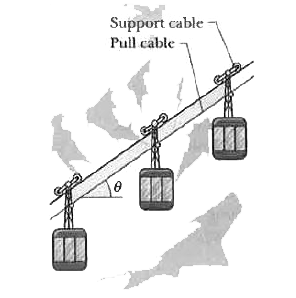
Figure 5-60 shows a section of a cable-car system. The maximum permissible mass of each car with occupants is 2750 kg. The cars, riding on a support cable, are pulled by a second cable attached to the support tower on each car. Assume that the cables are taut and inclined at angle θ=35∘. What is the difference in tension between adjacent sections of pull cable if the cars are at the maximum permissible mass and are being accelerated up the incline at 0.81 m/s2 ?
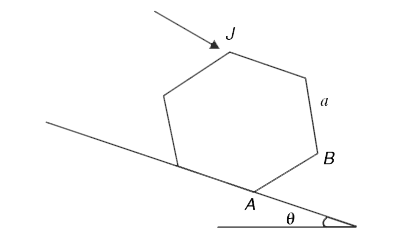
View SolutionA hexagonal pencil of mass M and sides length a has been placed on a rough incline having inclination θ Friction is large enough to prevent sliding. If at all the pencil moves, during one full rotation each of its 6 edges, in turn, serve as instantaneous axis of rotation.
(a) Show that for θ>30∘ the pencil cannot remain at rest.
(b) For inclination of incline θ<30∘ the pencil will not roll on its own. A sharp impulse J is given to the pencil parallel to the incline at its upper edge (see figure). Friction does not allow the pencil to slide but it begins to rotate about the edge through A with initial angular speed ω0. Find ω0. Moment of inertia of the pencil about its edge is I.
(c) Find minimum value of J so that the pencil will turn about A, and B will land on the incline.
(d) If kinetic energy acquired by the pencil just after the impulse is K0, find its kinetic energy just before edge B lands on the incline
View Solution
Knowledge Check
A cart of mass 3m is on a smooth horizontal ground. The cart surface consists of an incline plane AB and horizontal surface BD both of which are frictionless. The cart is initially at rest and a small block of mass m is released from point A. Assume that the corner B is rounded so that mass in passes it smoothly. The length of part BD of car be L and the vartical height of incline plane AB be h as shown in digram

Select correct option(s)ATime taken by the block to slide from B to D on the cart is √3L28ghBTime taken by the block to slide from B to D on the cart is √L28ghCcomponent of momentum (in horizontal direction) of system is conserved from A to BDcomponent of momentum (in vertical direction) of system is conserved from A to BA cart of mass 3m is on a smooth horizontal ground. The cart surface consists of an incline plane AB and horizontal surface BD both of which are frictionless. The cart is initially at rest and a small block of mass m is released from point A. Assume that the corner B is rounded so that mass in passes it smoothly. The length of part BD of car be L and the vartical height of incline plane AB be h as shown in digram

Select correct option(s)AThe distance moved by the cart during the time interval in which block slides from B to D is L4.BThe distance moved by the cart during the time interval in which block slides from B to D is L3.CFrom B to C acceleration of block is constantDFrom B to C acceleration of block is zeroA smooth wedge of mass m and angle of inclination 60∘ rests unattached between two springs of spring constant K and 4k on a smooth horizontal plane both springs in the unextended position the time period of small oscillation of the wedge (assuming that the springs are constrained to get compressed along their length) equals
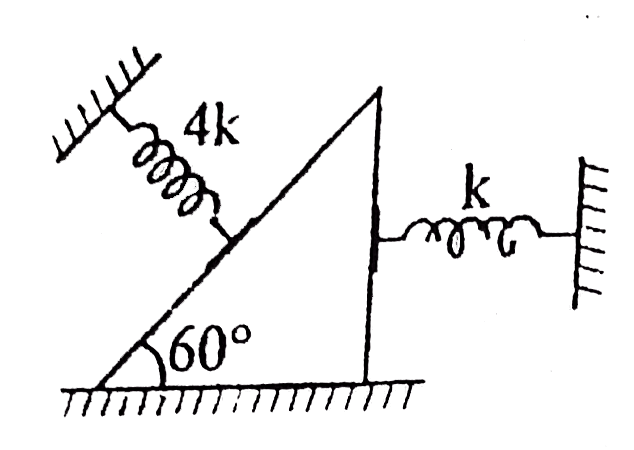 Aπ(1+12)√mkBπ(1+1√3)√mkCπ(1+2√3)√mkDnone of the above
Aπ(1+12)√mkBπ(1+1√3)√mkCπ(1+2√3)√mkDnone of the above
An ideal massles spring S can be compressed 1 m by a force of 100 N in equilibrium. The same spring is placed at the bottom of a frictionless plane inclined at 30∘ to the horizontal. A 10 kg block M is released from rest at the top of the incline and is brought to rest momentarily after compressing the spring by 2 m. If g=10m/s2, the speed of mass just before it touches the spring is √10xm/s. Find value of x?

View Solution(i) O is a fixed peg at a height H above a perfectly inelastic smooth horizontal plane. A light inextensible string of length L(>H) has one end attached to O and the other end is attached to a heavy particle. The particle is held at the level of O with string horizontal and just taut and released from rest. Find the height of the particle above the plane when it comes to rest for the first time after the release.
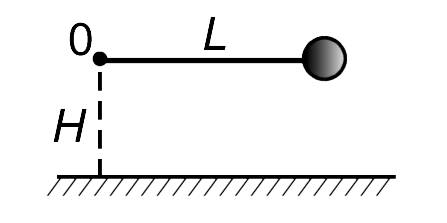
(ii) The bob of a pendulum has mass m and the length of pendulum is l. It is initially at rest with the string vertical and the point of suspension at a height 2l above the floor. A particle P of mass m2 moving horizontally along –ve x-direction with velocity √2gl collides with the bob and comes to rest. The bob swings and when it comes to rest for the first time, another particle Q of mass m moving horizontally along y direction collides with the bob and sticks to it. It is observed that the bob now moves in a horizontal circle.
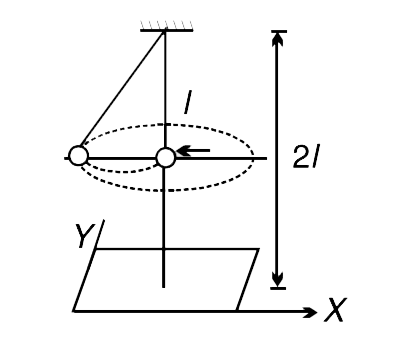
(a) Find tension in string just before the second collision.
(b) Find the height of the circular path above the floor.
(c) Find the time period of the circular motion.
(d) The string breaks during the circular motion at time t=0. At what time the bob will hit the floor ?
View SolutionA particle of mass m comes down on a smooth inclined plane from point B at a height of h from rest. The magni-tude of change in momentum of the particle between position A (just before arriving on horizontal surface) and C (assuming the angle of inclination of the plane as θ with respect to the horizontal) is

View SolutionAn ideal massless spring S can compressed 1.0 m in equilibrium by a force of 1000N. This same spring is placed at the bottom of a friction less inclined plane which makes an angle θ=30∘ with the horizontal. A (10 kg) mass (m) is released from rest at the top of the incline and and is brought to rest momentarily after compressing the spring by 2m. If g=10ms−1, what is the speed of just before it touches the spring?
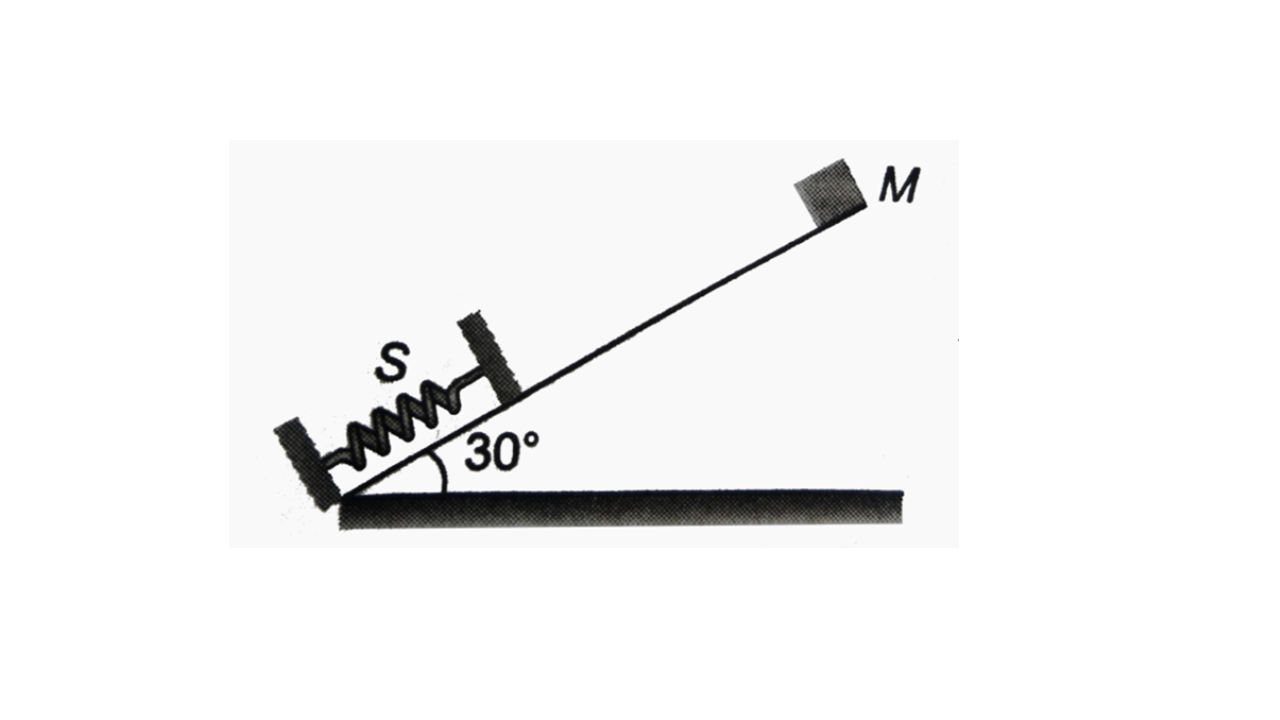 .
.
View SolutionWhen a tensile or compressive load 'P' is applied to rod or cable, its length changes. The change length x which, for an elastic material is proportional to the force Hook' law).
Pαx or P=kx
The above equation is similar to the equation of spring. For a rod of length L, area A and young modulue Y. the extension xcan be expressed as.
x=PLAY or P=AYx, hence K=AYL
Thus rod or cables attached to lift can be treated as springs. The energy stored in rod is called stra energy & equal to 12Px. The loads placed or dropped on the floor of lift cause stresses in the cable and can be evaluted by spring analogy. If the cable of lift cause stresses and load is placed dropped, then maximum extension in cable can be calculated by enerfy conservation.
Four identical rods of geometry as described in problem (2) are attached with lift. If weight of the lift cage is 1000N, and elastic limit of each rod is taken as 9×104N/m2 then the number of persons it can carry safety is equal to. (g=10m/sec2), assume average mass of a person as 50kg and lift moves with constant speed)
View Solution

