A block A of mass m is attached at one end of a light spring and the other end of the spring is connected to another block B of mass 2m through a light string as shown in the figure. A is held and B is in static equilibrium. Now A is released. The acceleration of A just after that instant is a . In the next case, B is held and A is in static equilibrium. Now when B is released, its acceleration immediately after the release is b . The value of a/b is (pulley, string and the spring are massless).

0
undefined
2
12
The correct Answer is:C
For first case tension in spring will be
Ts=2mg just after 'A' is released.
2mg−mg=ma implies a=g
In second case Ts=mg
2mg−mg=2mb
b=g/2
a/b=2 . 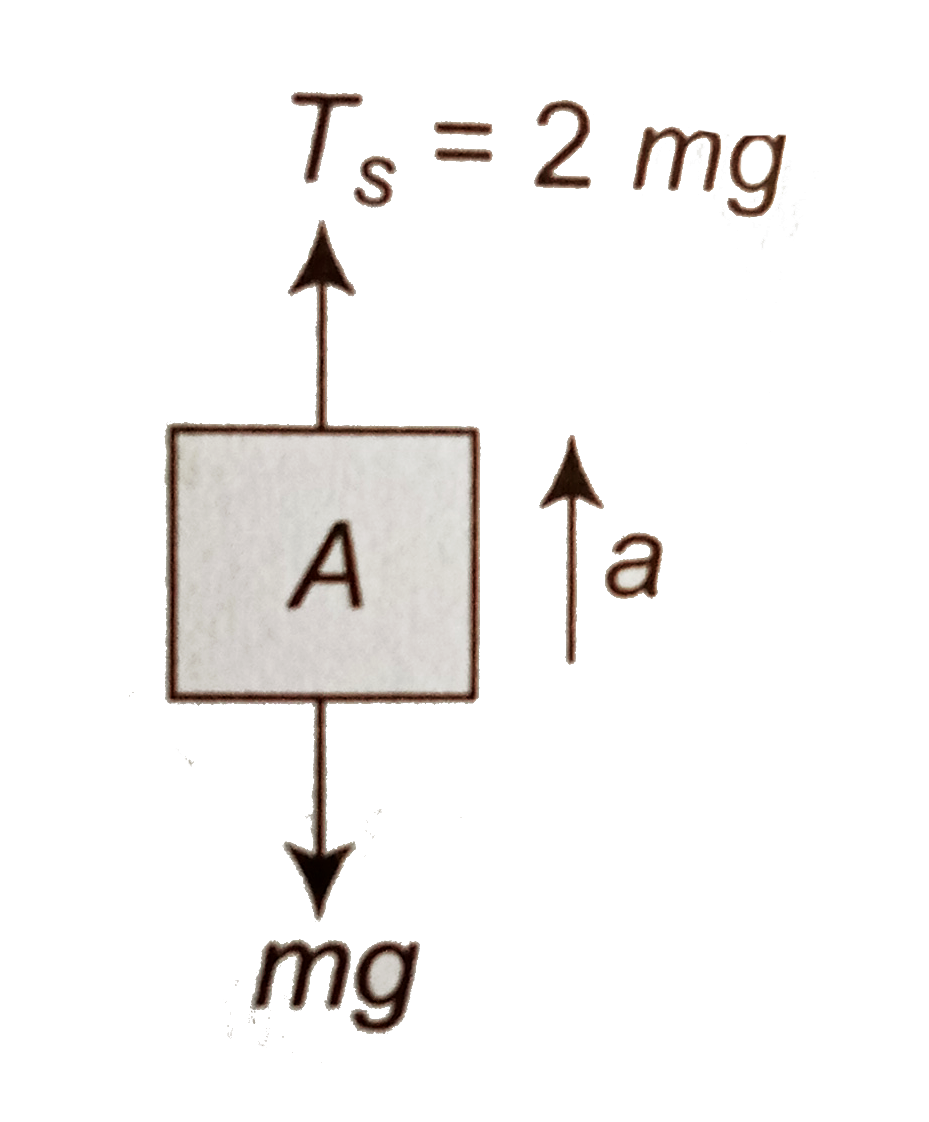
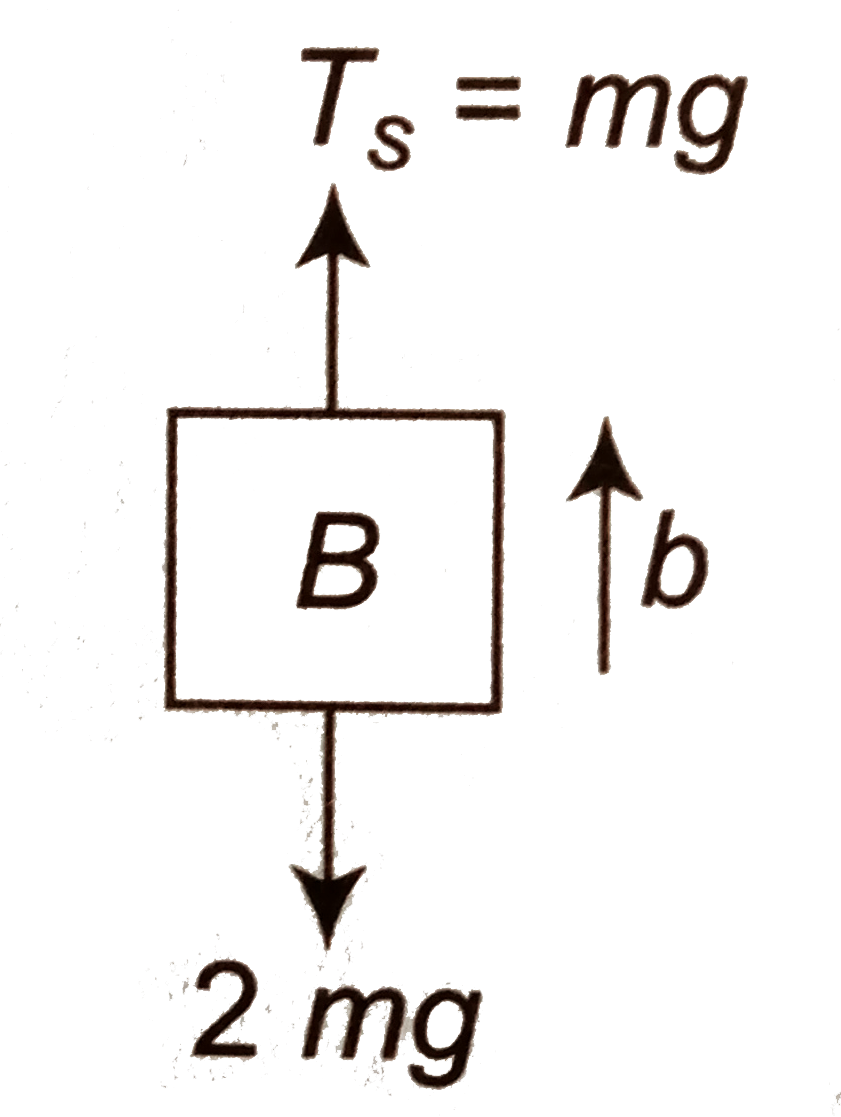
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Assertion Reasoning
14 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - NEET Questions
38 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Dynamics Of Circular Motion
31 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test
29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
Similar Questions
Two block A and B of mass M & 3M are connected through a light string. One end of the string is connected to the blcok B and its other end is connected to a fixed point S as shown in fig. Now a force F is applied to block B. find the acceleration of block A & B.

View SolutionTwo blocks of masses M and 2M are connected to each other through a light spring as shown in figure . If we push the mass M with a force F which cause acceleration a in mass M. what will the acceleration in 2M?
View Solution
Knowledge Check
A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2kA Bead of mass m is attached to one end of a spring of natural length 'R' and spring cosntant 'k=(√3+1)mgR'. The other end of the spring is fixed at point 'A' on a smooth vertical ring of radius 'R' as shown
 Amg/2B√3mgC3√3mgD3√3mg2
Amg/2B√3mgC3√3mgD3√3mg2Two blocks of masses 2m and m are in equilibrium a shown in the figure. Now the string between the blocks is suddenly broken. The accelarations of the blocks A and B respectively, at that instant are
 Ag and gBg and g2Cg2 and gDg2and g2
Ag and gBg and g2Cg2 and gDg2and g2
Two blocks A and B of same mass m attached with a light string are suspended by a spring as shown in fig. Find the acceleration of block A and B just after the string is cut.

View SolutionTwo blocks A and B of same mass m attached with a light spring are suspended by a string as shown in fig. Find the acceleration of block A and B just after the string is cut.
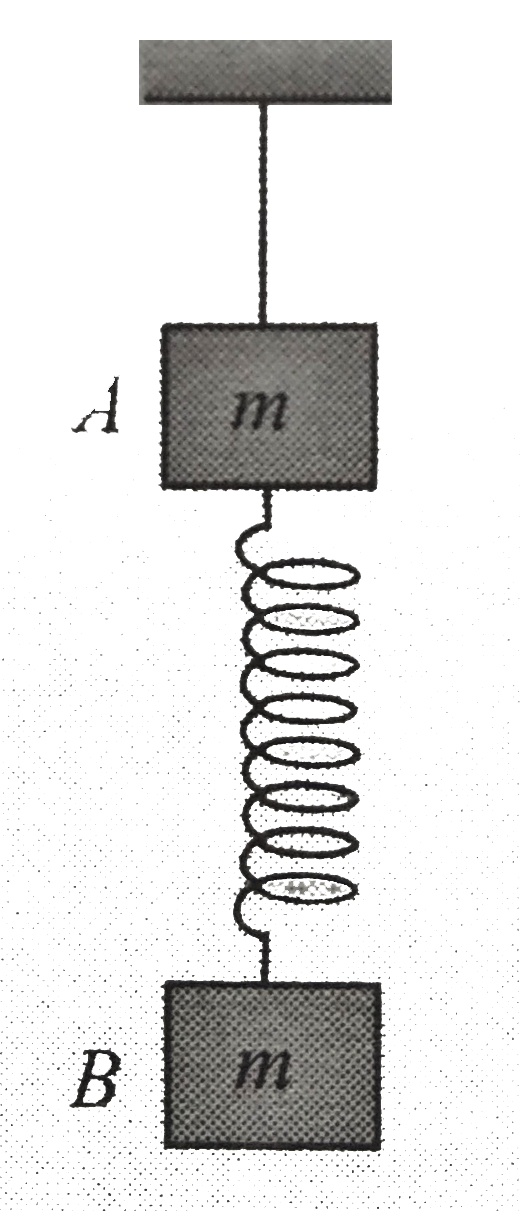
View SolutionUniform rod AB is hinged at end A in horizontal position as shown in the figure the other end is connected to a block through a massless string m as shown the pulley is smooth and massless masses of block and rod is same and is equal to m then acceleration of block just after release from this position is

View Solution
Uniform rod AB is hinged at end A in horizontal position as shown in the figure. The other end is connected to a block through a massless string as shown. The pulley is smooth and massless. Mass of block and rod is same and is equal to m Then acceleration of block just after release from this position is
View SolutionA bead of mass 'm' is attached to one end of a spring of natural length R & spring constant k=(√3+1)R. The other end of the spring is fixed at point A on a smooth vertical ring of radius R as shown. The normal reaction at B just after it is released to move is

View Solution