The charge on a capacitor decrease η time in time t, when it discharging through a circuit with a time constantτ
t=ητ
t=τ1nη
t=τ(1nη−1)
t=τ1n(1−1η)
The correct Answer is:B
q=q0e−t/τ
q0η=q0e−t/τ
et/τ=η⇒t=τlnη
Topper's Solved these Questions
- THERMAL AND ELECTRIC EFFECT oF CURRENTBook:CP SINGHChapter:THERMAL AND ELECTRIC EFFECT oF CURRENTExercise:Exercises
Explore 101 Videos
- SEMICONDUCTORSBook:CP SINGHChapter:SEMICONDUCTORSExercise:Exercises
Explore 140 Videos
- WAVE NATURE OF LIGHTBook:CP SINGHChapter:WAVE NATURE OF LIGHTExercise:EXERCISES
Explore 140 Videos
Similar Questions
Knowledge Check
A capacitor C is connected to two equal resistances as shown in the figure. Consider the following statemets
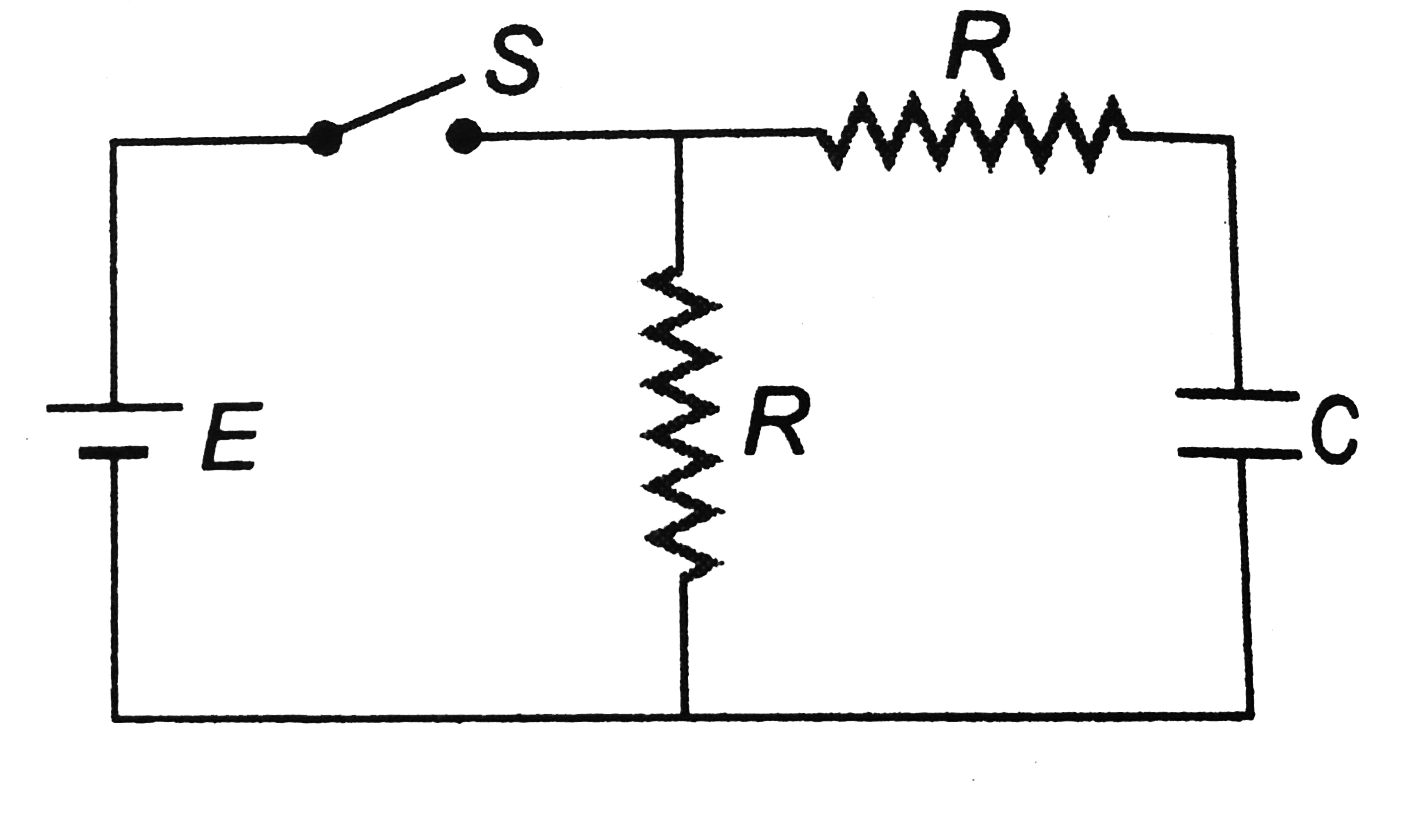
i. At the time of charging of capacitor time constant of the circuit is 2CR
ii. At the time of discharging of the capacitor the time constant of the circuit is CR
iii. At the time of discharging of the capacitor the time constant of the circuit is 2CR
iv At the time of charging of the capacitor the time constant of the circuit is 2CRAstatements i and ii only are correctBstatements ii and iii only are correctCstatements iii and iv only are correctDstatements i and iii only are correctA charged capacitor of capacitance C is discharging through a resistor of resistance R. At what time the charge on the capacitor is equal to one half of its initial value?
ARC2BRCloge2CRC loge2D1RCloge2The time constant of charging of the circuit shown in figure is
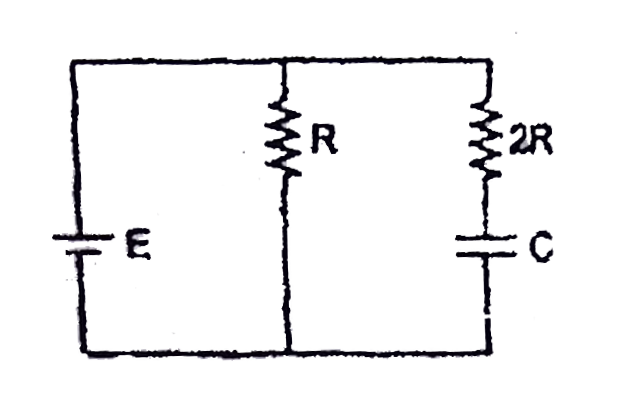 A23RCB2RCC3RCD32RC
A23RCB2RCC3RCD32RC
A capacitor of capacity 1μF is connected in a closed series circuit with a resistance or 107 ohms, an open key and a cell of 2 V with negligible internal resistance :
(i) When the key is switched on at time t=0, find,
(a) The time constant for the circuit.
(b) The charge on the capacitor at steady state.
(c) Time taken to deposit charge equal to half of charge that will deposit at steady state.
(ii) If after completely charging the capacitor, the cell is shorted by zero resistance at time t=0, find the charge on the capacitor at t=50 s. (Given : e−5=6.73×10−3,ln2=0.693)
View SolutionA charged capacitor of capacitance 40μF is discharged through a 50Ω resistance. Determine the time constant of the circuit.
View SolutionA circuit consists of a source of a constant emfξ and a resistance R amd a capacitor with capacitance C connected in series. The internal resistance of the source is negligible. At a moment t=0 the capacitance of the capacitor is abruply decreased η-fold. FInd the current flowing through the circuit as a function of time t.
View SolutionThe charge on a capacitor plate in a circuit, as a function of time, is shown in the figure. What is the value of current at t=4s?
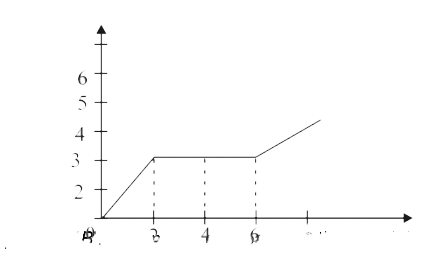
View SolutionA parallel-plate capacitor is filled with a delectric meterial having resistivity(ρ)and dielectric constant K.The capcitor is charged and disconnected from the charging source. The capacitor is slowly discharged through the dielectric.Show that the time constant of the discharge is independent of all gepmetrical parameters like the plate area or separation between the plates. Find this time constant.
View Solution

