Question

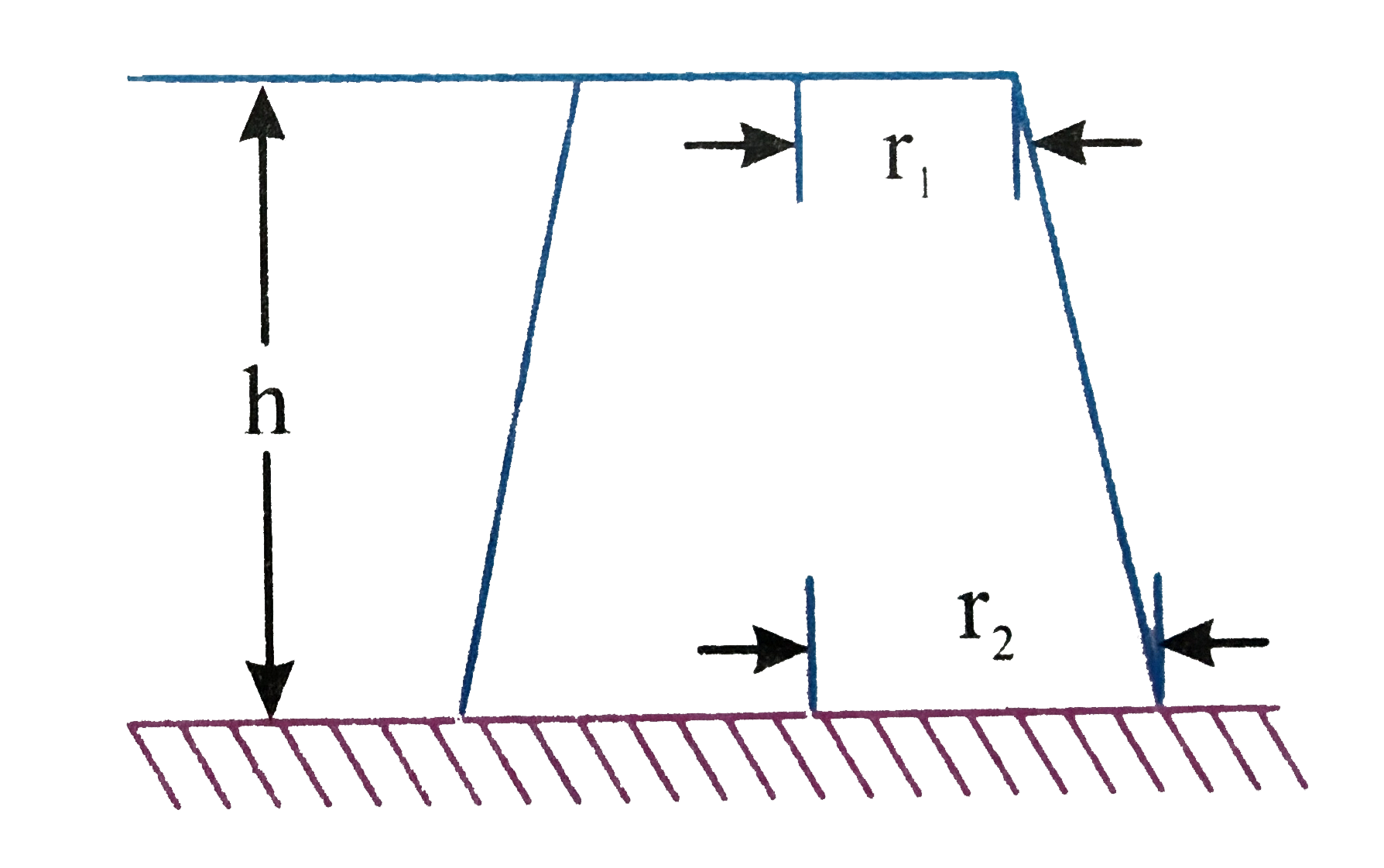
A truncated cone of solid rubber of a mass $M$ is placed verticle. If its linear dimensions are given and $Y$ = Young's modulus of the cone, find the deformation of the cone.

Options

A. `Delta l = (FH)/(2pi r_(1) r_(2) Y)`
B. `Delta l = (FH)/(6pi r_(1) r_(2) Y)`
C. `Delta l = (FH)/(3pi r_(1) r_(2) Y)`
D. `Delta l = (FH)/(pi r_(1) r_(2) Y)`

Answer

D

Explanation

Consider a small elememt at a distance `x` form the top.
let by the elongation of this elemement
`dy = (F dx)/(YA), A = pi r^(2)`

`dx` = length of that element
`F = mg` which is constatn
`r = a + x tan theta`
`dy = (F)/(Y pi) xx int_(0)^(H) (dx)/((a + x tan theta)^(2)), tan theta = (b-a)/(H)`
where `a = r_(1), b = r`
`:. Dl = (FH)/(pi r_(1)(r_(1) + H tan theta)Y), :. Delta l = (FH)/(pi r_(1) r_(2) Y)`