A sphere of mass m attached with the free end of a steel wire of length l swings in the veritical plane form the horizontal positon.
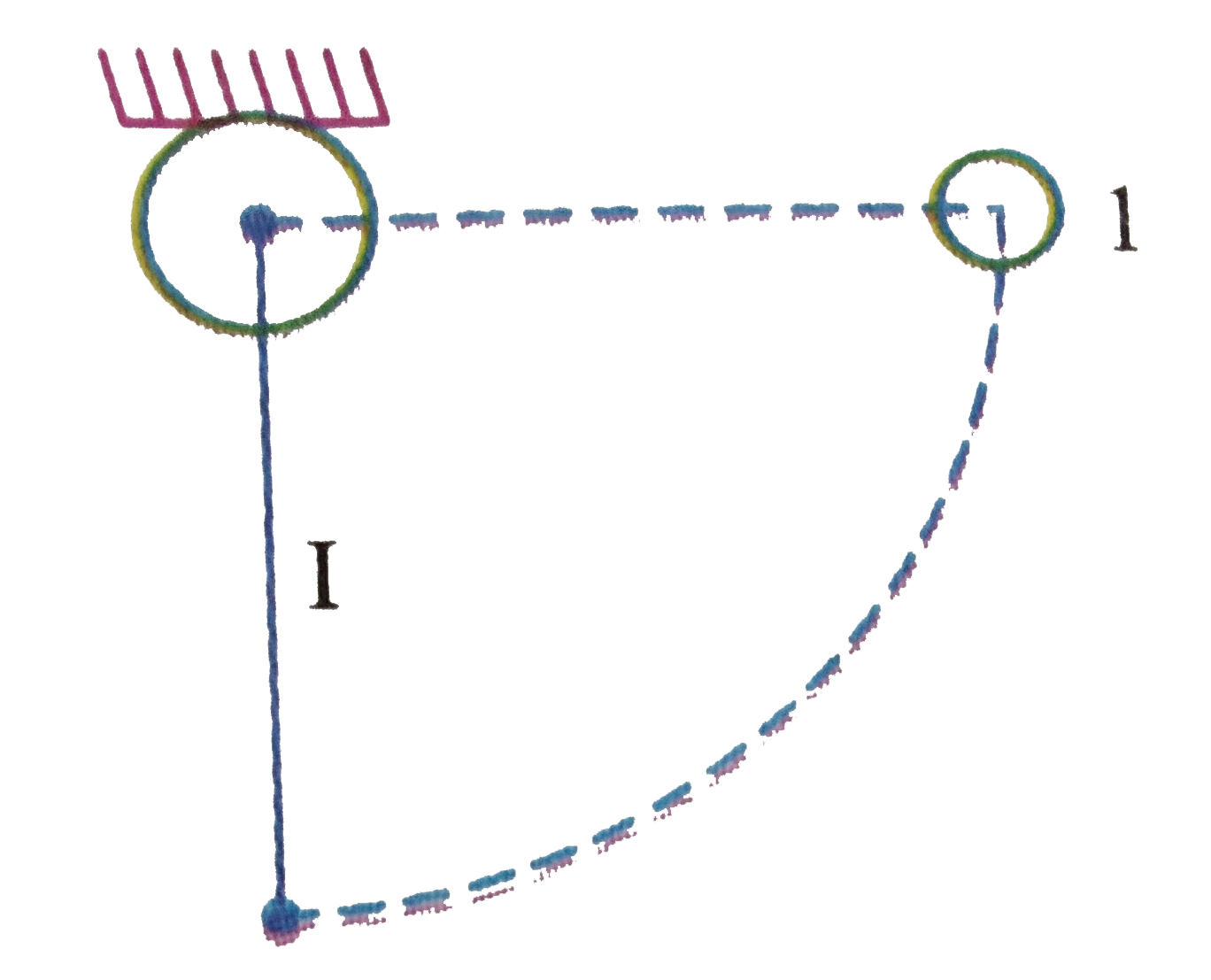
Elongation of the wire in the vericle positon is
mglY(πr2)
2mglY(πr2)
mgl3Y(πr2)
3mglY(πr2)
The correct Answer is:D
Δl=(Fnetl)YA,V=√2gl
=(mg+mv2l)lYA=(mg+2mg)lYA
ΔsL=3mglY(πr2),v=12Fe,U=YA2l×(Δl)2=9m2g2l2Yπr2
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Comprehension-2:
Explore 2 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Comprehension-3:
Explore 2 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:SINGLE ANSWER TYPE QUESTIONS
Explore 13 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:EXERCISE - III
Explore 30 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-II(H.W)
Explore 31 Videos
Similar Questions
A sphere of radius 10cm and mass 25 kg is attached to the lower end of a steel wire of length 5m and diameter 4mm which is suspended from the ceiling of a room . The point of support is 521cm above the floor. When the sphere is set swinging as a simple pendulum, its lowest point just grazes the floor. Calculate the velocity of the ball at its lowest position (Ysteel=2×1011N/m2).
View SolutionA sphere of radius 0.1m and mass 8πkg is attached to the lower end of a steel wire of length 5.0m and diameter 10−3. The wire is suspended from 5.22m high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is (1.994×1011N/m2).
View Solution
Knowledge Check
A sphere of mass m attached with the free end of a steel wire of length l swings in the veritcle plane form the horizontal positon.
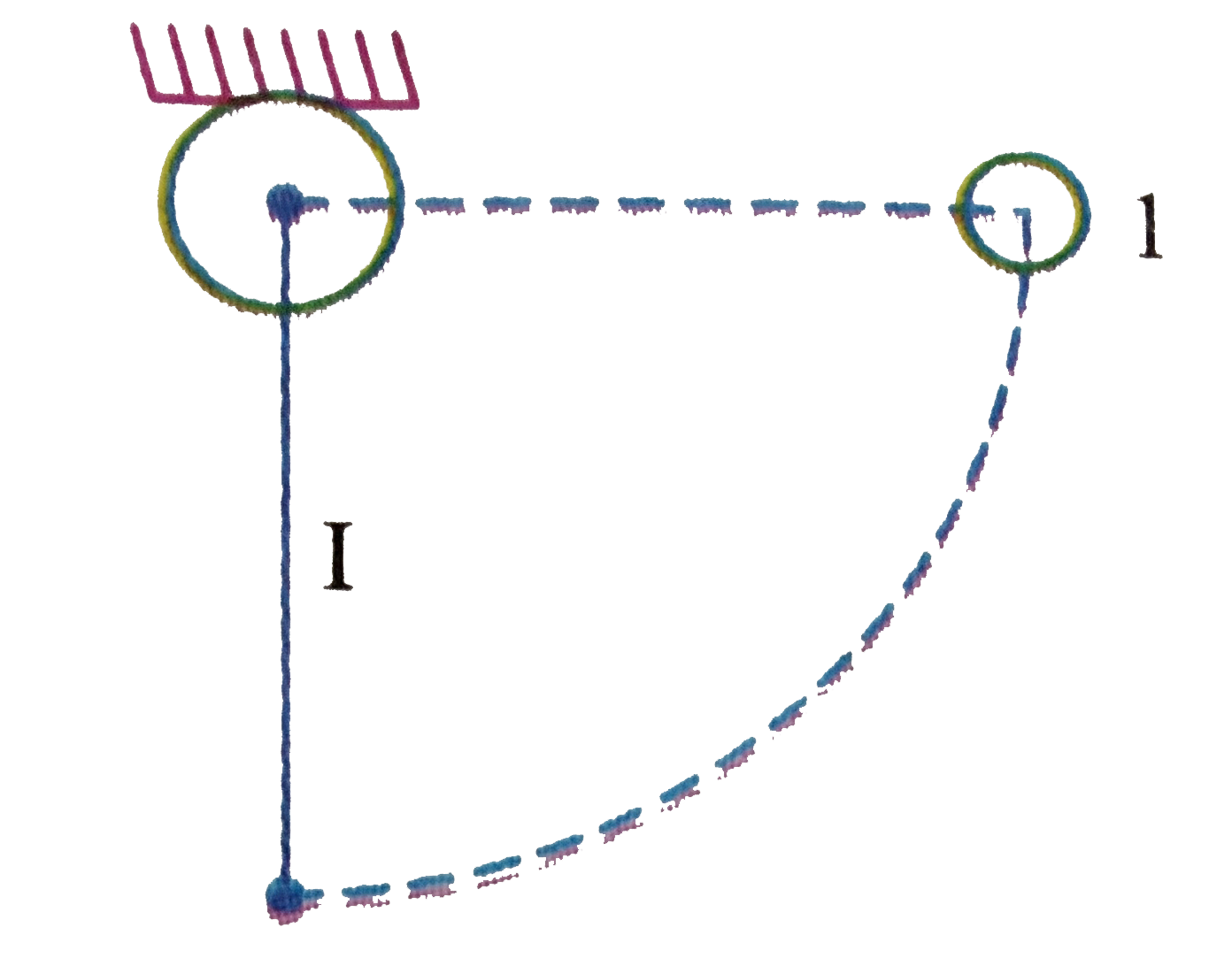
Elastic energy should in the wire in the vericle positon isA9m2g2l2Yπr2B7m2g2l2Yπr2C9m2g2lYπr2D9m2g2l4Yπr2A body of mass M is attached to the lower end of a metal wire, whose upper end is fixed . The elongation of the wire is l.
ALoss in gravitational potential energy ofM is MglBThe elastic potential energy stored in the wire is MglCThe elastic potential energy stored in the wire is 12MglDHeat produced is 12MglA wire of length 1m fixed at one end has a sphere attached to it at the other end. The sphere is projected hroizonatally with a veloicity of √9g. When it decribes a vertical circle the ratio of elongations of the wire when the sphere is at top and bottom of the circle is
A2:5B5:2C3:5D5:3
A copper wire of negligible mass, length l and corss-section A is kept on a smooth horizontal tabel with one end fiexed. A ball of mass m is attached to the other end. The wire and the ball are rotating with an angular velocity ω. If elongation in the wire is Δl, obtain the expression for the Young's modulus.
View SolutionA sphere of radius 0.1m and mass 8π kg is attached to the lower end of a steel wire of length 5.0m and diameter 10−3m. The wire is suspended from 5.22m high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is (1.994×1011N/m2).
View SolutionA body of mass M is attached to lower end of a metal wire whose upper and is fixed. The elongation is l. The ratio of loss of gravitational potential energy to the energy stored in the wire is
View SolutionA stone of mass m tied to one end of a wire of length L. the diameter of the wire is D and it is suspended vertically. The stone is now rotated in a horizontal plane and makes an angle 6 with the vertical. If Young's modulus of the wire is Y, Then the increase in the length of the wire is
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
View Solution

