A ring of radius r made of wire of density ρ is rotated about a stationary vertical axis passing through its centre and perpendicular to the plane of the ring as shown in the figure. Determine the angular velocity (in rad/s) of ring at which the ring breaks. The wire breaks at tensile stress σ. Ignore gravity. Take σ/ρ=4 and r=1m.

n=12πR√σδ
n=1πR√σδ
n=12R√σδ
n=1R√σδ
The correct Answer is:A
Let us consider small part of ring, which subtend Due to rotation, each part of ring expericence an outward force, the ring will ruputre andle θ at the center.
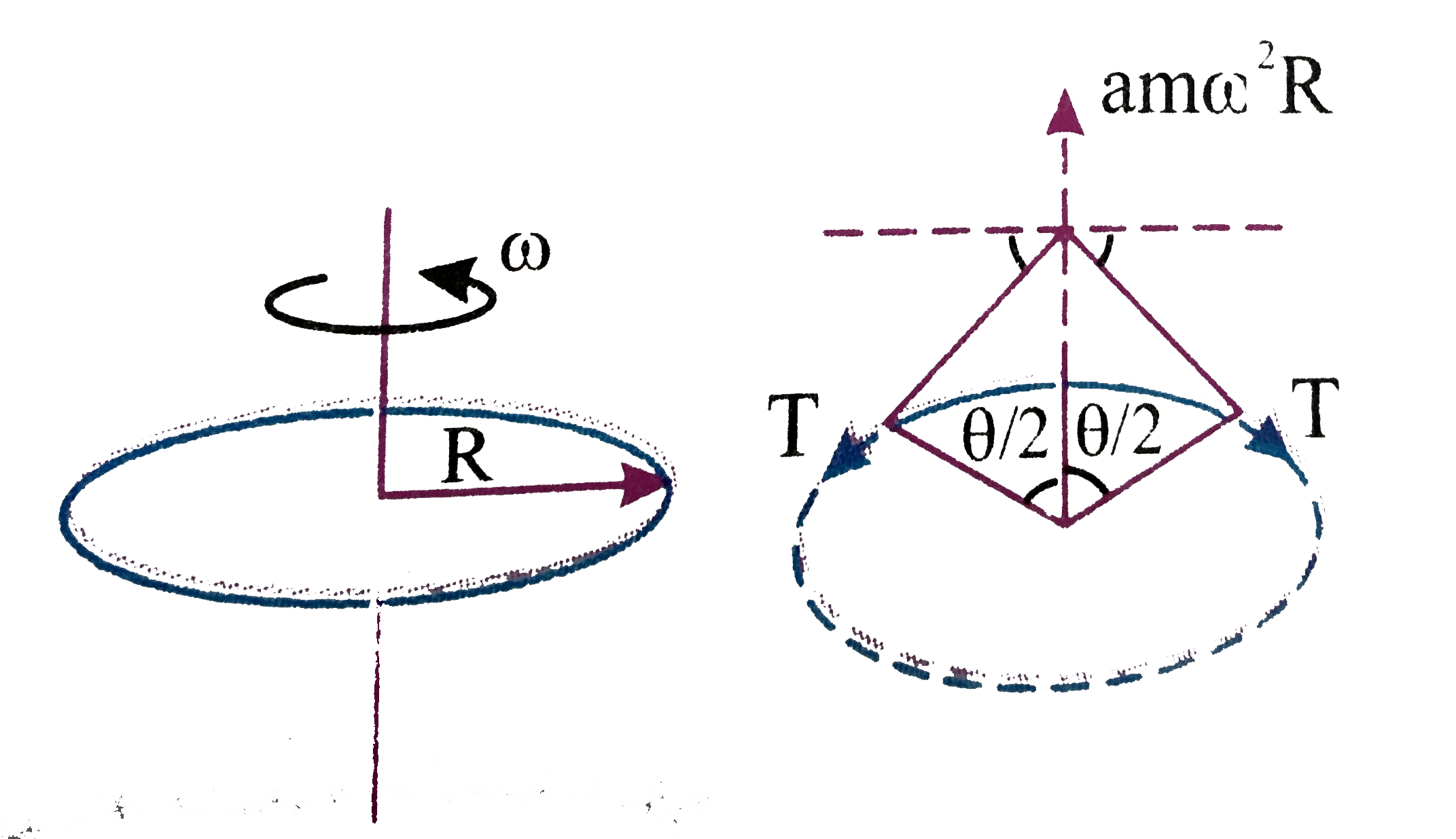
Mass fo the element (dm)=δdv=δ(ARθ)
2Tsinθ/2=(d,)ω2R
T=δω2R2 The stress at any section of the ring
⇒f=TA=δAω2R2A=δω2R2
Rupture takes place when f=σ
⇒σ=δω2R2⇒ω=√σδR2
and n=12π√ωδR2=12πR√σδ
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Comprehension-1:
Explore 2 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Comprehension-2:
Explore 2 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:COMPREHENSION TYPE
Explore 11 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:EXERCISE - III
Explore 30 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-II(H.W)
Explore 31 Videos
Similar Questions
A ring of radius r=25cm made of lead wire is rotated about a stationary vertical axis passing through its centre and perpendicular to the plane of the ring. What is the number of rps at which the ring ruptures?
View SolutionA circular ring of radius R and mass m made of a uniform wire of cross sectional area A is rotated about a stationary vertical axis passing throgh its centre and perpendicular to the plane of the ring. If the breaking stress of the material of the ring is σb, then determine the maximum angular speed ωmax at which the ring may be rotated without failure.
View Solution
Knowledge Check
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2A ring of mass 10 kg and diameter 0.4m is rotated about an axis passing through its centre and perpendicular to its plane moment of inertia of the ring is
A1.4kgm2B2.4kgm2C0.4kgm2D2kgm2A ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
A12mr2ω2Bmrω2Cmr2ω2D12mrω2
From a ring of mass M and radius R, a 30o sector is removed. The moment of inertia of the remaining portion of the ring, about an axis passing through the centre and perpendicular to the plane of the ring is
View SolutionA ring of mass 10kg and diameter 0.4m is rotated about an axis passing through its centre. If it makes 1800 revolutions per minute then , the angular momentum of the ring is
View SolutionA ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
View SolutionThe moment of inertia of a circular ring of mass 1 kg about an axis passing through its centre and perpendicular to its plane is 4 kg m2. The diameter of the ring is
View SolutionA charge q is unifomly distrybuted over a nonconducting ring of radius R. The ring is rotated about an axis passing through its centre and perpendicular to the plane of the ring with frequency f. The ratio of electric potential to the magnetic field at the centre of the ring depends on.
View Solution

