Two forces F1 and F2 are applied at the ends of a metal rod of Yougn's Modulus Y, length l as shown.
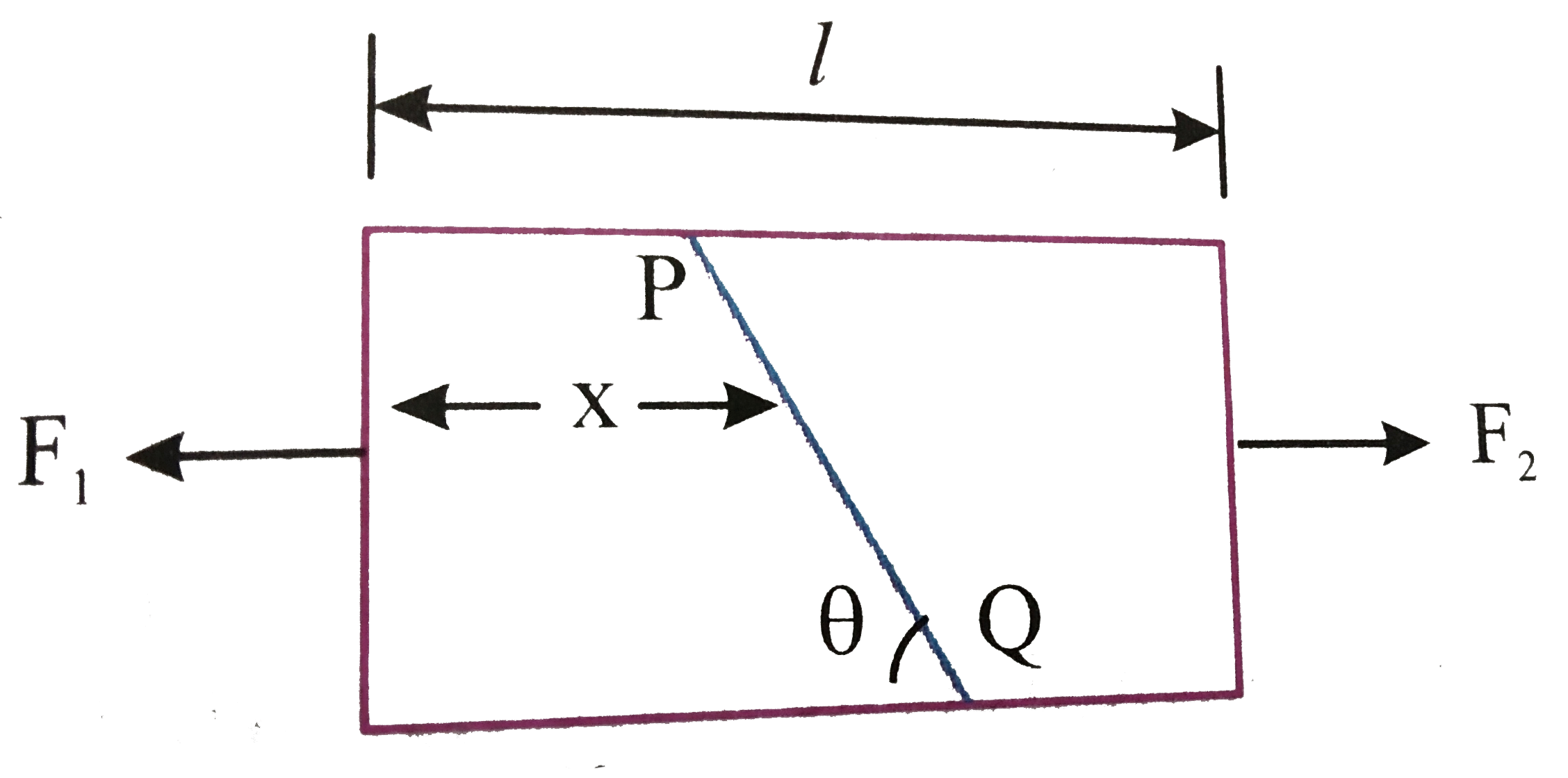
Longitudinal stress at the given cross-section PQ if the cross-section of the rod is A0 and tension is T
Tsin2θA0
TsinθcosθA0
Tcos2θA0
Tsinθcosθ2A0
The correct Answer is:B
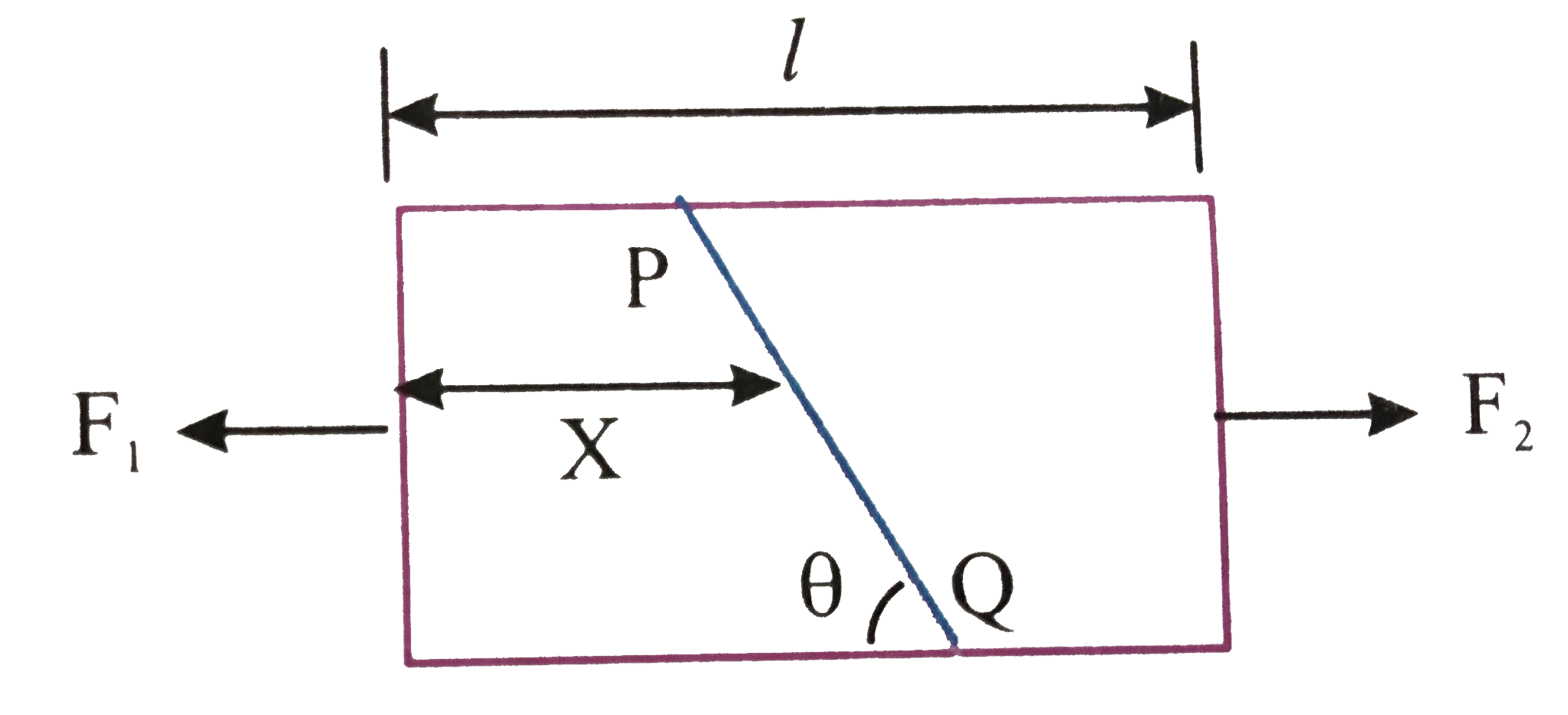
Tension at a distance x is given by
(F1−(F1−F2)xl)
Shearing stress =Tcosθa/sinθ=Tsin2θA0
where T=(F1−(F1−F2)xl)
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - SINGLE ANSWER TYPE QUESTIONS
13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Comprehension-1:
2 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - MULTIPLE ANSWER TYPE
10 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - EXERCISE - III
30 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-II(H.W)
31 Videos
Similar Questions
A homogeneous rod of length L is acted upon by two forces F1andF2 applied to its ends and directed opposite to each other. With what force F will the rod be stretched at the cross section at a distance l from the end where F1 is applied?
View SolutionTwo forces F1 and F2(F2>F1) are applied at the free ends of uniform rod kept on a horizontal frictionless surface. Find tension in rod at a distance x from end ‘A’,
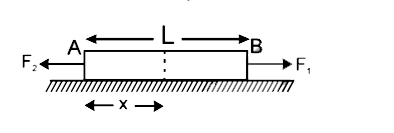
View Solution
Knowledge Check
Two equal and opposite point forces applied at mid- points of the ends of a rod of square cross shown. Consider the dotted section ABCD. If the rod is cut across this Gloss section, the force exerted by the right part of the rod on left part across this cross section is
 Aacting at point passing through cross section acting at point passing through cross section ABCDBacting at a point but not passing through the centre of cross section ABCDCuniformly distributed across the cross section ABCDDnon-uniformly distributed across the cross section ABCD
Aacting at point passing through cross section acting at point passing through cross section ABCDBacting at a point but not passing through the centre of cross section ABCDCuniformly distributed across the cross section ABCDDnon-uniformly distributed across the cross section ABCDA uniform steel rod of cross- sectional area A and L is suspended so that it hangs vertically. The stress at the middle point of the rod is
A12ρgLB14ρgLCρgLDNone of theseThe dimensions of lKA are (l is the length of rod, K is the thermal conductivity of rod and A is the area of cross-section of rod)
A[ML2T−3K−1]B[M−1L−2T3K]C[ML2T−3K−2]D[MLT−3K−1]
A force F doubles the length of wire of cross-section a The Young modulus of wire is
View Solutionon heating a cylindrical metallic rod, its length increases by 2% . Then area of cross section of rod will
View SolutionA rod of length L kept on a smooth horizontal surface is pulled along its length by a force F. The area of cross-section is A and Young's modulus is Y. The extension in the rod is

View SolutionTwo equal and opposite forces F and −F act on a rod of unifrom cross-sectional ara A, as shown in the figure. Find the (i) shearing (ii) longitual stress on the section AB.
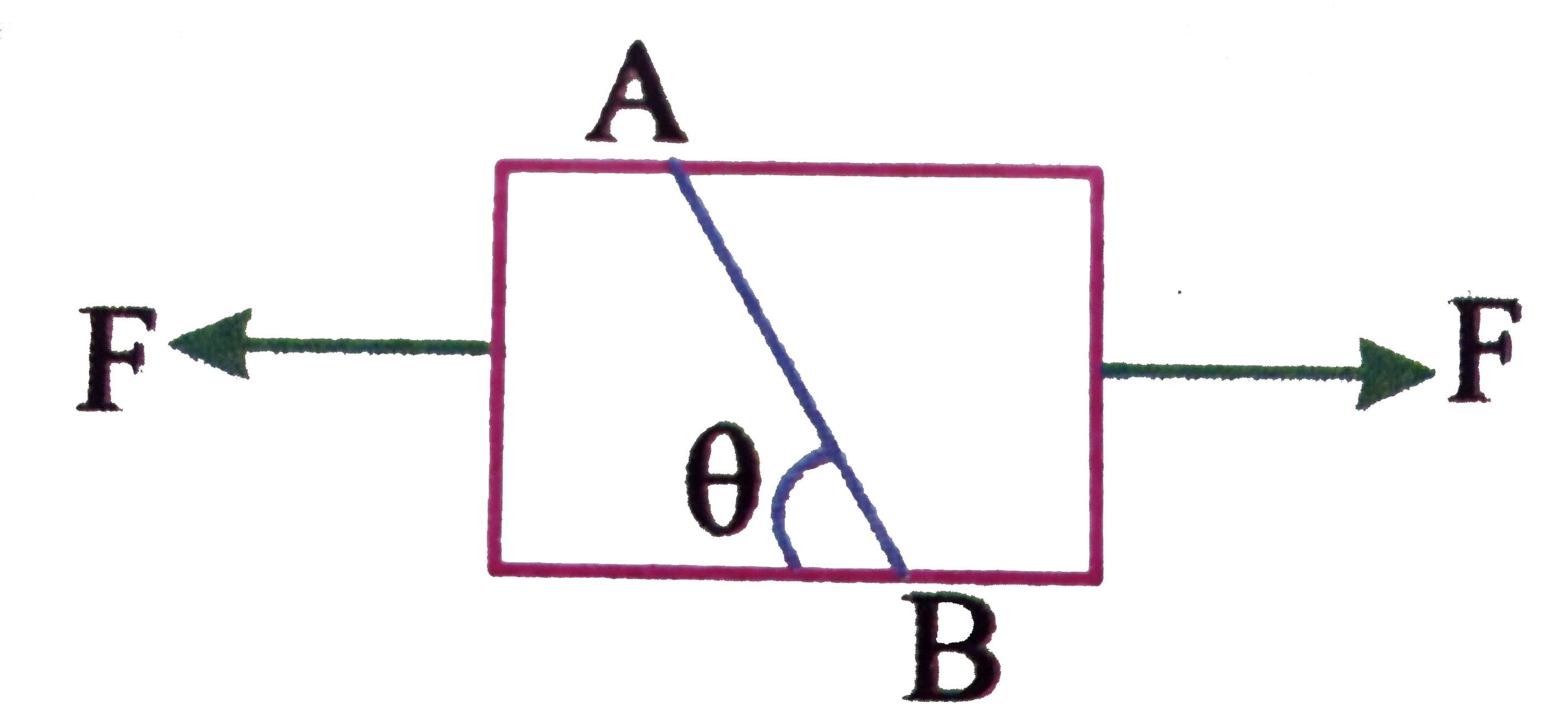
View SolutionTwo point masses of mass m and 2m placed on smooth horizontal plane are connected by a light rod of length l. Masses are given velocities in horizontal plane perpendicular to rod as shown. If area of cross section of rod is A and Young's modulus is Y, then elongation in the rod, will be
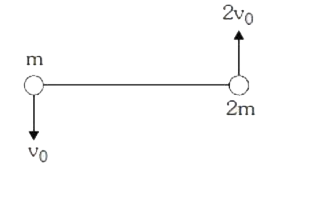
View Solution