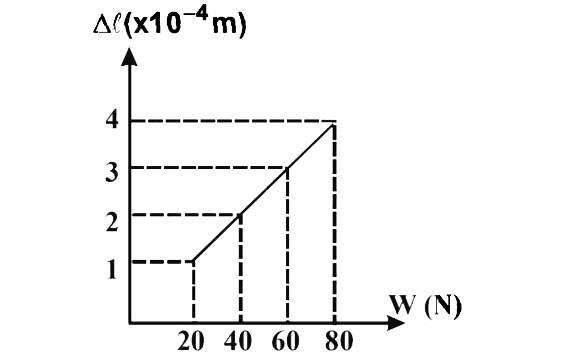
The adjacent graph shows the estension of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is , calculate the Young's modulus of the material of the wire.
The correct Answer is:A
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:MULTIPLE ANSWER TYPE
Explore 10 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:COMPREHENSION TYPE
Explore 11 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:NCERT BASED QUESTIONS
Explore 21 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:EXERCISE - III
Explore 30 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-II(H.W)
Explore 31 Videos
Similar Questions
The adjacent graph shows the extra extension (Δx) of a wire of length 1m suspended from the top of a roof at one end with an extera load Δw connected to the other end If the cross sectional area of the wire is 10−5m2 calculate the Young's modulus of the meterial of the wire
(A) 2×1011N/m2 (B) 2×10−11N/m2 (c) 3×10913)N/m3 (D) 2×1016N/m2
 .
.
View Solution_S01_065_Q01.png)
The graph shows the extension of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the young's modulus of the material of the wire is
(a). 2×1011Nm−2
(b). 2×1010Nm−2
(c). 12×1011Nm−2
(d). none of these
View Solution
Knowledge Check
The adjacent graph shows the extension Δl of a wire of length 1m, suspended from the f top of a roof at one end and with a loaf w connected to the other end. If the cross-sectional area of the wire is 106m2 calculate the young's modulus of the material of the wire .
 A2×1011Nm−2B2×10−11Nm−2C3×10−12Nm2D2×10−13Nm2
A2×1011Nm−2B2×10−11Nm−2C3×10−12Nm2D2×10−13Nm2A wire of 10m long and 1mm2 area of cross section is strechted by a force of 20N. If the elongation is 2mm the young's modulus of the material of the wire (in Pa) is
A1×109B2×10−9C1×1011D1×1012A load of 3kg produces an extension of 1.5mm in a wire of length 3m and diameter 2mm. Young's modulus of the material of the wire is
A1.87×1010Nm−2B3.5×1010Nm−2C15×1010Nm−2D2.5×1010Nm−2
The graph shown the extension of is wire of length 1 m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross sectional area of the wire is 1mm2, then the Young's modulus of the material of the wire.

View SolutionA wire of length 1 m and area of cross section 2×10−6m2 is suspended from the top of a roof at one end and a load of 20 N is applied at the other end. If the length of the wire is increased by 0.5×10−4m, calculate its Young’s modulus (in 1011N/m2).
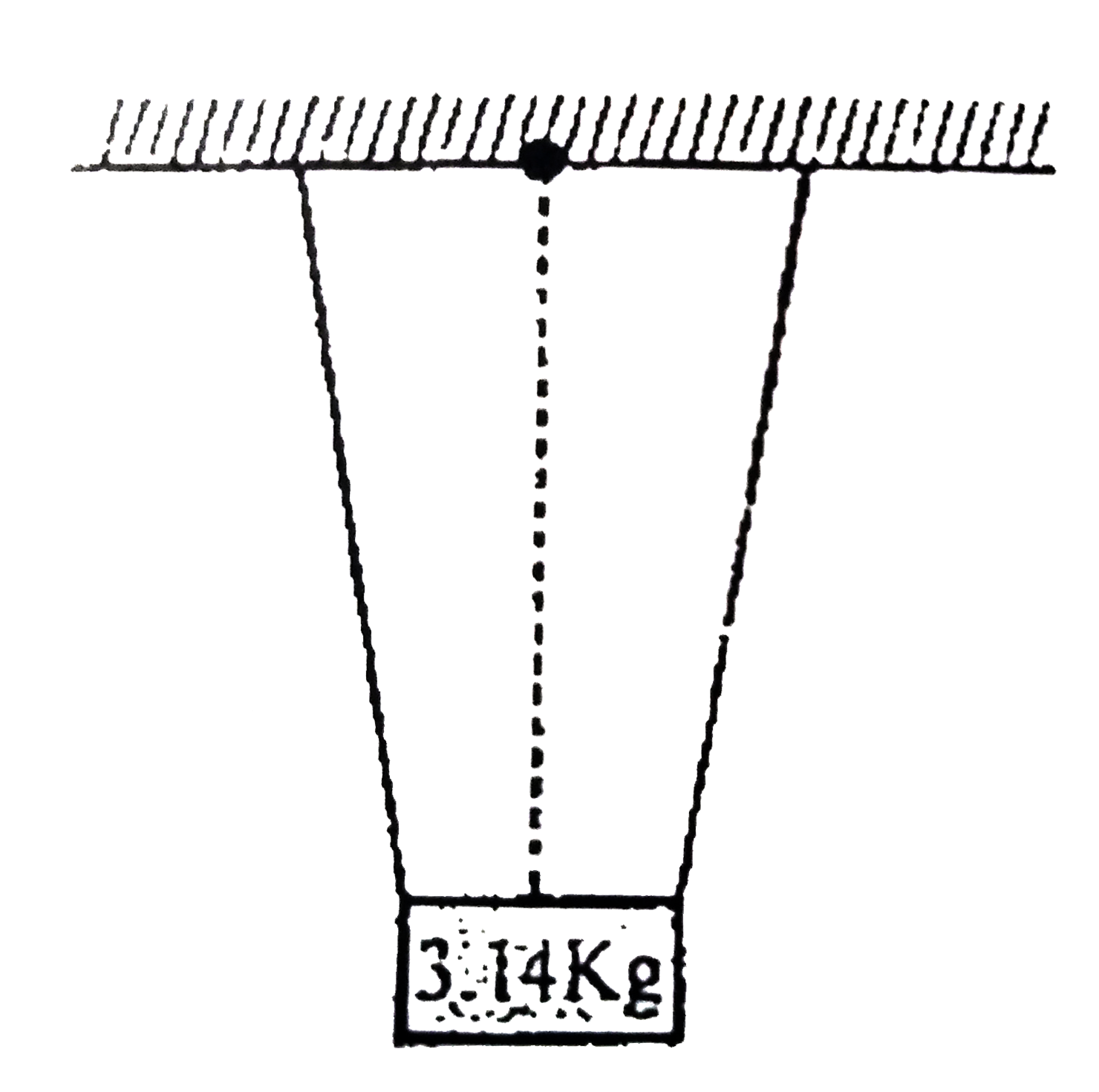
View SolutionA body of mass 3.14 kg is suspended from one end of a non uniform wire of length 10m, such that the radius of the wire is changing uniformly from 9.8×10−4 m at one end to 5×10−4 m at the other end. Find the change in length of the wire in mm. Young's modulus of the material of the wire is 2×1011N/m2 (mass of wire is negligible)
View SolutionOne end of a uniform wire of length l and weight W is attached to a point in the roof and a weight W/2 is suspended from the lower end. If A is the area fo cross-section of the wire, then stress of the wire at its midpoint will be
View SolutionA wire of mass m and length l is suspended from a ceiling. Due to its own wieght it elongates, consider cross-section are of wire as A ans Young's modulus of material of wire as Y. Th eelongation in the wire is
View Solution

