A horizongal rod fixed at one of its ends has lengtht l, rigidly modulus η and area of cross-sectional A. A bob of mass m hangs from the freee end of the rod by a light spring of stiffness constant k, Find the small displacement of the free end of the rod.

Aηmgl
mgAηl
mglAη
ηlmgA
The correct Answer is:C
The distance y fallen by the tip of the rod is given as: y=ϕl,
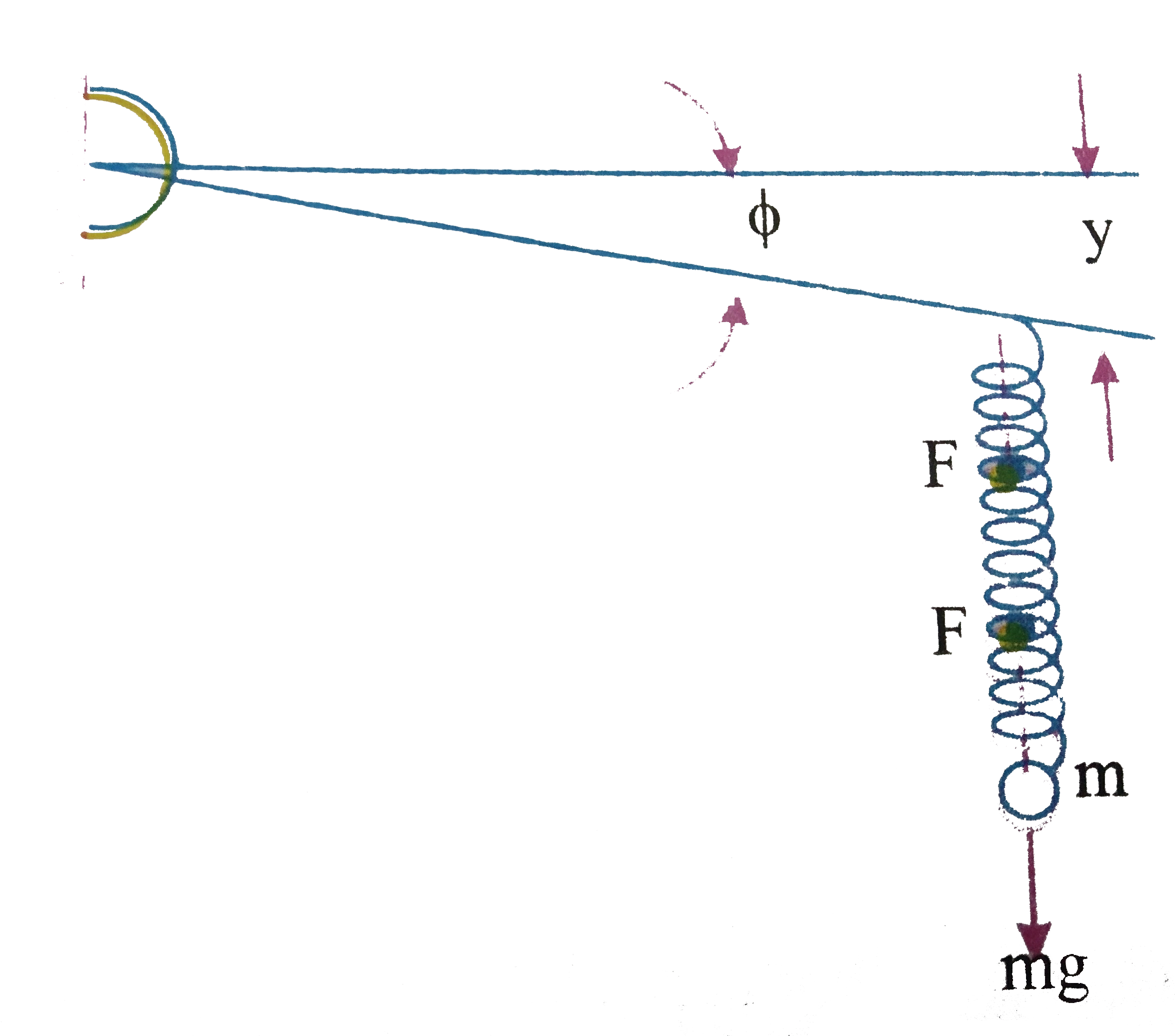
where ϕ=FAη
Then y=FlAη
Subsituing F=mg (for equilibrium of the hanging mass),
we have y=mglAη
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:MULTIPLE ANSWER TYPE
Explore 10 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:COMPREHENSION TYPE
Explore 11 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:NCERT BASED QUESTIONS
Explore 21 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:EXERCISE - III
Explore 30 Videos
- MOTION IN A PLANEBook:NARAYNAChapter:MOTION IN A PLANEExercise:Level-II(H.W)
Explore 31 Videos
Similar Questions
A rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the

Normal reaction by ground on the rod
View SolutionAB is a uniformly shaped rod of length L and cross sectional are S, but its density varies with distance from one end A of the rod as ρ=px2+c, where p and c are positive constants. Find out the distance of the centre of mass of this rod from the end A.
View Solution
Knowledge Check
A unifrom steel rod of length 1m and area of cross-section 20cm2 is hanging from a fixed support. Find the increases in the length of the rod.
A1.923×10−5cmB2.923×10−5cmC1.123×10−5cmD3.123×10−5cmA rod of mass m and length L is kept on a horizontal smooth surface. The rod is hinged at its one end A. There are two springs, perpendicular to the rod, kept in the same horizontal plane. The spring of spring constant k is rigidly attached to the lower end of rod and spring of spring constant 12k just touches the rod at its midpoint C, as shown in the figure. If the rod is slightly displaced leftward and released then, the time period for small osciallation of the rod will be
 Aπ√m3kB3π2√m3kCπ[√m3k+√3g2L]D3π2[√m3k+4√3g2L]
Aπ√m3kB3π2√m3kCπ[√m3k+√3g2L]D3π2[√m3k+4√3g2L]A wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
AMg(L1−L)ALBMgLAL1CMgLA(L1−L)DMgL1AL
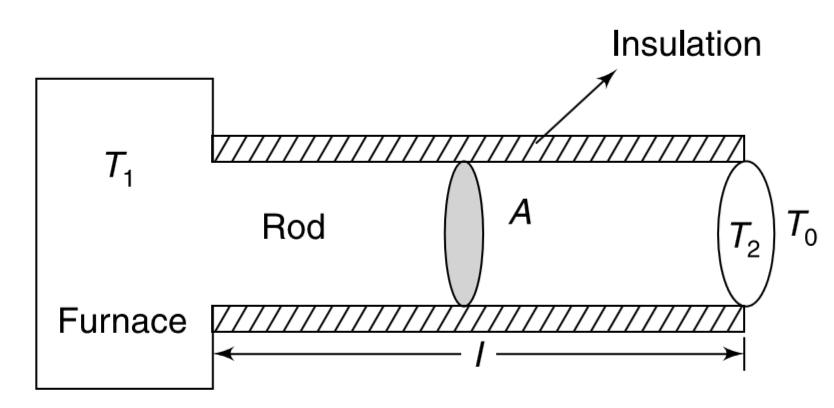
A cylindrical rod of length l, thermal conductivity k and area of cross section A has one end in a furnace maintained at constant temperature. The other end of the rod is exposed to surrounding. The curved surface of the rod is well insulated from the surrounding. The surrounding temperature is T0 and the furnace is maintained at T1=T0+ΔT1. The exposed end of the rod is found to be slightly warmer then the surrounding with its temperature maintained T2=T0+ΔT2[ΔT2<<T0]. The exposed surface of the rod has emissivity e. Prove that ΔT1 is proportional to ΔT2 and find the proportionality constant.
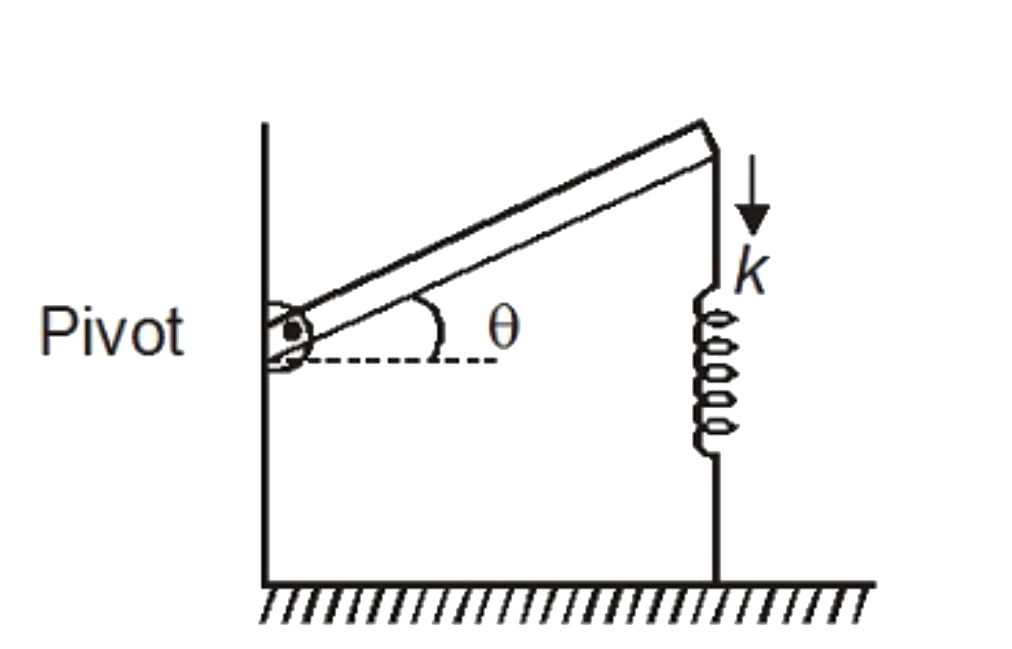
View SolutionA horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is
View SolutionA semicircular rods is joined at its end to a straight rod of the same material and the same cross-sectional area. The straight rod formss a diameter of the other rod. The junction are maintaine dat different temperature. Find the ratio of the heat transffered through a cross section of the straigh rod in a given time.
View SolutionOne end of a uniform rod of mass M and cross-sectional area A is suspended from a rigid support and an equal mass M is suspended from the other end, what is the stress at the mid point of the rod.
View SolutionA wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View Solution

