A wire of mass m and length l is suspended from a ceiling. Due to its own wieght it elongates, consider cross-section are of wire as A ans Young's modulus of material of wire as Y. Th eelongation in the wire is
2mg3YA
mglYA
mgl2YA
cannot be calcuated
The correct Answer is:C
To find the elongation in a wire of mass m and length l suspended from a ceiling due to its own weight, we can follow these steps:
Step 1: Understand the Forces Acting on the Wire
The wire is subjected to its own weight, which creates a tension that varies along its length. The weight of the wire acts downward, and the tension at any point in the wire depends on the weight of the portion of the wire below that point.
Step 2: Consider an Element of the Wire
Let’s consider a small element of the wire of length dx at a distance x from the bottom of the wire. The weight of the wire below this point contributes to the tension at this point.
Step 3: Calculate the Weight of the Wire Below the Element
The mass of the wire below the element can be expressed as:
mbelow=ml(l−x)
Thus, the weight of this portion is:
F=mbelow⋅g=ml(l−x)⋅g
Step 4: Determine the Tension in the Wire
The tension T at the point x is equal to the weight of the wire below it:
T=ml(l−x)⋅g
Step 5: Relate the Tension to the Elongation
Using the definition of Young's modulus Y:
Y=StressStrain=T/AΔL/L
Rearranging gives:
ΔL=T⋅LY⋅A
Step 6: Substitute for Tension
Substituting the expression for tension T:
ΔL=(ml(l−x)⋅g)⋅LY⋅A
Step 7: Integrate to Find Total Elongation
To find the total elongation, we need to integrate from x=0 to x=l:
ΔL=∫l0(ml(l−x)⋅g)⋅LY⋅Adx
This simplifies to:
ΔL=mgLY⋅A∫l0(l−x)ldx
Calculating the integral:
∫l0(l−x)dx=(lx−x22)l0=l2−l22=l22
Thus,
ΔL=mgLY⋅A⋅l22l=mgl2YA
Final Result
The elongation in the wire is given by:
ΔL=mgl2YA
The wire is subjected to its own weight, which creates a tension that varies along its length. The weight of the wire acts downward, and the tension at any point in the wire depends on the weight of the portion of the wire below that point.
Let’s consider a small element of the wire of length dx at a distance x from the bottom of the wire. The weight of the wire below this point contributes to the tension at this point.
The mass of the wire below the element can be expressed as:
mbelow=ml(l−x)
Thus, the weight of this portion is:
F=mbelow⋅g=ml(l−x)⋅g
The tension T at the point x is equal to the weight of the wire below it:
T=ml(l−x)⋅g
Using the definition of Young's modulus Y:
Y=StressStrain=T/AΔL/L
Rearranging gives:
ΔL=T⋅LY⋅A
Substituting the expression for tension T:
ΔL=(ml(l−x)⋅g)⋅LY⋅A
To find the total elongation, we need to integrate from x=0 to x=l:
ΔL=∫l0(ml(l−x)⋅g)⋅LY⋅Adx
This simplifies to:
ΔL=mgLY⋅A∫l0(l−x)ldx
Calculating the integral:
∫l0(l−x)dx=(lx−x22)l0=l2−l22=l22
Thus,
ΔL=mgLY⋅A⋅l22l=mgl2YA
The elongation in the wire is given by:
ΔL=mgl2YA
Topper's Solved these Questions
Similar Questions
A wire of length L and cross sectional area A is made of a material of Young's modulus Y. If the wire is streched by an amount x, the work done is………………
View SolutionA wire of length L and cross sectional area A is made of a material of Young's modulus Y. If the wire is stretched by an amount x, the work done is :
View Solution
Knowledge Check
To determine Young's modulus of the material of a wire,
Atwo wires of same length and radius are takenBSingle straight wire of uniform cross section is takenCthree wires of different lengths but of same material are takenDtwo springs of same length but different materials are takenConsider a wire of length L, density ρ and Young's modulus Y . If l is elongation in wire, then frequency of wire is
A12L√YlρLB12L√YLρlC1L√YLρlD1L√YlρLA wire of length L and cross sectional area A is made of a material of Young's modulus Y. If the wire is stretched by an amount x, the work done is :
AYALxBYALx2CYA2LxDYA2Lx2
A block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View SolutionA wire of length L and cross-sectional area A is made of material of Young's modulus Y. The work done in stretching the wire by an amount x is
View SolutionA mass (m) is suspended at the end of a weightless wire of length L, cross-sectional area A and Young's modulus Y. The period of oscillation for the S.H.M. along the vertical direction is
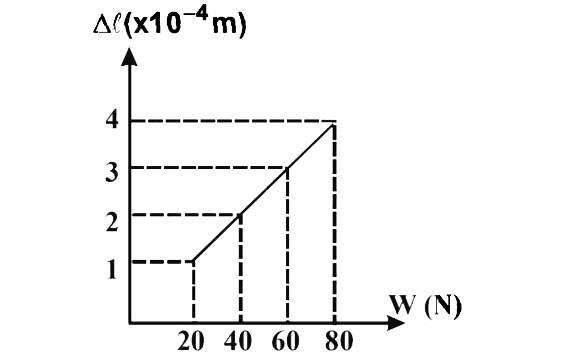
View SolutionThe adjacent graph shows the estension (Δl) of a wire of length 1m suspended from the top of a roof at one end and with a load W connected to the other end. If the cross-sectional area of the wire is 10−6m2, calculate the Young's modulus of the material of the wire.
View SolutionIf the length of a wire is doubled, then its Young's modulus
View Solution

