The free end of a thread wound on a bobbin is passed round a nail A hammered into the wall. The thread is pulled at a constant velocity 'v' . Assuming pure rolling of bobin, find the velocity of the centre of the bobbin at the instant when the thread forms an angle with the vertical: ( and are outer and inner radii off the babbin)

The correct Answer is:A
When the thread is pulled, the bobbin rolls to the right. Resultant velocity of point along the thread is , where is the and linear velocity due to rotation. As the bobbin rolls without slipping, . solving the obtained equations, we get
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
The point P of a string is pulled up with an acceleration g. Then the acceleration of the hanging disc (w.r.t ground) over which the string is wrapped, is
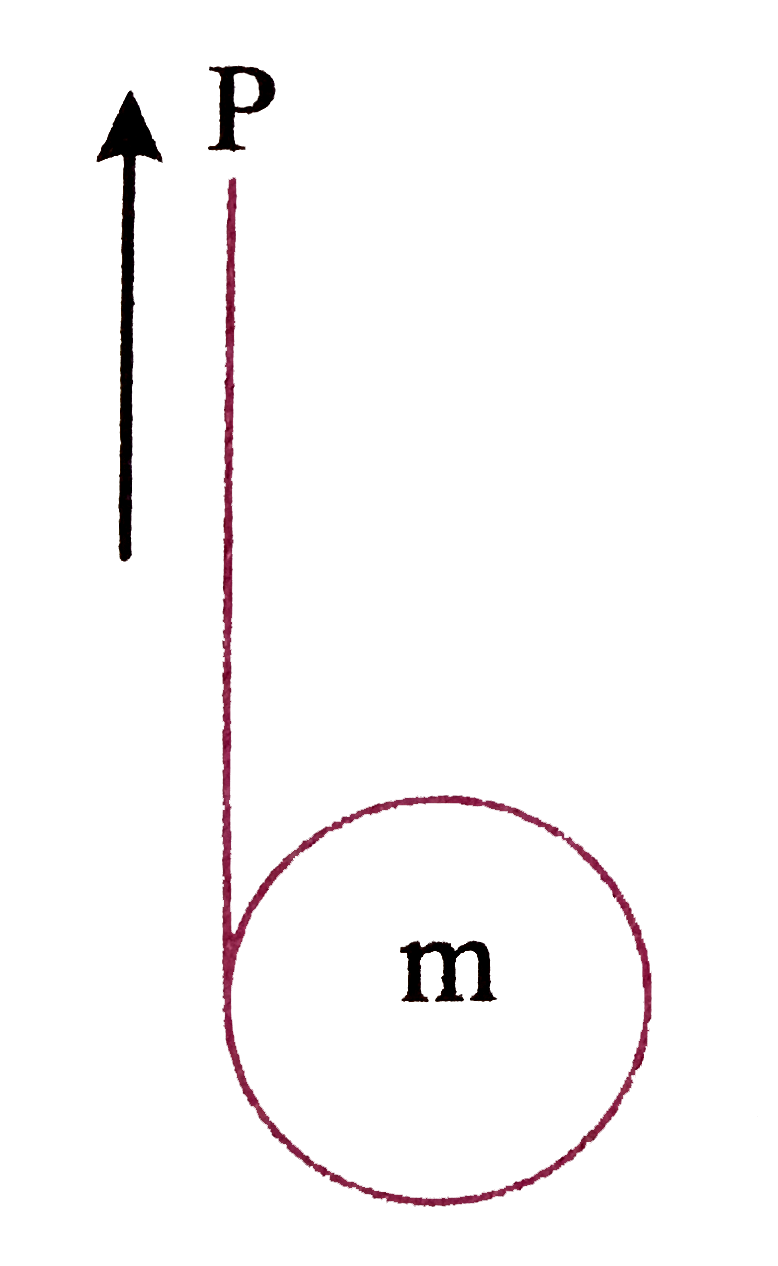
View SolutionFour particles, each of mass 1kg are placed at the corners of a square of side 1m in the XY plane. If the point of intersecting of the diagonals of the square is taken as the origin, the co-ordinates fo the centre of mass are
View SolutionWhat is the discovery of CV Raman?
View SolutionFor which of the following does the centre of mass lie outside the body ?
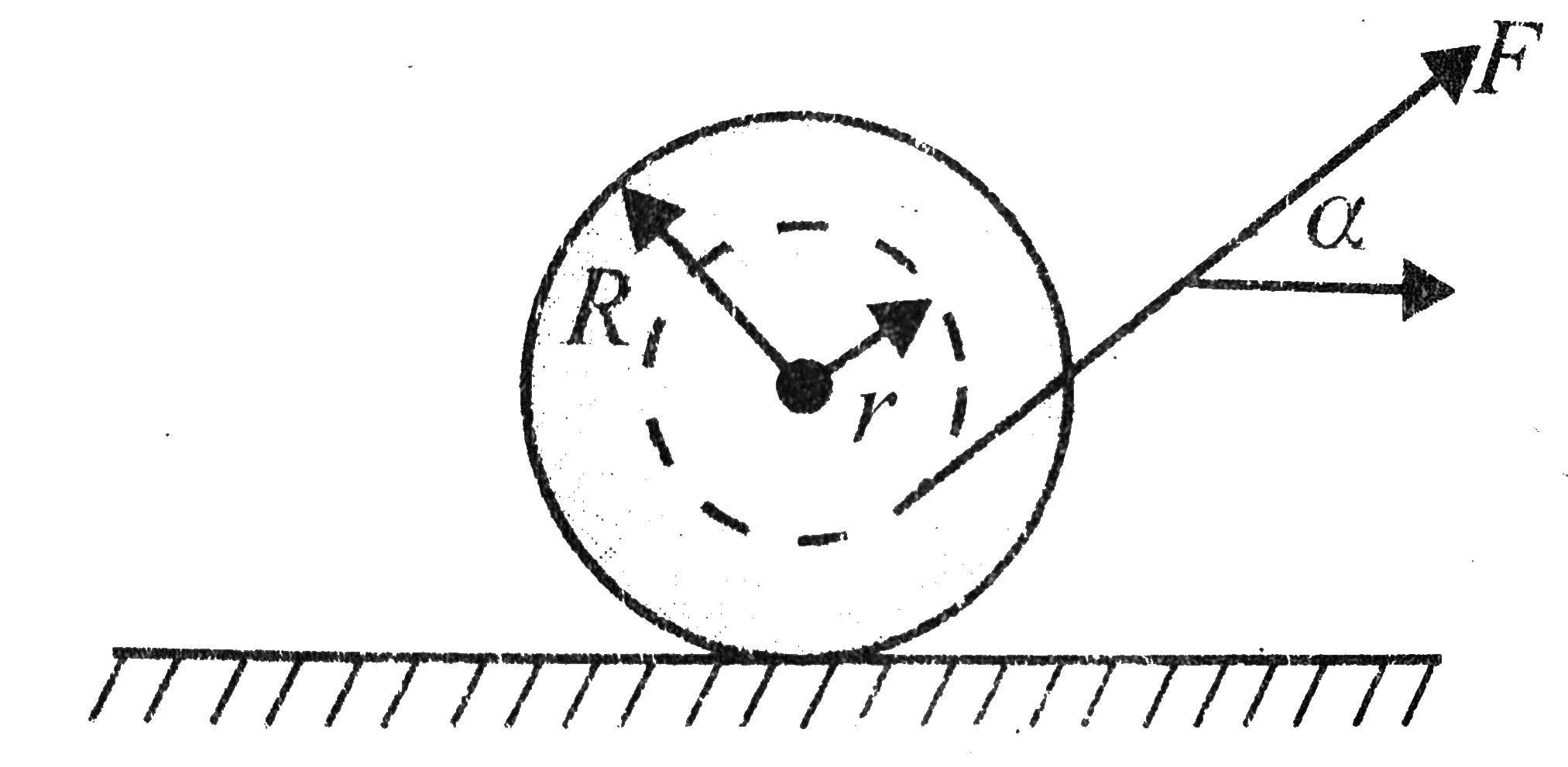
View SolutionInner and outer radii of a spool are r and RI, respectively. A thread is wound over its inner surface and spool is placed over a rough horizontal surface. Thread is pulled by a force F as shown in Fig. In case of pure rolling, which of the following statements are false?
View SolutionA uniform cylinder of mass m rests on two rough horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F
View SolutionInner and outer radii of a spool are r and R respectively. A thread is wound over its inner surface and placed over a rough horizontal surface. Then: .
View SolutionA spool of inner radius R and outer radius 3R has a moment of inertia =MR2 about an axis passing through it's geometric centre, where M is the mass of the spool. A thread wound on the inner surface of the spool is pulled horizontally with a constant force =Mg. Find the acceleration of the point on which is being pulled assuming that the spool rolls purely on the floor.
 .
.
View SolutionA small sphere of mass m suspended by a thread is first taken aside so that the thread forms the right angle with the vertical and then released. Find: (a) the total acceleration of the sphere and the thread tension as a function of theta , the angle of deflection of the thread from the vertical, (b) the thread tension at the moment when the vertical component of the sphere's velocity is maximum, (c) the angle theta between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally.
View SolutionA closed chian A of mass m=0.36kg is attached to a vertical rotating shaft by means of a thread (figuer), and rotates with a constant angular velocity ω=35rad/s. The thread forms an angle θ=45∘ with the vertical. Find the distance between the chain's of the thread.

View SolutionA small body of mass m tied to a non-stretchable thread moves over a smooth horizontal plane. The other end of the thread is being drawn into a hole O(figure) with a constant velocity. Find the thread tension as a function of the distance r between the body and the hole if at r=r0 the angular velocity of the thread is equal to ω0.
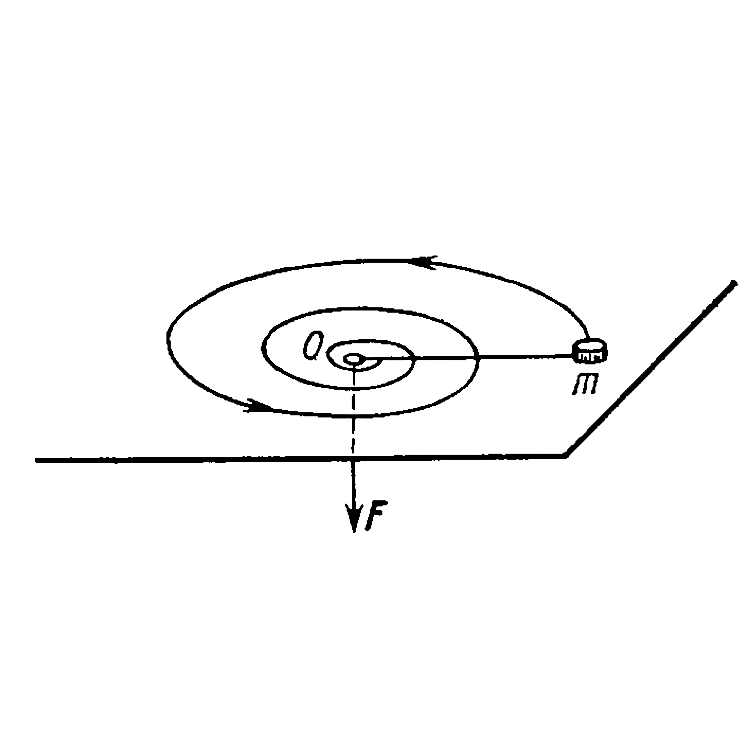
View SolutionA closed chain A of mass m = 0.36kg is attached to a vertical rotating shaft by means of thread showin in fig. and rotated with a constant angular velocity omega=35rad//s . The thread forms an angle theta=45^(@) with the vertical. Then the tension of the thread is
View SolutionIn the arrangement shown in the fig, end A of the string is being pulled with a constant horizontal velocity of 6 m//s . The block is free to slide on the horizontal surface and all string segments are horizontal. Find the velocity of point P on the thread.
View SolutionBelow the fixed end O of the insulating horizontal thread OB, there is a fixed charge A of Q = 20muc . At the end B of the thread there is a small mass m carrying charge Q = 20moc . The mass is released from the position shown and it is found to come to rest when the thread becomes vertical. Assume that the thread does not hit the fixed charge at A. [g = 10 m//s^2] (a) Find mass m. (b) Find tension in the thread in the equilibrium position when the thread is vertical. (c) Is the equilibrium mentioned in (b) stable or unstable?
View SolutionA bobbin rolls without slipping over a horizontal surface so that the velocity v of the end of the thread (point A) is directed along the horizontal . A board hinged at point B leans against the bobbin (Fig.) The inner and outer radii of the bobbin are r and R respectively. Determine the angular velocity ω of teh board as a function of an angle α.

View SolutionA ball is tied by a weightless inextensible thread to a fixed cylinder of radius r. At the initial moment the thread is wound so that the ball touches the cylinder. Then the ball acquires a velocity v in the raidal direction, and the thread starts unwinding (Fig). Determine the length l of the upwound segment of the thread by the instant of time t, neglecting the force of gravity.
View Solution

