Question

A spool of inner radius $R$ and outer radius $3R$ has a moment of inertia $=M{R}^2$ about an axis passing through it's geometric centre, where $M$ is the mass of the spool. A thread wound on the inner surface of the spool is pulled horizontally with a constant force $=Mg$. Find the acceleration of the point on which is being pulled assuming that the spool rolls purely on the floor.
.

Answer

`16 m//s^(2)`

Explanation

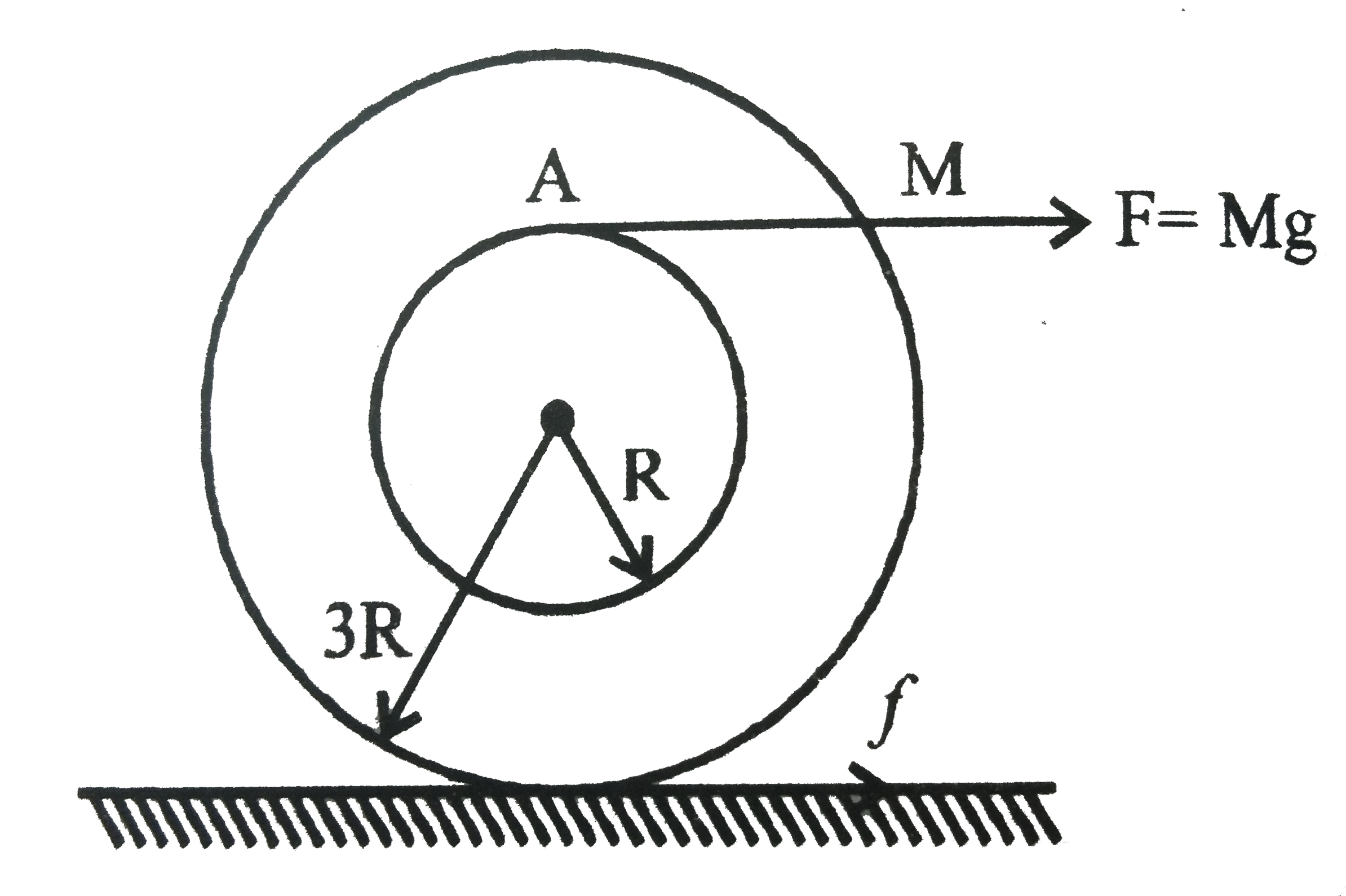
for translation motion `F + f = Ma` ….(1)
for rotational motion
`F xx R -f xx 3R = I alpha rArr R(F-3f) = (MR^(2)) alpha`
`F -3f =(M)/(2) (3R alpha) rArr F-3f = (Ma)/(3)`….(2)
Solving (1) and (2) we get
`a = (6g)/(5)` & `alpha = (2g)/(5R)`
now `a_(A) = a + R alpha`
`a_(A) = (6g)/(5) + (2g)/(5)`
`a_(A) =(8g)/(5) rArr a_(A) = 16 m//s^(2)`.