μ is coefficient of friction between all surface. Block A is kept of over block B on inclined plane. The minimum force required such that 'A' block can accelerate along applied force is mgsinθ+nμgcosθ calculate n.
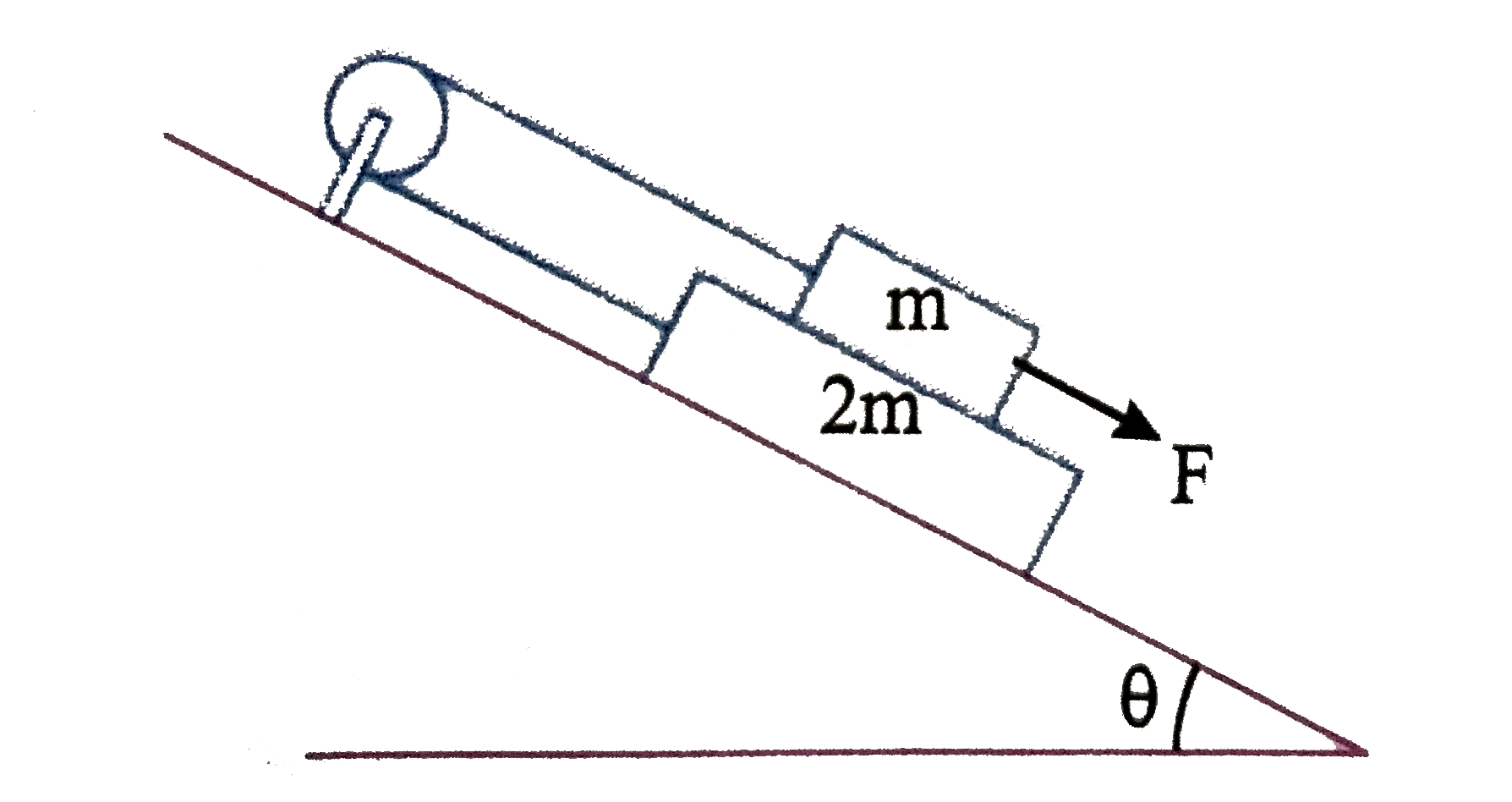
The correct Answer is:5
Frictional force developed in all surface is limiting
F+3mgsinθ+3μmgcosθ=2T …(i)
T−2mgsinθ−3μmgcosθ−μmgcosθ=0
T=2mgsinθ+4μmgcosθ ….(ii)
Solving the equation
F=mgsinθ+5μmgcosθ
Topper's Solved these Questions
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions I
Explore 6 Videos
- FRICTIONBook:NARAYNAChapter:FRICTIONExercise:Passage type of questions
Explore 6 Videos
- COLLISIONBook:NARAYNAChapter:COLLISIONExercise:Level-II (H.W)
Explore 54 Videos
- GRAVITATIONBook:NARAYNAChapter:GRAVITATIONExercise:EXERCISE -IV
Explore 40 Videos
Similar Questions
μ is coefficient of friction between all surfaces . Block A is kept over block B on inclined plane . The minimum force required such that 'A' block can accelerate along applied force is mg sin θ+nμgcosθ , calculate n .

View SolutionThe coefficient of friction between the block and the inclined plane is μ.
View Solution
Knowledge Check
In the arrangement shown in figure coefficient of friction between 5kg block and incline plane is μ=0.5. Friction force acting on the 5kg block is
 A20NB15NC10ND5N
A20NB15NC10ND5NA block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θA block of mass m is placed on a rough inclined plane. The coefficient of friction between the block and the plane is μ and the inclination of the plane is θ. Initially theat−0 and the block will certain stationary on the plane. Now the inclination θ is gradually increased. The block presses the inclined plane with a force mgcosθ. So welding strength between the block and inclined is μmgcosθ, and the pulling forces is mgsinθ. As soon as the pulling force is greater than the welding strength, the welding breaks and the block starts sliding, the angle θ for which the block starts sliding is called angle of repose (λ). During the contact, two contact forces are acting between the block and the inclined plane. The pressing reaction (Normal reaction) and the shear reaction ( frictional force) and the shear reaction (frictional force) . The net contact force will be resultant of both.

If the entire system, were accelerated upward with acceleration 'a', the angle of repose , would :AincreasesBdecreasesCremain sameDincrease of a>g
A block of weight 1 N rests on a inclined plane of inclination θ with the horizontal. The coefficient of friction between the block and the inclined plane is μ. The minimum force that has to be applied parallel to the inclined plane to make the body just move up the plane is
View SolutionA 2kg block is in contact with a vertical wall having coefficient of friction 0.5 between the surfaces. A horizontal force of 40N is applied on the block at right angles to the wall. Another force of 15N is applied on the plane of the wall and at right angles to 40N force. Find the acclecration of the block .
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionBlock A has a mass of 30kg and block B a mass of 15kg . The coefficient of friction between all surface of contact are μs=0.15 and μs=0.10 Knowing that θ=30∘ and that the magnitude of the force F applied to block A is 250N Determine (a) acceleration of block A and (b) the tension in the rope

View SolutionTwo blocks A and B are lying on the table as shown in the figure. The coefficient of friciton between block A and block B is μ. The coefficient of friction between block B and ground also μ. An external force F is applied in the direction shown. The maximum value of the force F that can be applied without moving the blocks.
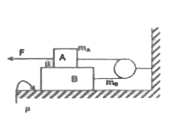
View Solution

