A 2kg block is in contact with a vertical wall having coefficient of friction 0.5 between the surfaces. A horizontal force of 40N is applied on the block at right angles to the wall. Another force of 15N is applied on the plane of the wall and at right angles to 40N force. Find the acclecration of the block .
To solve the problem of finding the acceleration of the block, we can follow these steps:
Step 1: Identify the forces acting on the block
- The block has a weight acting downwards, which can be calculated as:
W=m⋅g=2kg⋅9.8m/s2=19.6N
- There is a horizontal force of F1=40N acting on the block towards the wall.
- There is another force F2=15N acting perpendicular to F1.
Step 2: Calculate the frictional force
- The frictional force Ff can be calculated using the coefficient of friction μ and the normal force N. The normal force in this case is equal to the horizontal force applied:
Ff=μ⋅N=0.5⋅40N=20N
Step 3: Determine the net force acting on the block
- The net force Fnet acting on the block can be calculated by considering the vertical and horizontal components of the forces. The weight acts downwards, and the frictional force acts in the opposite direction to the applied force F2:
Fnet=F2−Ff=15N−20N=−5N
- Since the frictional force is greater than the applied force F2, the block will not move in the direction of F2.
Step 4: Calculate the acceleration
- Since the net force is negative, it indicates that the frictional force is preventing the block from accelerating in the direction of F2. Therefore, the acceleration a can be calculated using Newton's second law:
a=Fnetm=−5N2kg=−2.5m/s2
- The negative sign indicates that the block is not accelerating in the direction of the applied force F2.
Conclusion
The acceleration of the block is 0m/s2 because the frictional force is sufficient to counteract the applied force F2.
- The block has a weight acting downwards, which can be calculated as:
W=m⋅g=2kg⋅9.8m/s2=19.6N
- There is a horizontal force of F1=40N acting on the block towards the wall.
- There is another force F2=15N acting perpendicular to F1.
- The frictional force Ff can be calculated using the coefficient of friction μ and the normal force N. The normal force in this case is equal to the horizontal force applied:
Ff=μ⋅N=0.5⋅40N=20N
- The net force Fnet acting on the block can be calculated by considering the vertical and horizontal components of the forces. The weight acts downwards, and the frictional force acts in the opposite direction to the applied force F2:
Fnet=F2−Ff=15N−20N=−5N
- Since the frictional force is greater than the applied force F2, the block will not move in the direction of F2.
- Since the net force is negative, it indicates that the frictional force is preventing the block from accelerating in the direction of F2. Therefore, the acceleration a can be calculated using Newton's second law:
a=Fnetm=−5N2kg=−2.5m/s2
- The negative sign indicates that the block is not accelerating in the direction of the applied force F2.
The acceleration of the block is 0m/s2 because the frictional force is sufficient to counteract the applied force F2.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - C.U.Q
73 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - LEVEL -I (C.W)
47 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W
29 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - EXERCISE - IV
41 Videos
Similar Questions
A block of mass 2 kg is pushed against a rough vertical wall with a force os 40 N. Coefficient of static friction being 05. Another horizontal force is 15 N, is applied on the block in a direction paralle to the wall. Will the block move? If yes in which direction? If no, find the frictional force exerted by the wall on the block.
View SolutionA block of weight 5N is pushed against a vertical wall by a force 12 N. The coefficient of friction between the wall and block is 0.6. The magnitude of the force exerted by the wall on the block is
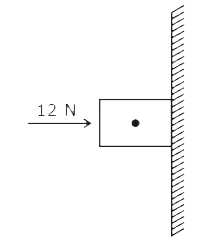
View Solution
Knowledge Check
A block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
A8.8NB5.8NC2.8ND10.8NA block of mass 5kg is lying on a rough horizontal surface. The coefficient of static and kinetic friction are 0.3 and 0.1 and 10m/s−2. If a horizontal force of 50N is applied on the block, the frictional force is
A25NB5NC10NDZeroA block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a force of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
A32 NB18 NC19 ND9.8 N
A 3kg block is placed over a 10kg block and both are placed on a smooth horizontal surface. The coefficient of friction between the blocks is 0.2. IF a horizontal force of 20N is applied to 3kg block. Find the acceleration of the two blocks.
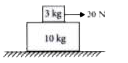
View SolutionA block of mass m=4kg is placed over a rough inclined plane as shown in fig . The coefficient of friction between the block and the plane μ=0.5 A force F=10N is applied on the block at an angle of 30∘. Find the contact force between the block and the plane.
k

View SolutionA block of weight 5 N is pushed against a vertical wall by a force 12 N . The coefficient of friction between the wall and block is 0.6 . Find the magnitude of the force exerted by the wall on the block :

View SolutionA horizontal force of 10N is necessary to just hold a block stationary against as well. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
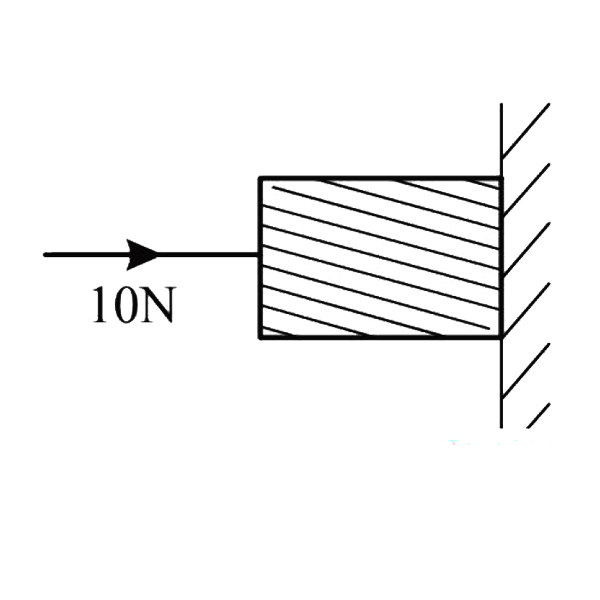
View SolutionA rectangular block of mass 5 kg is kept on a horizontal surface . The coefficient of friction between the block and the surface is 0.2 . If a force of 20 N is applied to the block at angle of 30∘ with the horizontal plane , what is the force of friction on the block ? (Take g = 10m/s2)
View Solution