In the shown P1 and P2 are massless pulleys P1 is fixed and P2 can move Masses of A,B and C are 9m642m amd m respectively All contacts are smooth and the string is massless θ=tan−1(34) (Take g=10m/s2)
The tension in string connecting pulley P2 and block C is 13x Calculate x (Take m=1kg)
 .
.
The correct Answer is:2
N1(35)=mA.aA→(1)mBg−T−45N1=mBαB→(2)
2T−mCg=mCaC→(3)aB=34aA→(4)
aB=2aC→(5) after solving above equations we get
aA=8/sec2,aB=6m/sec2,aC=3m/sec2,T=132N
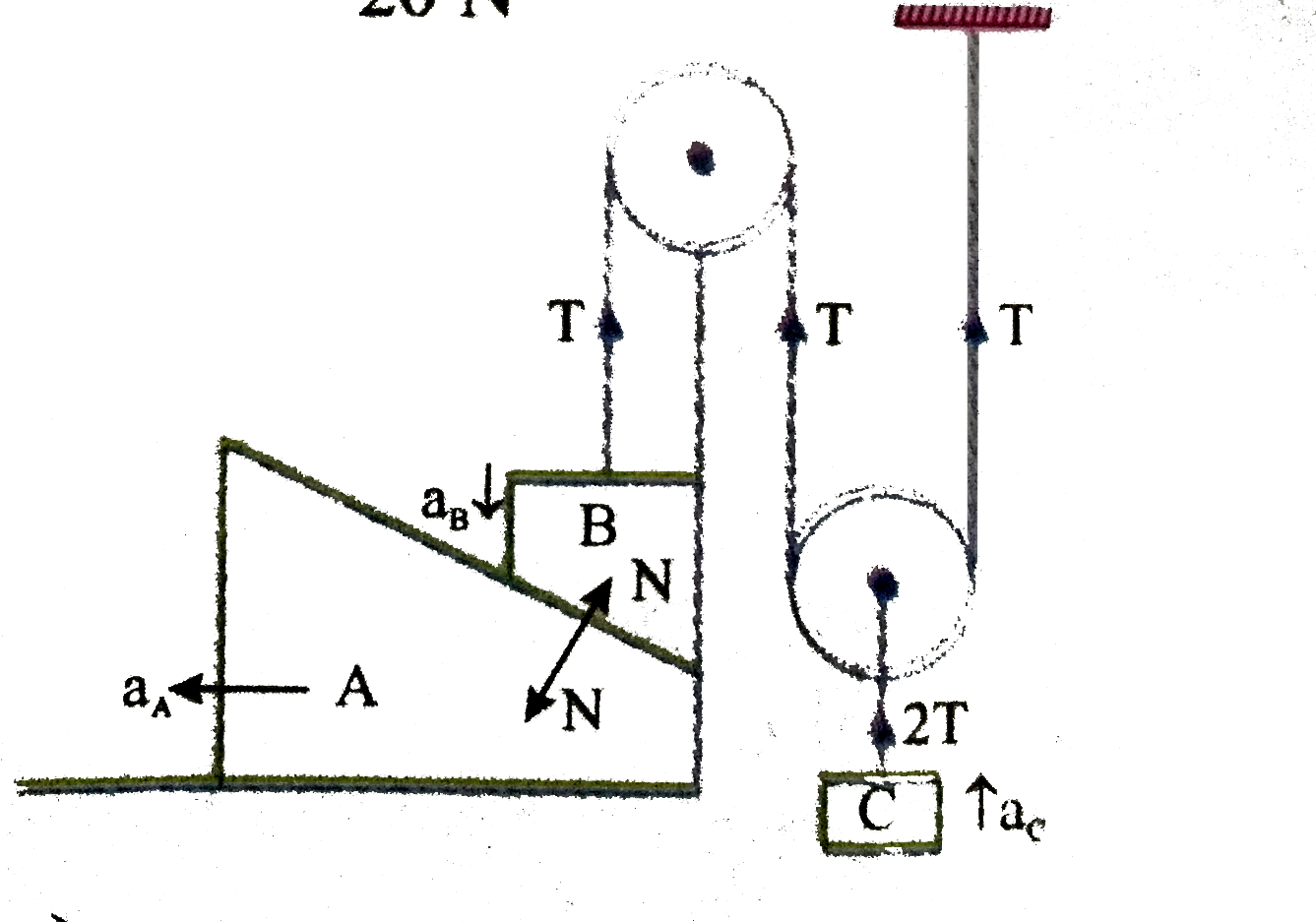 .
.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:MULTIPLE ANSWER QUESTIONS
Explore 9 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:SINGLE ANSWER QUESTIONS Passage -1
Explore 1 Video
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - IV
Explore 41 Videos
Similar Questions
If pulley is ideal and string is massless then reading of weighing machine is 5x3kg then calculate x.:(g=10m/s2)

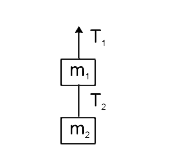
View SolutionTwo blocks with masses m1=0.2 kg and m2=0.3 kg hang one under other as shown in figure. Find the tensions in the strings (massless) in the following situations :
(g=10m/s2)
they move upward at 5 m/s
View Solution
Knowledge Check
In the arrangement shown in the all contact surfaces are smooth strings and pulleys are massless
Given M1=1kg,M2=2kg,M3=4kg and g=10ms−2
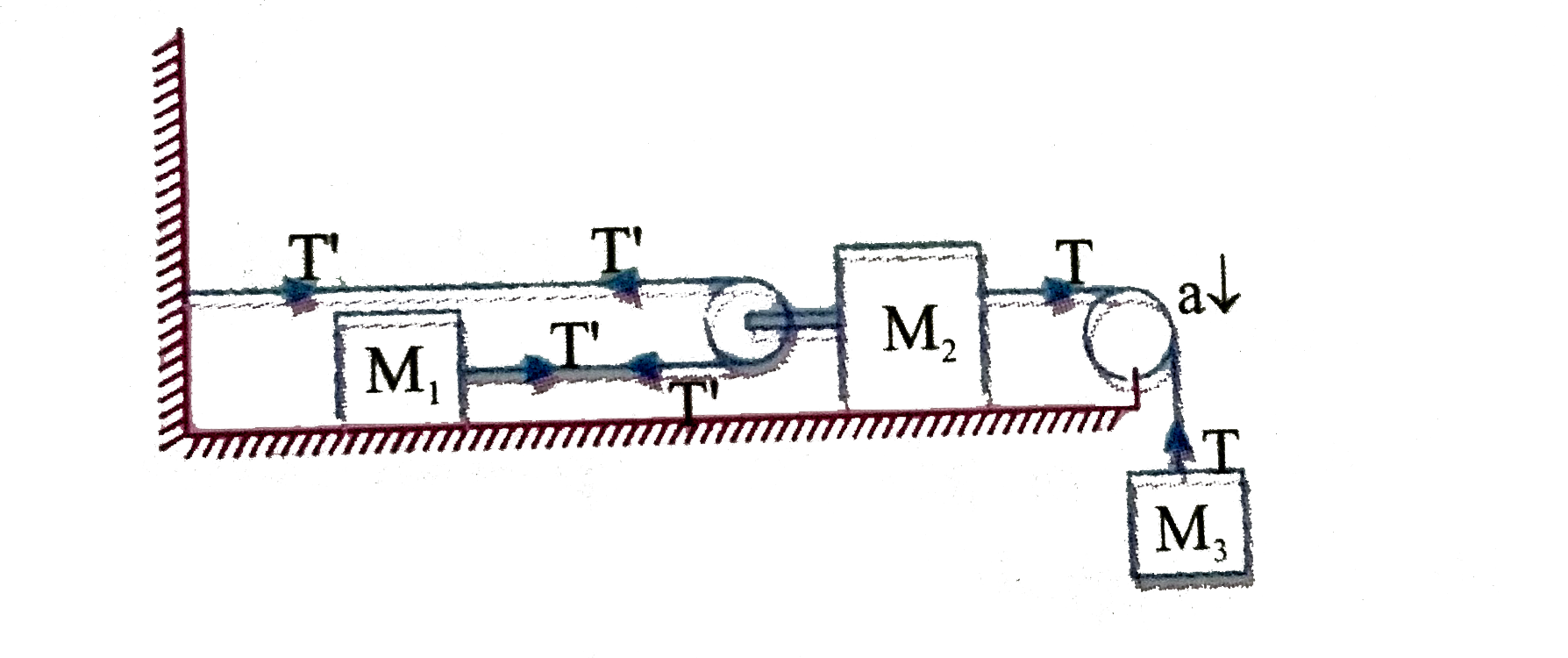 .AThe acceleration of block of mass M3 is 4ms−2BThe acceleration of block of mass M1 is 4ms−2CThe tension (T) in the string connecting blocks of masses M3 and M2 is 24N .DThe tension (T) in the string connecting blocks of masses M1 and M2 is 24N .
.AThe acceleration of block of mass M3 is 4ms−2BThe acceleration of block of mass M1 is 4ms−2CThe tension (T) in the string connecting blocks of masses M3 and M2 is 24N .DThe tension (T) in the string connecting blocks of masses M1 and M2 is 24N .In the figure, pulleys are smooth and strings are massless, m1=1 kg and m2=13kg. To keep m3 at rest, mass m3 should be
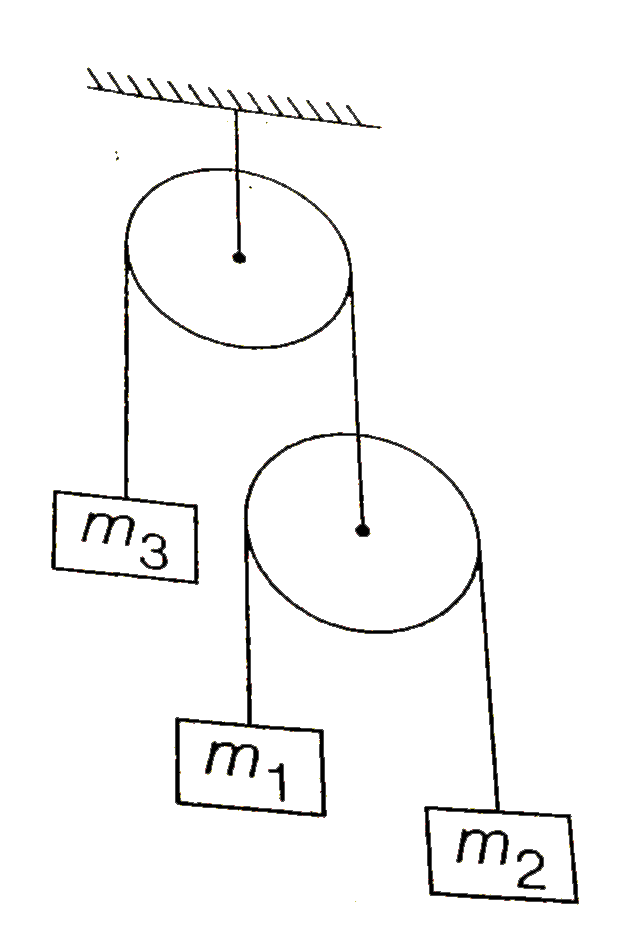 A1 kgB23kgC14kgD2kg
A1 kgB23kgC14kgD2kgThree blocks A,B and C of mass 10 kg each are hanging on a string passing over a fixed frictionless pulley as shown in figure. The tension in the string connecting blocks B and C is (g=10m/s2)
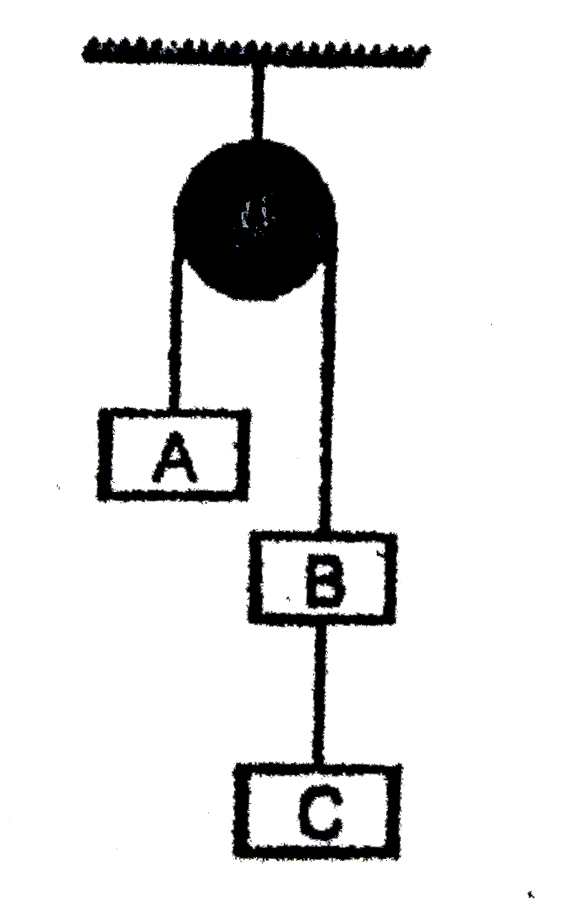 A20003NB4003NC100 ND2003N
A20003NB4003NC100 ND2003N
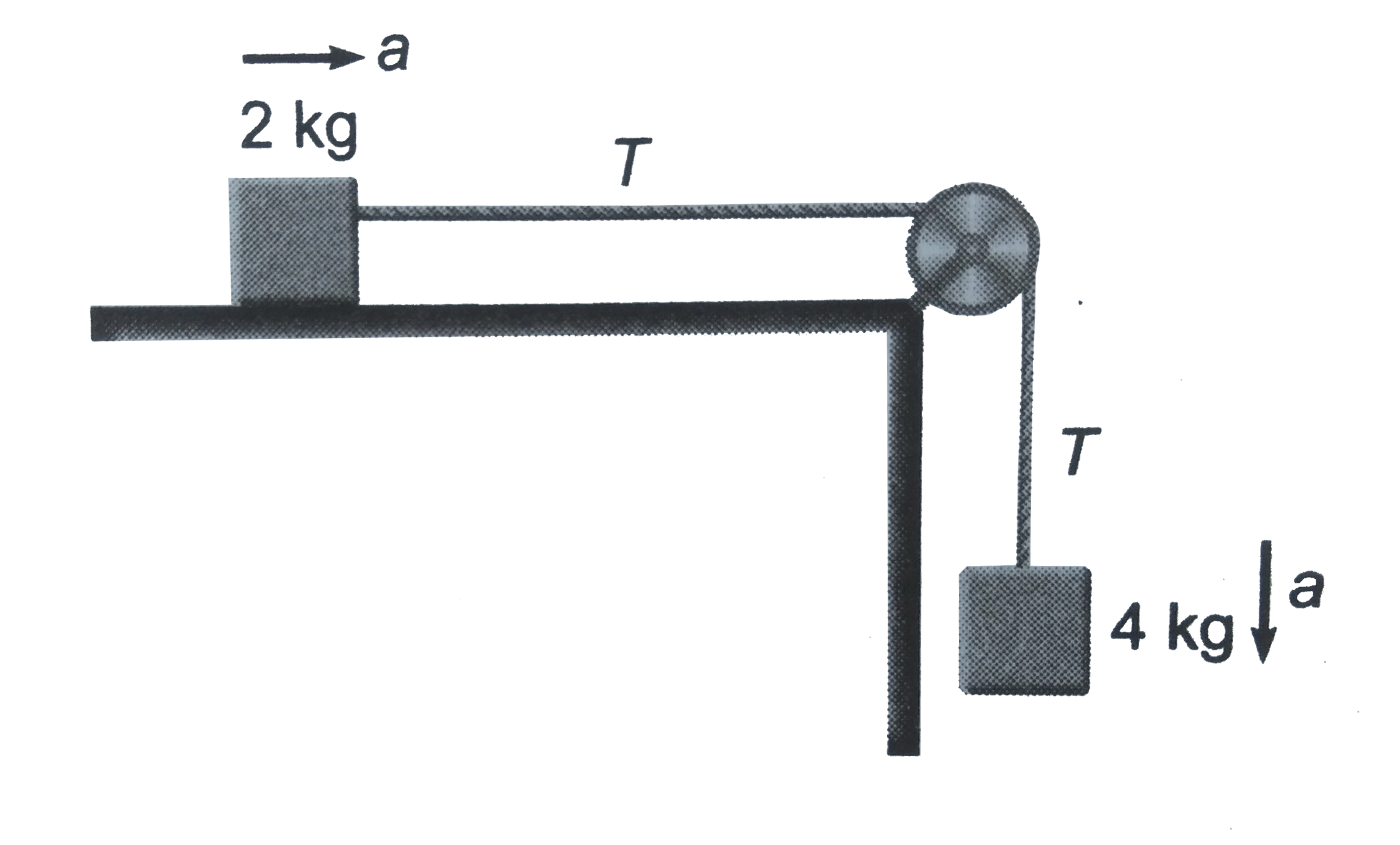
In the system shown in figure all surfaces are smooth. Strings is massless and inextensible.Find acceleration of the system and tension T in the string (g=10m/s2)
View SolutionPulleys shown in the system are massless and fricionless. Threads are inextensible. The mass of blocks A, B, and C are m1=2kg,m2=4kg, and (m3)=2.75kg, respectively. Calculate the acceleration of each block.

View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
Find the tension in the string
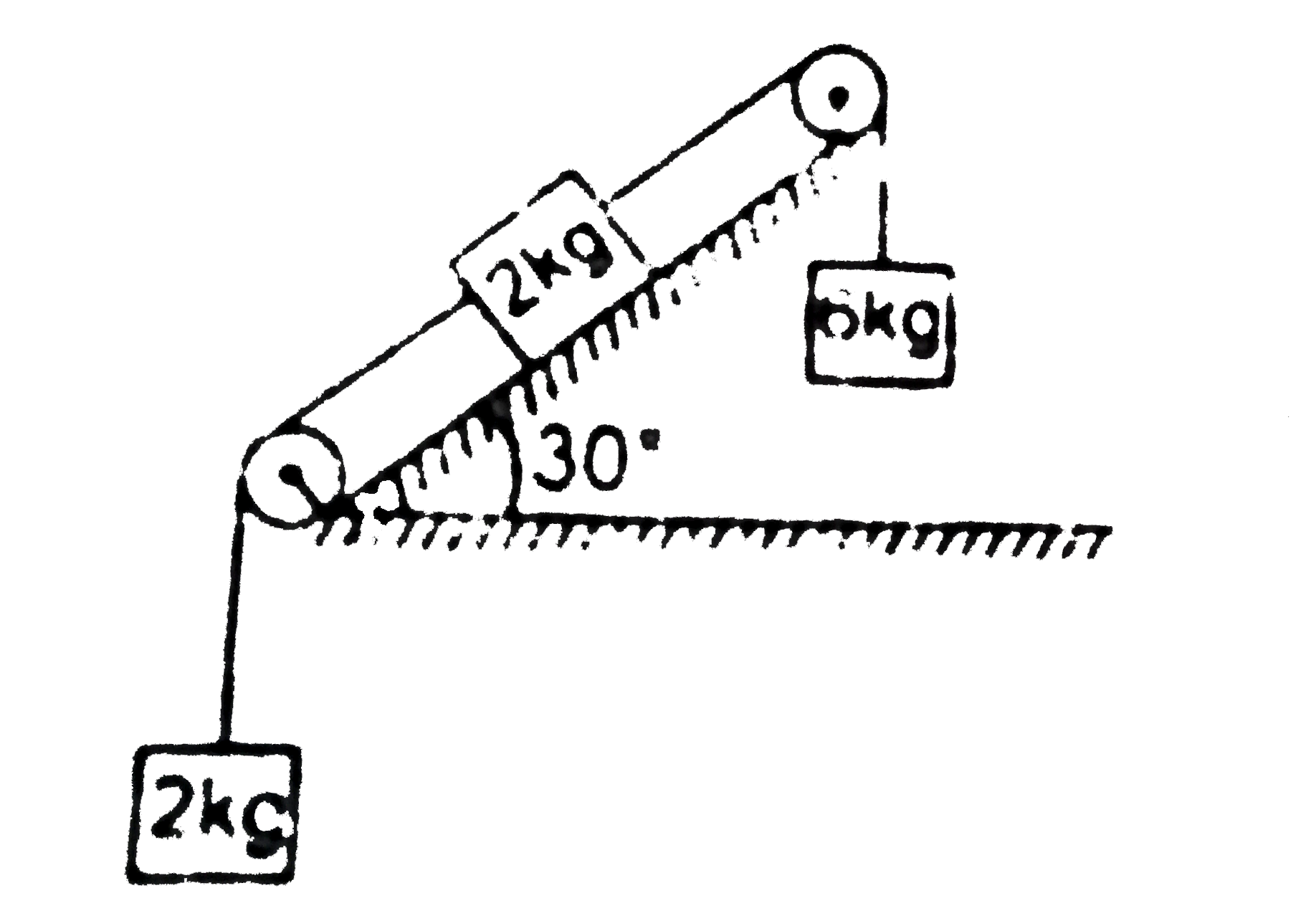
View SolutionFind the acceleration of the 6 kg block in the figure. All the surfaces and pulleys are smooth. Also the strings are inextensible and light. [Take g=10m/s2]
 .
.
View SolutionIn the figure shown tension in string AB always lies between m1g and m2g. (m1≠m2)

Tension in massless string is uniform throughout.
View Solution

