In the figure shown tension in string AB always lies between m1g and m2g. (m1≠m2)

Tension in massless string is uniform throughout.
If both Accertion and Reason are true and the reason is correct explanation of the Assertion.
If both Assertion and Reason are true but reason is not the correct explanation of Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:B
If m1>m2
a=Net pulling forceTotal mass=(m1−m2)gm1+m2
FBD of m1
m1g−T=m1a=m1(m1−m2)gm1+m2
:. T=2m1m2(m1+m2)g
=m1g[2m2m1+m2]=m2g[2m1m1+m2]
=m1g[m2+m2m1+m2]=m2g[m1+m1m1+m2]
Since m1>m2, T<m1g but T>m2g
Similarly, we can prove that
T<m2g
T>m1g
m2>m1
Therefore under all condition T lines between m1g and m2.
Similar Questions
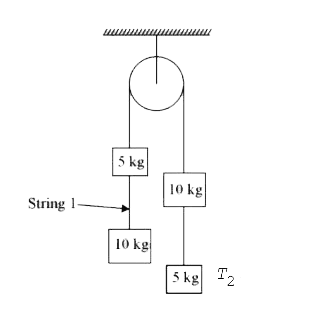
Find the value of tension in string 1 if the system equilibrium ? (g=10 m/s2)
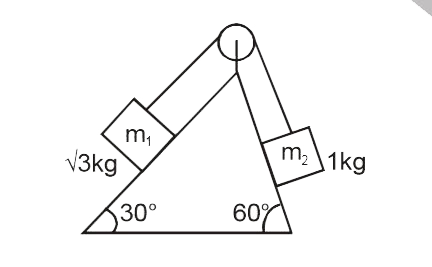
View SolutionTwo blocks m1 and m2 are placed on a smooth inclined plane as shown in figure. If they are released from rest. Find :
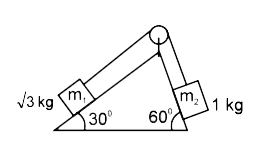
(i) acceleration of mass m1 and m2
(ii) tension in the string
(iii) net force on pulley exerted by string.
View Solution
Knowledge Check
The tension in the string shown in figure m−2m→F is.
AF/3BF/6CF/2D2FIn the situation shown in figure F=500 newton applied on the pulley m1=50kgandm2=10kg and pulley and strings are massless and frictionless. Then the acceleration of the pulley is : [g=10m/s2]
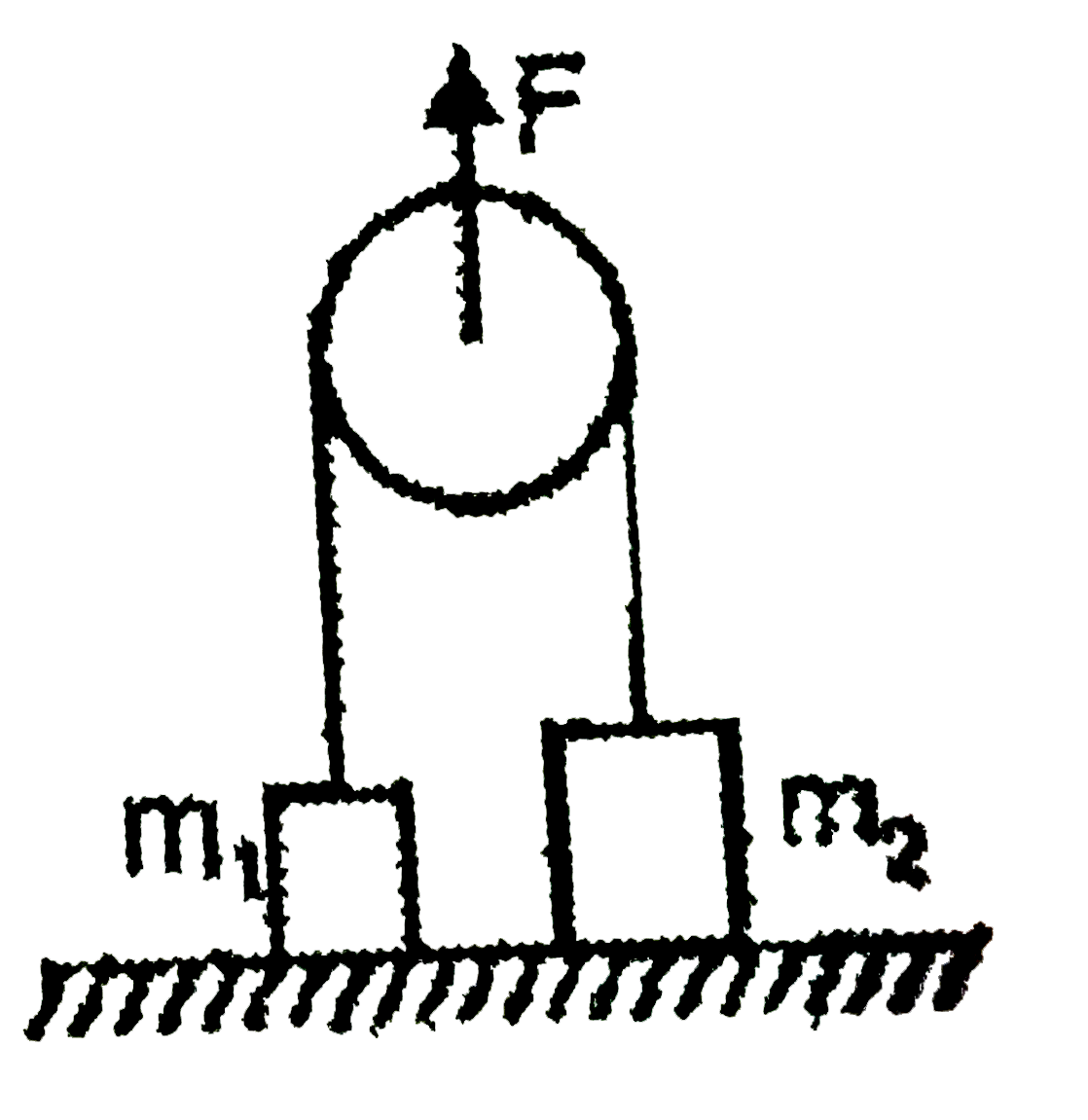 A15m/s2B27.5m/s2C40m/s2D7.5m/s2
A15m/s2B27.5m/s2C40m/s2D7.5m/s2A lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T1. Two masses of m1andm2 are connected with inextensible light string and tension in this string T2 as shown in figure. Read the questionbs carefully and answer
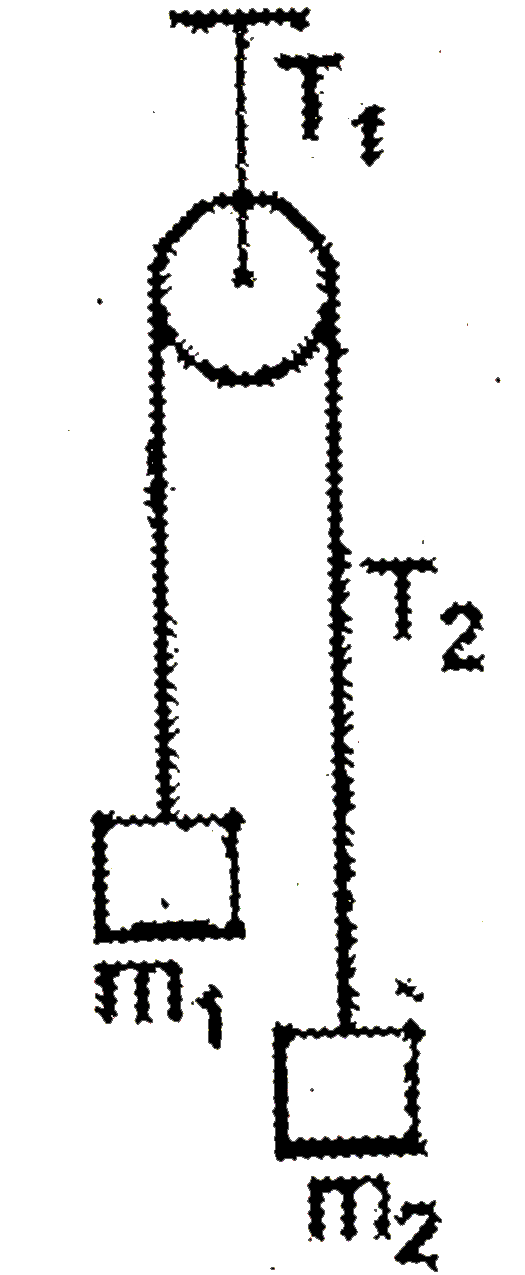
If m1+m2=m and lift is moving with constant velocity then value of T1 :A≥mgB=mgC≤mgD>mg
Two block m1 and m2 are placed on a smooth inclined plane as shown in figure. It they are released from rest.
Find :
(i) acceleration of mass m1 and m2
(ii) tension in the string
(iii) net force on pulley exerted by string
View SolutionA lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T1. Two masses of m1andm2 are connected with inextensible light string and tension in this string T2 as shown in figure. Read the questionbs carefully and answer

If m1 is very small as compared to m2 and lift is moving with constant velocity then value of T2 is nearly :
View SolutionA lift can move upward or downward. A light inextensible string fixed from ceiling of lift when a frictionless pulley and tensions in string T1. Two masses of m1andm2 are connected with inextensible light string and tension in this string T2 as shown in figure. Read the questionbs carefully and answer
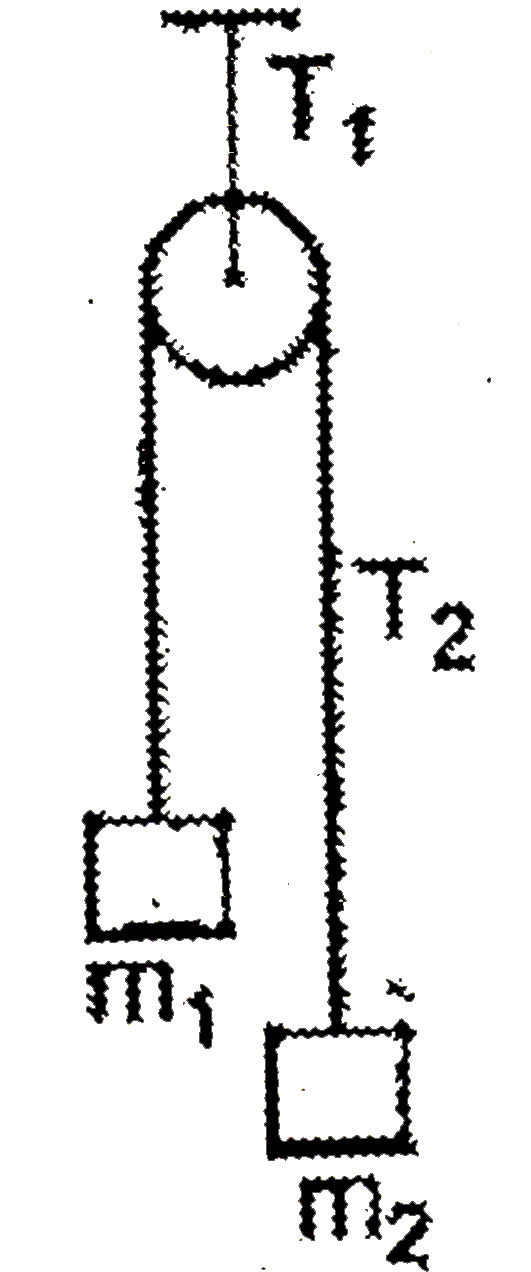
If m1=m2andm1 is moving at a certain instant with velocity v upward with respect to lift and the lift is moving in upward direction with constant acceleration (a<g) then speed of m1 with respect to lift :
View SolutionIn the arrangement shown in the figure the mass M is very heavy compared to m(M>>m). The tension T in the string suspende from the ceiling is

View SolutionIn fig. both pulleys and the string are massless and all the surfaces are frictionless.

Given m1=1kg,m2=2kg,m3=3kg.
Find the tension in the string
View Solution

