Two bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
3m1m2m1+m2g
m1+m24m1m2g
2m1m2m1+m2g
m1m2m1+m2g
The correct Answer is:A
To find the tension in the string connecting two masses m1 and m2 over a frictionless, massless pulley that is accelerating upwards with an acceleration of g2, we can follow these steps:
Step 1: Identify the Forces Acting on Each Mass
1. For mass m1 (which is lighter):
- Weight acting downwards: m1g
- Tension T acting upwards.
- Since the pulley is accelerating upwards, the effective acceleration acting on m1 is g2 upwards.
The net force equation for m1 can be written as:
T−m1g=−m1(g2)
(The negative sign indicates that the acceleration is upwards against the weight.)
2. For mass m2 (which is heavier):
- Weight acting downwards: m2g
- Tension T acting upwards.
- The effective acceleration acting on m2 is also g2 upwards.
The net force equation for m2 can be written as:
m2g−T=m2(g2)
Step 2: Set Up the Equations
From the equations derived from the forces acting on m1 and m2:
1. For m1:
T−m1g=−m1g2(1)
2. For m2:
m2g−T=m2g2(2)
Step 3: Solve the Equations
From equation (1):
T=m1g−m1g2=m1g2(3)
From equation (2):
T=m2g−m2g2=m2g2(4)
Step 4: Equate the Two Expressions for Tension
From equations (3) and (4):
m1g2=m2g−m2g2
Step 5: Simplify and Solve for Tension
Combine and simplify:
m1g2+m2g2=m2g
(m1+m2)g2=m2g
This leads to:
T=m1g+m2g2=(m1+m2)g2
Final Expression for Tension
Thus, the tension T in the string is given by:
T=(m1+m2)g2
1. For mass m1 (which is lighter):
- Weight acting downwards: m1g
- Tension T acting upwards.
- Since the pulley is accelerating upwards, the effective acceleration acting on m1 is g2 upwards.
The net force equation for m1 can be written as:
T−m1g=−m1(g2)
(The negative sign indicates that the acceleration is upwards against the weight.)
- Weight acting downwards: m2g
- Tension T acting upwards.
- The effective acceleration acting on m2 is also g2 upwards.
The net force equation for m2 can be written as:
m2g−T=m2(g2)
From the equations derived from the forces acting on m1 and m2:
T−m1g=−m1g2(1)
m2g−T=m2g2(2)
From equation (1):
T=m1g−m1g2=m1g2(3)
T=m2g−m2g2=m2g2(4)
From equations (3) and (4):
m1g2=m2g−m2g2
Combine and simplify:
m1g2+m2g2=m2g
(m1+m2)g2=m2g
This leads to:
T=m1g+m2g2=(m1+m2)g2
Thus, the tension T in the string is given by:
T=(m1+m2)g2
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.4
20 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Chapter exercises (A) Taking it together
71 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Check point 5.2
15 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
Two blocks of masses m1 and m2 are attached at the ends of an inextensible string which passes over a smooth massless pulley. If m1>m2, find :
(i) the acceleration of each block
(ii) the tension in the string.
View SolutionTwo blocks of masses 2 kg and 4 kg are hanging with the help of massless string passing over an ideal pulley inside an elevator. The elevator is moving upward with an acceleration g2. The tension in the string connected between the blocks will be (Take g=10m/s2).
View Solution
Knowledge Check
Two masses m1 and m2 are connected by light inextensible string passing over a smooth pulley P. If the pulley moves vertically upwards with an acceleration equal to g then
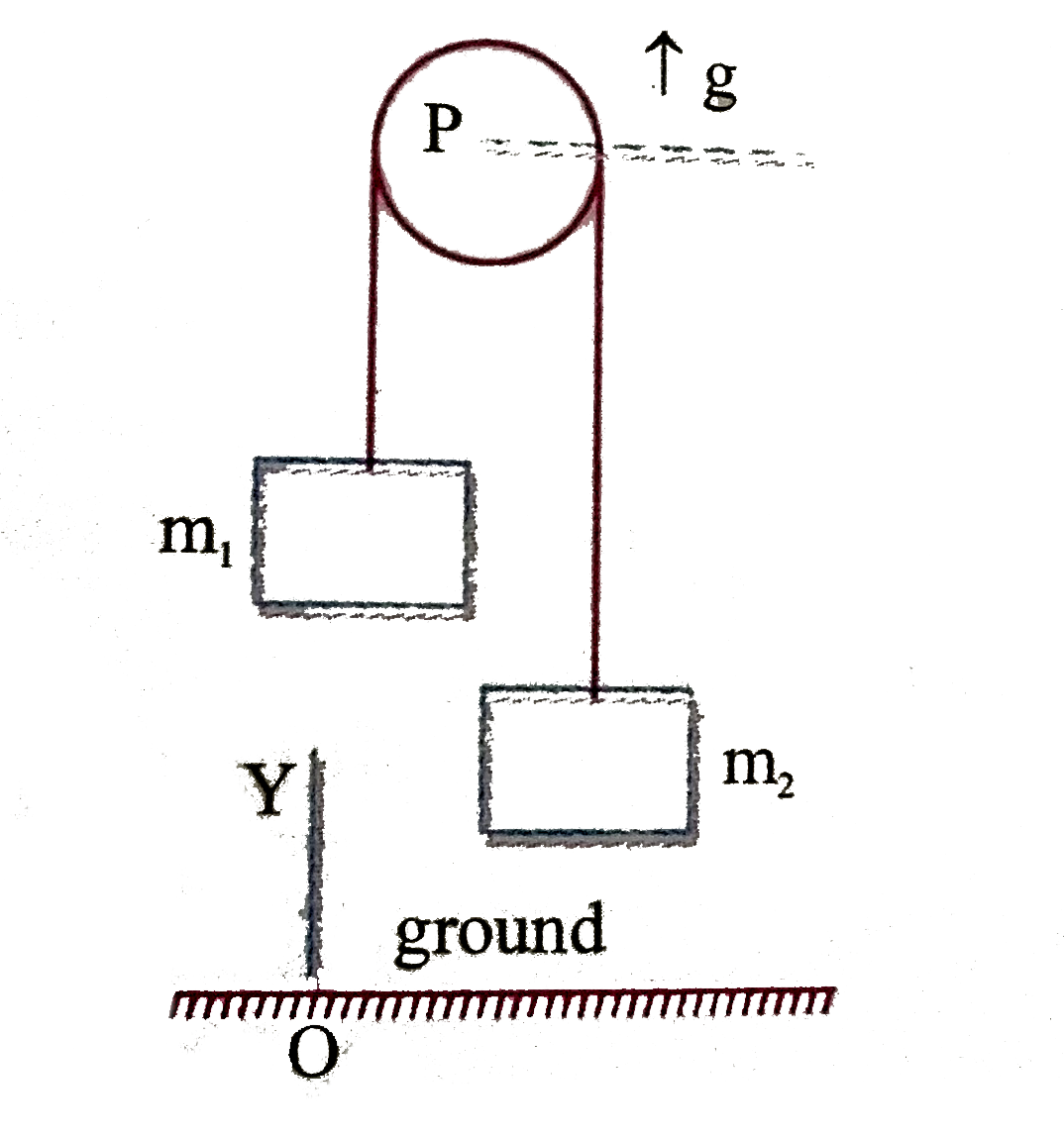 .ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2g
.ATension on the string is 4m1m2gm1+m2BTension on the string is 2m1m2gm1+m2CThe acceleration of mass m1 with respect to ground is 3m2−m1m1+m2g .DThe acceleration of mass m1 with respect to ground is 2(m2−m)m1+m2gTwo weights w1 and w2 are suspended from the ends of a light string passing over a smooth fixed pulley. If the pulley is pulled up at an acceleration g , the tension in the string will be
A4w1w2w1+w2B2w1w2w1+w2Cw1w2w1+w2Dw1w22(w1+w2)Two mass m and 2m are attached with each other by a rope passing over a frictionless and massless pulley. If the pulley is accelerated upwards with an acceleration 'a', what is the value of tension?
Ag+a3Bg−a3C4m(g+a)3Dm(g−a)3
Two masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo masses 2 kg and 4 kg are connected at two ends of light inextensible string passing over a frictionless pulley . If the masses are released , then find the accelaration of the masses and the tension in the string .
View SolutionTwo bodies of masses 2kg and 3kg are connected by a very light string passed over a clamped light smooth pulley. If the system is released from rest, find the acceleration of the two masses and the tension in the string (g=10ms−2)
View SolutionConsider the case of two bodies of masses m1andm2 which are connected by light inextensible string passing over a light smooth pulley as shown in the figure. The expression for acceleration of the system and tension of the string are expressed below under different situations:
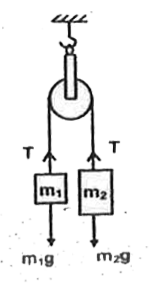
(i) when m1>m2. In this case
a=(m1−m2m1+m2)gandT=(2m1m2m1+m2)g
(ii) when m2>m1. In this case
a=(m2−m1m1+m2)gandT=(2m1m2m1+m2)g
(iii) When m1=m2=m. In this case a=0,T=mg
If the pulley is pulled upward with acceleration equal to the acceleration due to gravity, what will be the tension in the string?
View SolutionTwo masses m1 and m2 are attached to a string which passes over a frictionless smooth pulley. When m1=10kg,m2=6kg, the acceleration of masses is
View Solution
