Two blocks of masses 2 kg and 4 kg are hanging with the help of massless string passing over an ideal pulley inside an elevator. The elevator is moving upward with an acceleration g2. The tension in the string connected between the blocks will be (Take g=10m/s2).
40 N
60 N
80 N
20 N
To solve the problem of finding the tension in the string connecting two blocks of masses 2 kg and 4 kg hanging in an elevator that is accelerating upward with an acceleration of g2, we will follow these steps:
Step 1: Identify the Forces Acting on Each Block
1. For the 4 kg block (let's call it M2):
- Weight W2=M2⋅g=4⋅10=40N (downward)
- Pseudo force due to the upward acceleration of the elevator Fp2=M2⋅a=4⋅g2=4⋅5=20N (downward)
- Tension T (upward)
2. For the 2 kg block (let's call it M1):
- Weight W1=M1⋅g=2⋅10=20N (downward)
- Pseudo force due to the upward acceleration of the elevator Fp1=M1⋅a=2⋅g2=2⋅5=10N (downward)
- Tension T (upward)
Step 2: Write the Equations of Motion
1. For the 4 kg block:
T+Fp2=W2+a⋅M2
Which gives:
T+20=40+4a(1)
2. For the 2 kg block:
T−Fp1=W1−a⋅M1
Which gives:
T−10=20−2a(2)
Step 3: Solve the Equations
1. From equation (1):
T=40+4a−20
Simplifying gives:
T=20+4a(3)
2. From equation (2):
T=20−2a+10
Simplifying gives:
T=30−2a(4)
Step 4: Equate the Two Expressions for Tension
Set equations (3) and (4) equal to each other:
20+4a=30−2a
Solving for a:
4a+2a=30−20
6a=10⟹a=106=53m/s2
Step 5: Substitute a Back to Find Tension
Substituting a back into equation (3):
T=20+4(53)
Calculating gives:
T=20+203=603+203=803≈26.67N
Final Answer
The tension in the string is approximately 26.67N.
1. For the 4 kg block (let's call it M2):
- Weight W2=M2⋅g=4⋅10=40N (downward)
- Pseudo force due to the upward acceleration of the elevator Fp2=M2⋅a=4⋅g2=4⋅5=20N (downward)
- Tension T (upward)
- Weight W1=M1⋅g=2⋅10=20N (downward)
- Pseudo force due to the upward acceleration of the elevator Fp1=M1⋅a=2⋅g2=2⋅5=10N (downward)
- Tension T (upward)
1. For the 4 kg block:
T+Fp2=W2+a⋅M2
Which gives:
T+20=40+4a(1)
T−Fp1=W1−a⋅M1
Which gives:
T−10=20−2a(2)
1. From equation (1):
T=40+4a−20
Simplifying gives:
T=20+4a(3)
T=20−2a+10
Simplifying gives:
T=30−2a(4)
Set equations (3) and (4) equal to each other:
20+4a=30−2a
Solving for a:
4a+2a=30−20
6a=10⟹a=106=53m/s2
Substituting a back into equation (3):
T=20+4(53)
Calculating gives:
T=20+203=603+203=803≈26.67N
The tension in the string is approximately 26.67N.
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH INSTITUTEChapter:LAWS OF MOTIONExercise:Assignment (SECTION-A)
Explore 65 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTEChapter:LAWS OF MOTIONExercise:Assignment (SECTION-B)
Explore 44 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTEChapter:LAWS OF MOTIONExercise:Example
Explore 24 Videos
- KINETIC THEORYBook:AAKASH INSTITUTEChapter:KINETIC THEORYExercise:EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
Explore 10 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTEChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
Similar Questions
Two masses 2 kg and 4 kg are connected at the two ends of light inextensible string passing over a frictionless pulley. If the masses are released, then find the acceleration of the masses and the tension in the string.
View SolutionTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View Solution
Knowledge Check
If the elevator in shown figure is moving upwards with constant acceleration 1ms−2, tension in the string connected to block A of mass 6 kg would be ( take, g=10ms−2)
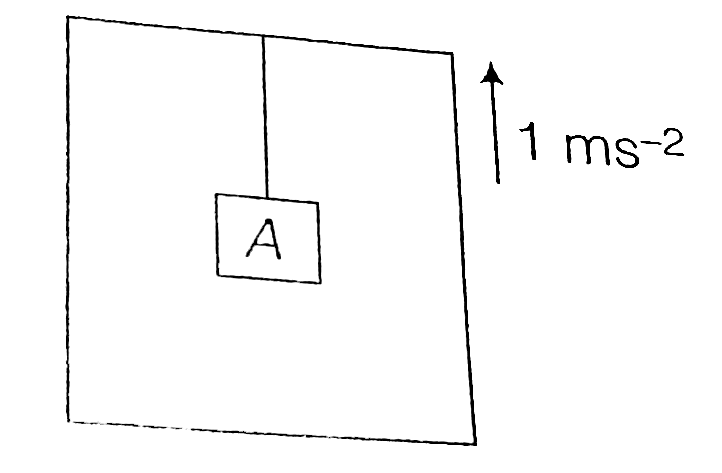 A60 NB66 NC54 ND42 N
A60 NB66 NC54 ND42 NTwo bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
A3m1m2m1+m2gBm1+m24m1m2gC2m1m2m1+m2gDm1m2m1+m2gTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two bodies of mass 3 kg and 4 kg are suspended at the ends of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
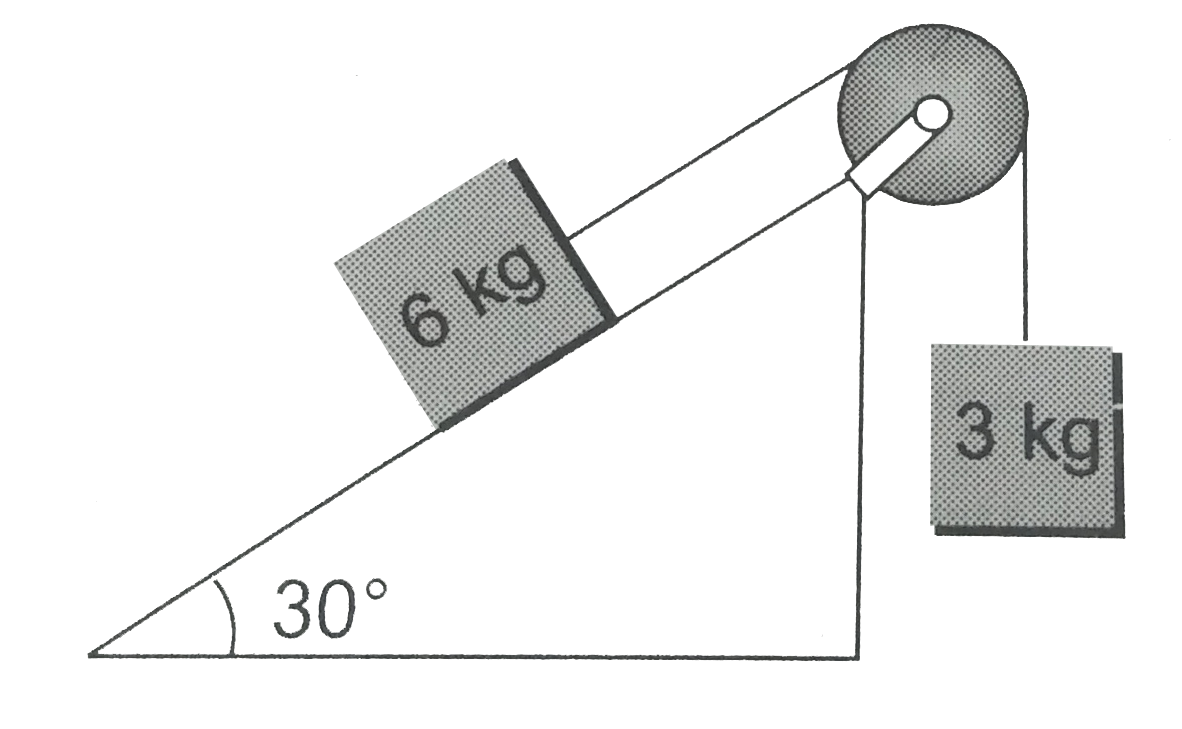
View SolutionTwo bodies of mass 3kg and 4kg are suspended at the ends of massless string passing over a frictionless pulley. The acceleration of the system is (g=9.8m/s2)
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View Solution

