A block of mass m kg is kept on a weighing machine in an elevator. If the elevator is retarding upward by a ms−2, the reading of weighing machine is (in kgf)
mg
m(g−a)
m(1−1g)
m(g+a)
To solve the problem, we need to determine the reading of the weighing machine when a block of mass m kg is placed on it inside an elevator that is retarding upward with an acceleration of a m/s².
1. Understanding the Forces:
- The block has a weight acting downwards, which is given by W=mg, where g is the acceleration due to gravity (approximately 9.81m/s2).
- The elevator is retarding upward, which means it is decelerating as it moves upwards. Therefore, the effective acceleration acting on the block is downward.
2. Identifying the Effective Acceleration:
- Since the elevator is retarding upward with an acceleration a, the effective acceleration acting on the block is g−a (because the upward direction is considered positive).
- Thus, the net downward acceleration acting on the block is g−a.
3. Applying Newton's Second Law:
- According to Newton's second law, the net force acting on the block is equal to the mass of the block multiplied by its acceleration.
- The forces acting on the block are the normal force N (upward) and the weight mg (downward). Therefore, we can write:
N−mg=−m(g−a)
- Rearranging this gives:
N=mg−m(g−a)
4. Simplifying the Equation:
- Simplifying the expression for N:
N=mg−mg+ma
N=ma
5. Final Reading of the Weighing Machine:
- The reading of the weighing machine is equal to the normal force N. Therefore, the reading in kgf (kilogram-force) is:
N=m(g−a)
- To express this in kgf, we can divide by g (since 1kgf=9.81N):
Reading in kgf=Ng=m(g−a)g
Conclusion:
The reading of the weighing machine in kgf is given by:
Reading=m(1−ag)
- The block has a weight acting downwards, which is given by W=mg, where g is the acceleration due to gravity (approximately 9.81m/s2).
- The elevator is retarding upward, which means it is decelerating as it moves upwards. Therefore, the effective acceleration acting on the block is downward.
- Since the elevator is retarding upward with an acceleration a, the effective acceleration acting on the block is g−a (because the upward direction is considered positive).
- Thus, the net downward acceleration acting on the block is g−a.
- According to Newton's second law, the net force acting on the block is equal to the mass of the block multiplied by its acceleration.
- The forces acting on the block are the normal force N (upward) and the weight mg (downward). Therefore, we can write:
N−mg=−m(g−a)
- Rearranging this gives:
N=mg−m(g−a)
- Simplifying the expression for N:
N=mg−mg+ma
N=ma
- The reading of the weighing machine is equal to the normal force N. Therefore, the reading in kgf (kilogram-force) is:
N=m(g−a)
- To express this in kgf, we can divide by g (since 1kgf=9.81N):
Reading in kgf=Ng=m(g−a)g
The reading of the weighing machine in kgf is given by:
Reading=m(1−ag)
Topper's Solved these Questions
- LAWS OF MOTIONBook:AAKASH INSTITUTEChapter:LAWS OF MOTIONExercise:Assignment (SECTION-A)
Explore 65 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTEChapter:LAWS OF MOTIONExercise:Assignment (SECTION-B)
Explore 44 Videos
- LAWS OF MOTIONBook:AAKASH INSTITUTEChapter:LAWS OF MOTIONExercise:Example
Explore 24 Videos
- KINETIC THEORYBook:AAKASH INSTITUTEChapter:KINETIC THEORYExercise:EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
Explore 10 Videos
- MAGNETISM AND MATTER Book:AAKASH INSTITUTEChapter:MAGNETISM AND MATTER Exercise:ASSIGNMENT (SECTION D)
Explore 26 Videos
Similar Questions
A man of mass 75kg stands on a weighing machine in a lift which is moving upwards with uniform acceleration 1.2ms−2,find the reading of weighing machine.
View SolutionA 80 kg man is standing on a weightless weighing machine as shown in the figure if mass of hanging block is 40 kg, then reading of weighing machine, is
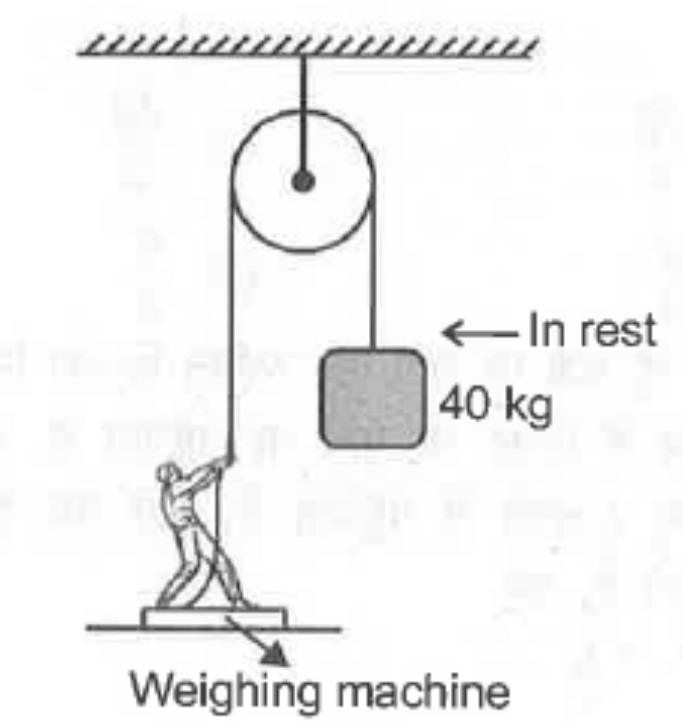
View Solution
Knowledge Check
An elevator is accelerating upwards with an acceleration of 6m/s2 inside it a person of mass 50 kg is standing on a weighing machine which is kept on an inclined plane having angle of inclination 60∘ The reading of the weighing machine is:
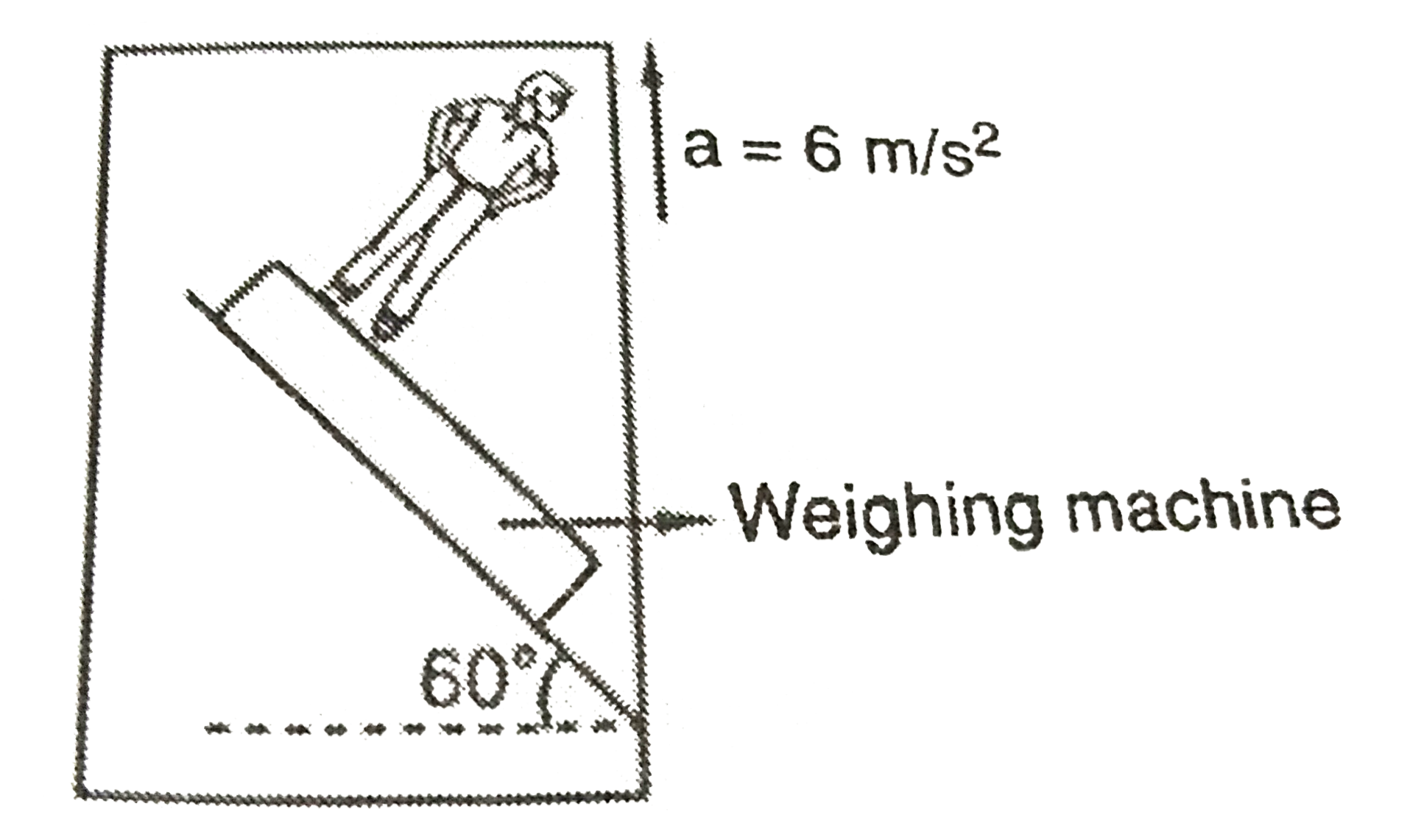 A40 kgB160 kgC80 kgD50 kg
A40 kgB160 kgC80 kgD50 kgAn elevator is accelerating upwards with an acceleration of 6m/s2 . Inside it a person of mass 50kg is standing on a weighing machine which is kept on an inclined plane having angle of inclination 60∘ . The reading of the weighing machine is:
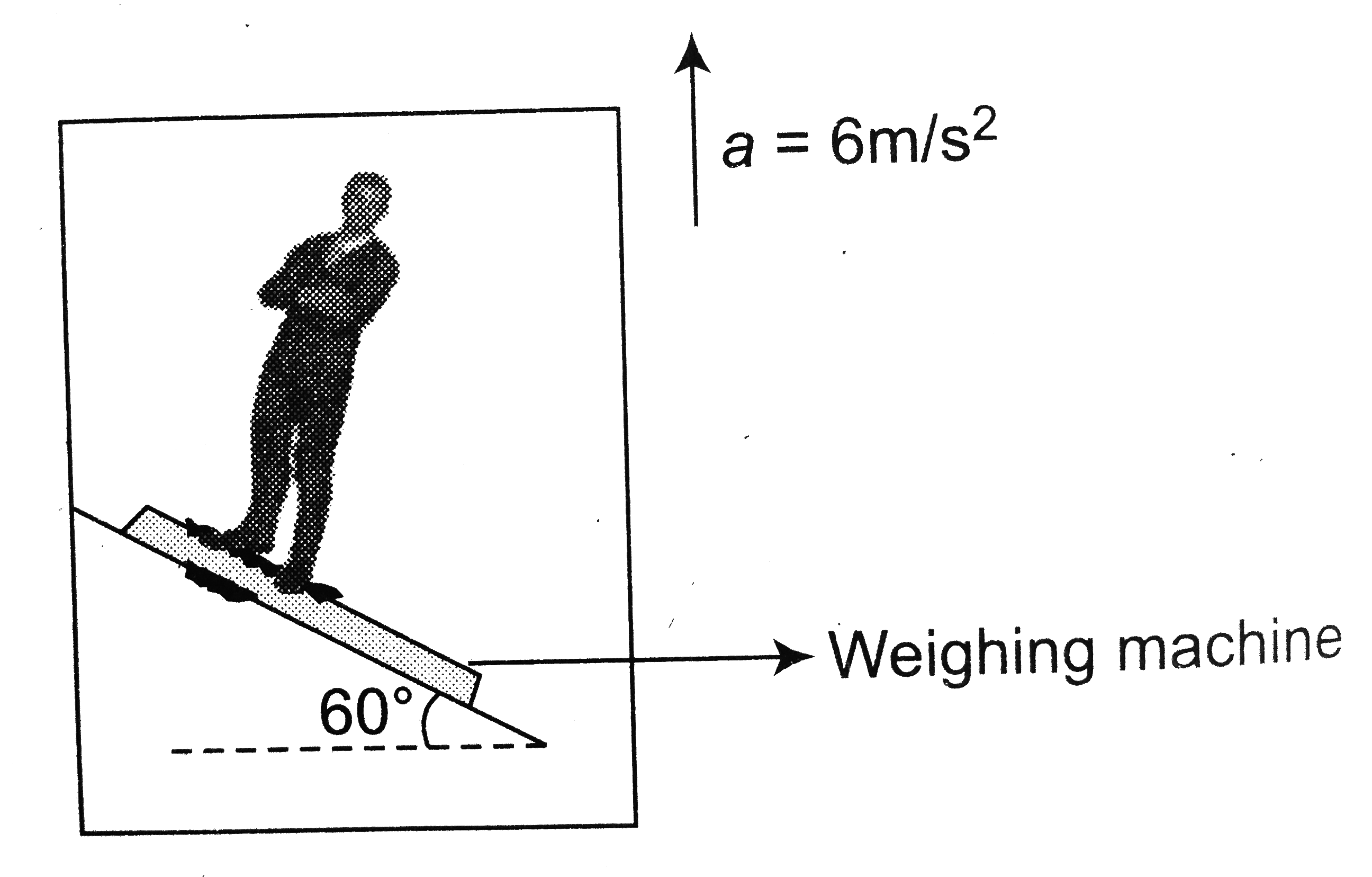 A40kgB160kgC80kgD50kg
A40kgB160kgC80kgD50kgA boy of mass 50kg is standing on a weihing machine placed on the floor of a lift. The machine reads his weight in newtons. The reading of the machine if the lift is moving upwards with uniform speed of 10ms−1 .
A510NB480NC490ND500N
Find out the reading of the weighing machine in the following cases.
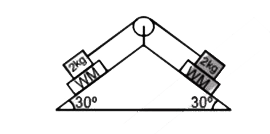
View SolutionA person of mass 50 kg stands on a weighing scale on a lift . If the lift is descending with a downward acceleration of 9ms−2 what would be the reading of the weighing scale? (g=10ms−2) .
View SolutionA body of 100 kg stands on a spring weighing machine inside a lift. The lift starts to ascend with acceleration of 2.2ms−2. What is the reading of the machine inside a lift. The lift starts to ascend with acceleration of 2.2ms−2. What is the reading of the machine?
View SolutionA man of mass M stands on a weighing machine in an elevator accelerating upwards with an acceleration a. Draw the free-body diagram of the man as observed by the observer A (stationary on the ground) and observer B (stationary on the elevator). Also, calculate the reading of the weighing machine.

View SolutionA person stands on a weighing machine kept on the floor of an elevator .When the elevator is at rest then the apparent weight of the person is
View Solution

