Two blocks A and B having masses m1=1kgm2=4kg are arranged as shown in the figure The pulleys P and Q are light and frictionless. All the blocks are resting on a horizontal floor and the pulleys are held such that strings remains just taut. At moment t=0 a force F=30 t (N) starts acting on the pulley P along vertically upward direction as shown in the figure The time when the blocks A and B loose contact with ground is 4/x sec then x is:
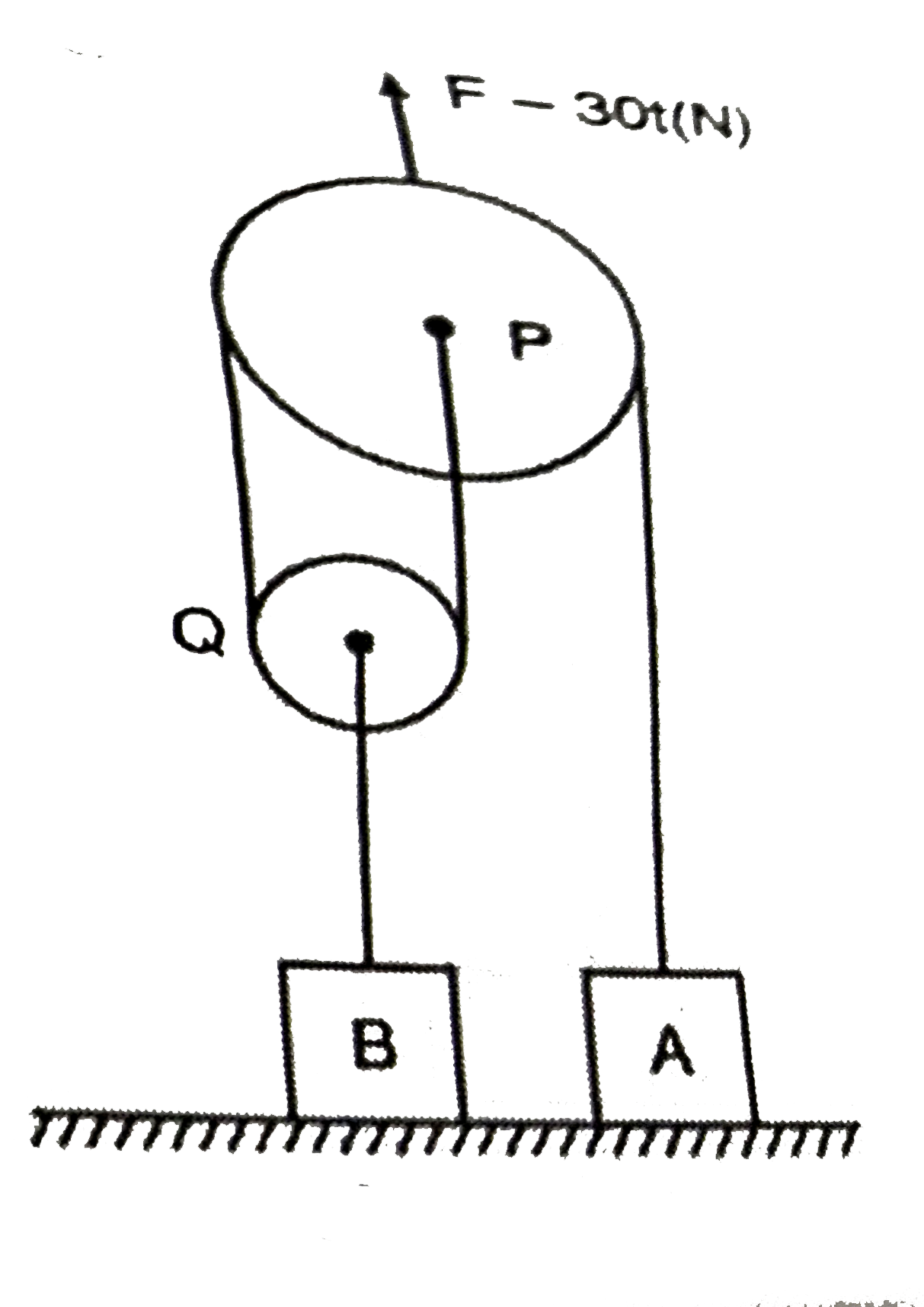
The correct Answer is:2
When blocks loose contact with ground normal reaction on them becomeszero.
(i) When A looses contact T=10N,F=3t
or 30t=30,t=1sec When B looses contact
2T=40 or T=20,F=3T or 30t=60 or t=2sec
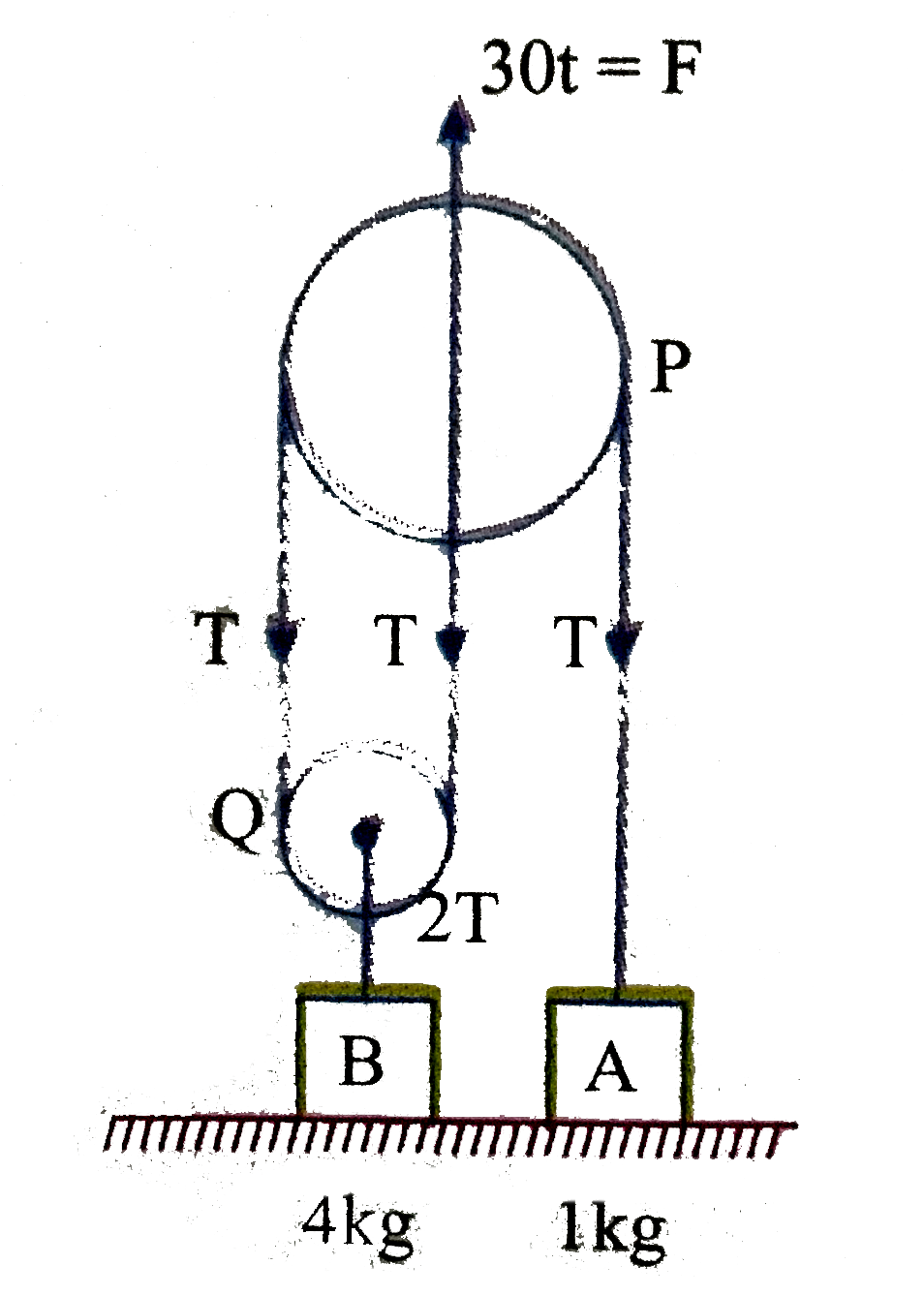 .
.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:MULTIPLE ANSWER QUESTIONS
Explore 9 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:SINGLE ANSWER QUESTIONS Passage -1
Explore 1 Video
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - IV
Explore 41 Videos
Similar Questions
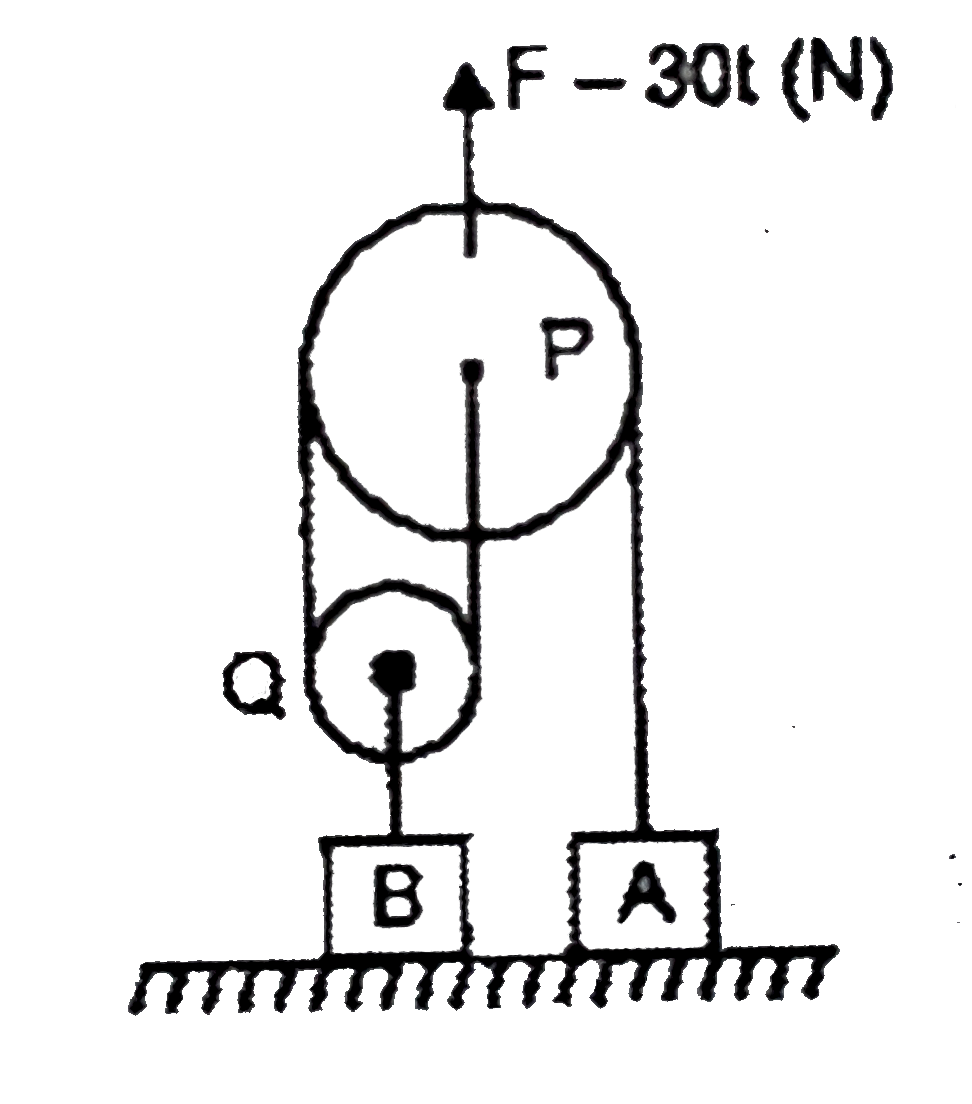
Two block a and B having masses m1=1kg,m2=4kg are arranged as shown in the figure. The pulleys P and Q are light, and frictionless. All the blocks are resting on. a horizontal floor and the pulleys ate held such that strings remains just taut.
At.moment t=0a force F=30t(N) starts acting on thei ipulley p along . vertically upward direction as shown in the pulley P along vertically upward direction as shown in the figure. Calculate.
(i) the time when the blocks A and B loose contact with ground.
(ii) the. velocity of A when B looses contact with ground.
(iii) the height raised. by A upto this instant.
(iv) the work done by the force F upto this instan.
View SolutionTwo block A and B of masses 1kg and2kg respectively are connected by a string, passing over a light frictionless pulley B as shown. Another string connect the center of pulley. Both the blocks are resting on a horizontal floor and the pulley is help such that string remains just taut. At moment t=0, a force F=20t starts acting on the pully along vertically upwards direction as shown in figure.Calculate

(a) velicity of A when B loses contact with the floor.
(b) height raised by the pulley upto that instant.
(Take =g=10m/s2)
View Solution
Knowledge Check
Two blocks, each having a mass M, rest on frictionless surfaces as shown in the figure. If the pulleys are light and frictionless and M on the incline is allowed to move down, then the tension in string will be
 A23MgsinθB32MgsinθCMgsinθ2D2Mgsinθ
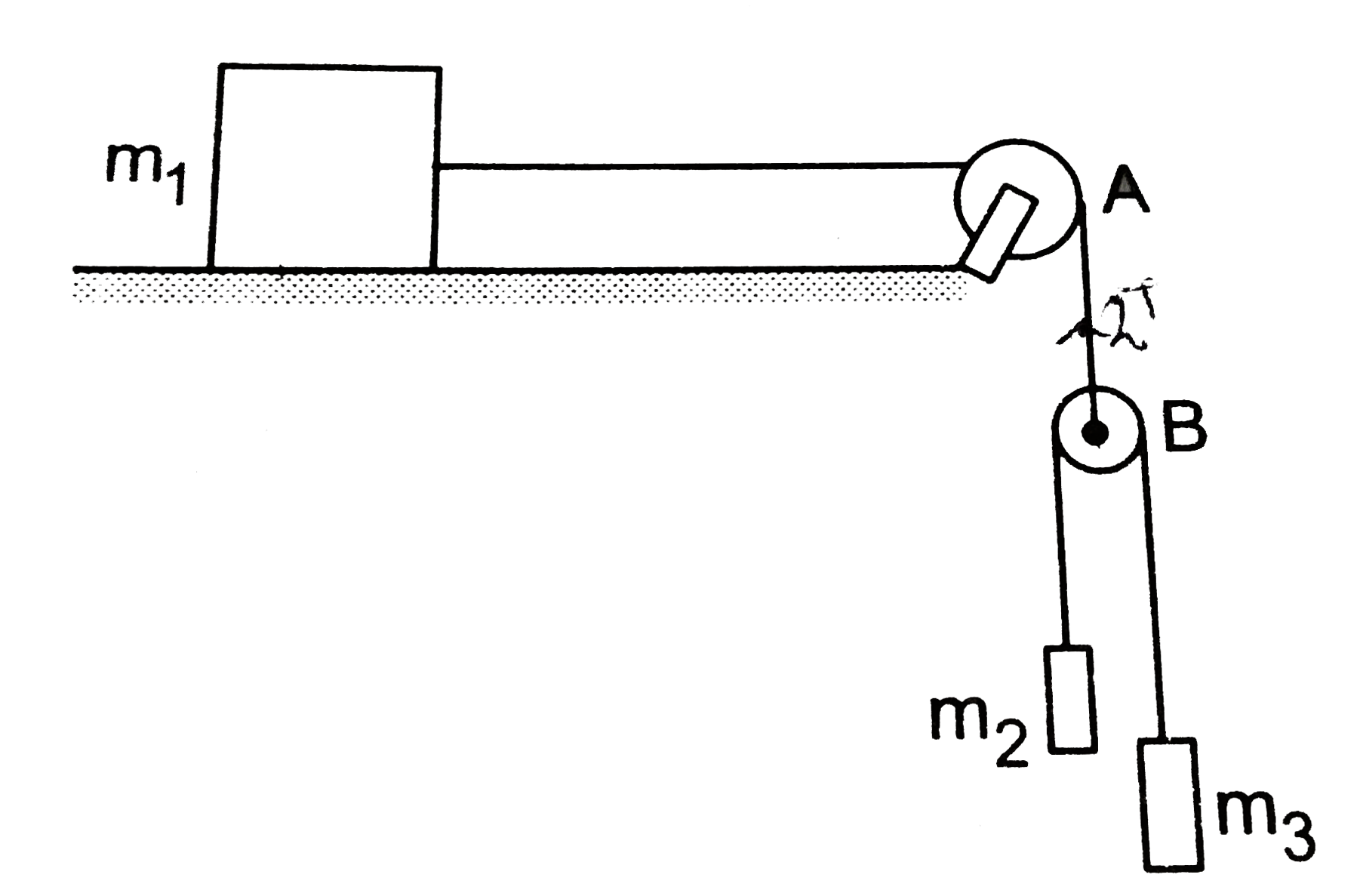
A23MgsinθB32MgsinθCMgsinθ2D2MgsinθIn the arrangement shown below, pulleys are mass-less and friction-less and threads are in-extensible. Block of mass m1 will remain at rest if :
 A4m1=1m2+1m3Bm1=m2=m3C1m1=1m2+1m3D1m2=2m2+3m1
A4m1=1m2+1m3Bm1=m2=m3C1m1=1m2+1m3D1m2=2m2+3m1Two blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is
 A4m/s2B2m/s2CzeroD6m/s2
A4m/s2B2m/s2CzeroD6m/s2
In the arrangement shown in figure, mA=1kg and mB=2kg, while all the pulleys and strings are massless and frictionless. At t=0, a force F=10t starts acting over central pulley in vertically upward direction. If the velocity of A is x×10m/s when B loses contact with floor, find x.
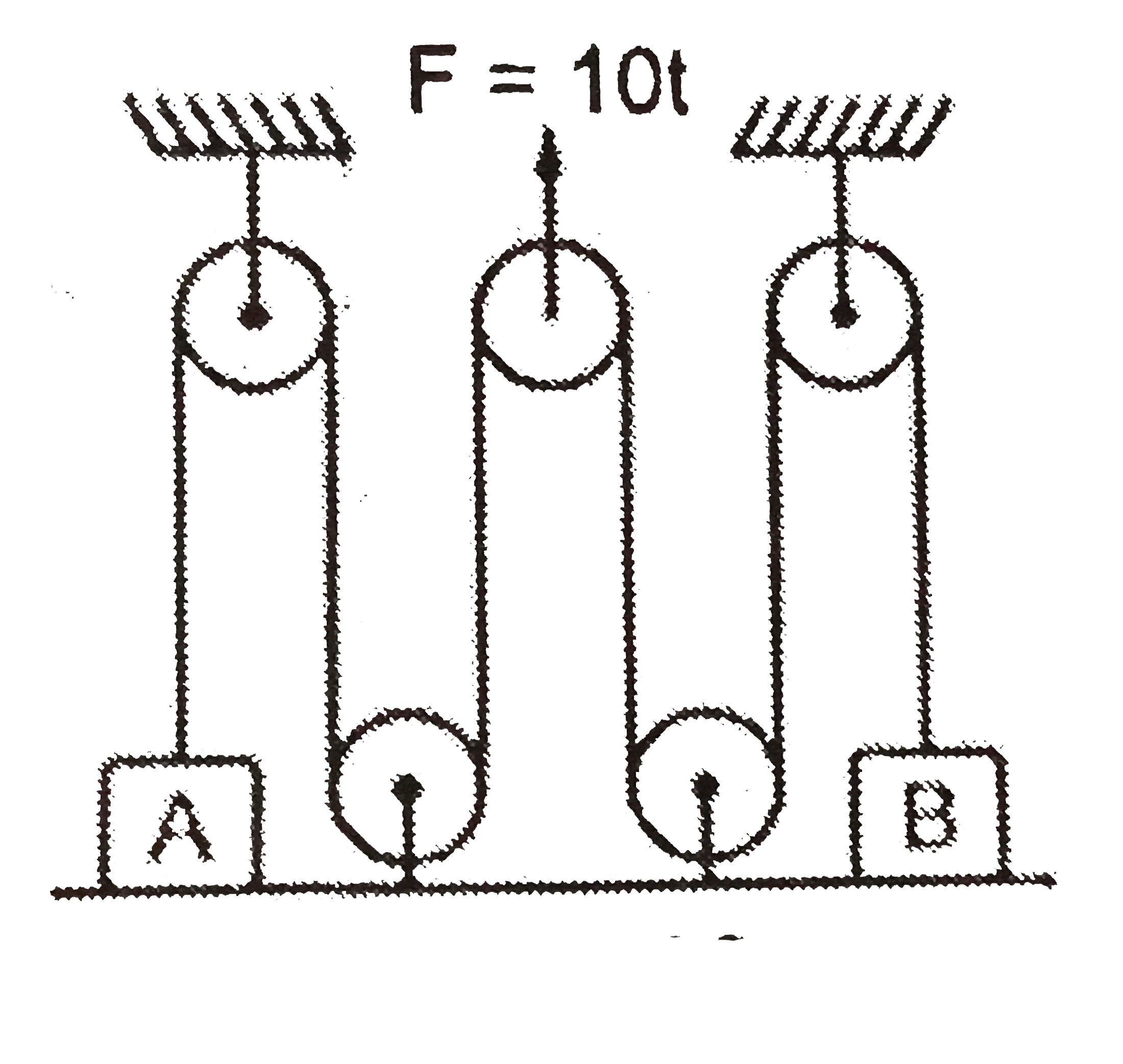
View SolutionTwo blocks A and B are arranged as shown in figure.The pulleys are light and frictionless.The strings are light and inextensible.If the acceleration of the block B is 3ms2 ,then the acceleration of the block A is __________ms2
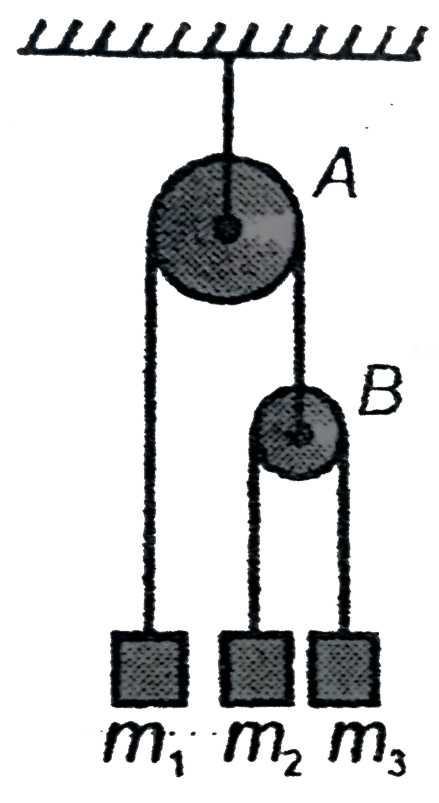
View SolutionThree blocks of masses m1,m2andm3 are connected as shown in the figure. All the surfaces are frictionless and the string and the pulleys are light. Find the acceleration of m1
View SolutionIn the arrangement , shown below pulleys are massless and frictionless and threads are inextensible , block of mass m1 will remain at rest if
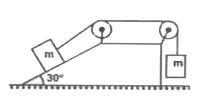
View SolutionTwo blocks, each having mass m, are connected with an ideal string through ideal pulleys on a frictionless fixed wedge as shown in the figure. The acceleration of the blocks is
View Solution

