A man sits on a chair supported by a rope passing over a frictionless fixed pulley. The man who weighs exerts a force of on the chair downwards while pulling the rope on the other side. If the chair weighs then the acceleration of the chair is .
The correct Answer is:C
To solve the problem, we need to analyze the forces acting on the system consisting of the man and the chair.
Step 1: Identify the Forces
1. The weight of the man (W_m) = 1000 N (downward).
2. The force exerted by the man on the chair (F_m) = 450 N (downward).
3. The weight of the chair (W_c) = 250 N (downward).
4. The tension in the rope (T) acts upward on the chair.
Step 2: Write the Net Force Equation
The net force acting on the chair can be expressed as:
Fnet=T−(Wc+Fm)
Where:
- Wc+Fm is the total downward force acting on the chair.
Step 3: Calculate the Total Downward Force
Calculate the total downward force on the chair:
Wc+Fm=250N+450N=700N
Step 4: Apply Newton's Second Law
According to Newton's second law, the net force is also equal to the mass of the chair multiplied by its acceleration (a):
Fnet=mc⋅a
Where mc is the mass of the chair. The weight of the chair is given by:
Wc=mc⋅g
Where g is the acceleration due to gravity (approximately 9.81m/s2). Thus, we can find the mass of the chair:
mc=Wcg=250N9.81m/s2≈25.5kg
Step 5: Substitute and Solve for Acceleration
Now, we can substitute the values into the net force equation:
T−700N=mc⋅a
To find the tension (T), we need to consider the forces acting on the man. The man is pulling the rope with a force of 450 N, which means the tension in the rope is:
T=450N
Now substitute T into the net force equation:
450N−700N=25.5kg⋅a
−250N=25.5kg⋅a
Now, solve for acceleration (a):
a=−250N25.5kg≈−9.8m/s2
Step 6: Interpret the Result
The negative sign indicates that the chair is accelerating downward.
Final Answer
The acceleration of the chair is approximately 9.8m/s2 downward.
---
1. The weight of the man (W_m) = 1000 N (downward).
2. The force exerted by the man on the chair (F_m) = 450 N (downward).
3. The weight of the chair (W_c) = 250 N (downward).
4. The tension in the rope (T) acts upward on the chair.
The net force acting on the chair can be expressed as:
Fnet=T−(Wc+Fm)
Where:
- Wc+Fm is the total downward force acting on the chair.
Calculate the total downward force on the chair:
Wc+Fm=250N+450N=700N
According to Newton's second law, the net force is also equal to the mass of the chair multiplied by its acceleration (a):
Fnet=mc⋅a
Where mc is the mass of the chair. The weight of the chair is given by:
Wc=mc⋅g
Where g is the acceleration due to gravity (approximately 9.81m/s2). Thus, we can find the mass of the chair:
mc=Wcg=250N9.81m/s2≈25.5kg
Now, we can substitute the values into the net force equation:
T−700N=mc⋅a
To find the tension (T), we need to consider the forces acting on the man. The man is pulling the rope with a force of 450 N, which means the tension in the rope is:
T=450N
450N−700N=25.5kg⋅a
−250N=25.5kg⋅a
Now, solve for acceleration (a):
a=−250N25.5kg≈−9.8m/s2
The negative sign indicates that the chair is accelerating downward.
The acceleration of the chair is approximately 9.8m/s2 downward.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -III
Explore 31 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:NCERT BASED QUESTION
Explore 33 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -I (C.W)
Explore 47 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - IV
Explore 41 Videos
Similar Questions
A man sits in a chair that is suspended from arope. The rope passes over a pulley suspended from the ceiling, and the man holds the other end of the rope in his hands.What is the tension in the rope, and what force does the chair exert on the man ?
View SolutionA 60kg painter on a 15 kg platform. A rope attached to the platform and passing over an overhead pulley allows the painter to raise himself along with the platform.
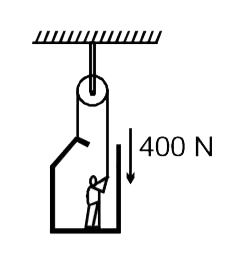
To get started, he pulls the rope down with aforce of 400N. Find the acceleration of the platform as well as that of the painter.
View Solution
Knowledge Check
A man sits on a chair supported by a rope passing over a frictionless fixed pulley. The man who weighs 1,000 N exerts a force of 450 N on the chair downwards while pulling the rope on the other side. If the chair weighs 250N, then the acceleration of the chair is
A0.45m/s2B0C2m/s2D9/25m/s2As shown in the given figure, two blocks are connected by a rope that passes over a set of pulleys. One block has a weight of 412 N, and the other has a weight of 908 N. The rope and the pulleys are massless and there is no friction. What is the acceleration of the lighter block ?
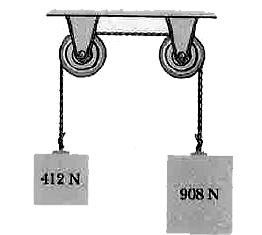 A4.44 m/s2B6.34 m/s2C2.66 m/s2D3.68 m/s2
A4.44 m/s2B6.34 m/s2C2.66 m/s2D3.68 m/s2A rope of length 4 m having mass 1.5 kg/m lying on a horizontal frictionless surface is pulled at one end by a force of 12N. What is the tension in the rope at a point 1.6 m from the other end?
A5NB4.8NC7.2ND6N
A chair weighing 60 N is lifted to a height of 0.8 m and then carried 6 m across the room. How much work is done on the chair?
View SolutionFigure represents a painter in a crate which hangs alongside a building. When the painter of mass 100kg pulls the rope, the force exerted by him on the floor of the crate is 450N. If the crate weighs 25 kg. find the acceleration (in ms−2) of the painter.

View SolutionTwo masses of 5 kg and 10 kg are suspended from a fixed support as shown in the figure. The system is pulled downwards with a force of 150 N applied to the lower mass. The string attached to the support breaks and the system accelerates downwards. If the downward force continues to act, the acceleration of the center of mass of the system is :
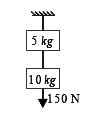
View SolutionA child weighing 25 kg slides down a rope hanging from the branch of a tall tree. If the force of friction acting against him is 2 N , what is the acceleration of the child
View SolutionA block of mass 2.20 kg is accelerated across a rough surface by a rope passing over a pulley as shown in Fig. 7.91 . The tension in the rope is 10.0 N , and the pulley is 10.0 cm above the block . The coefficient of friction is 0.4 .
(a) Determine the acceleration of block when x = 0.4 m .
(b) Find the value of x at which the acceleration becomes zero .

View Solution

