A professional diver of mass 60kg performs a dive from a platform 10m above the water surface. Find the magnitude of the average impact force experienced by him if the impact time is 1s on collision with water surface. Assume that the velocity of the diver just after enering the water surface is 4ms−1(g=10ms−2) .
240N
600N
300N
60N
The correct Answer is:B
To solve the problem of finding the magnitude of the average impact force experienced by the diver, we can follow these steps:
Step 1: Calculate the final velocity of the diver just before hitting the water.
We can use the equation of motion for this:
V=U+gt
Where:
- V = final velocity just before hitting the water
- U = initial velocity (which is 0 m/s since the diver starts from rest)
- g = acceleration due to gravity (10 m/s²)
- t = time of fall (which we need to calculate)
First, we need to calculate the time taken to fall 10 m using the equation:
h=12gt2
Rearranging gives:
t=√2hg=√2×1010=√2≈1.41 seconds
Now, substituting into the velocity equation:
V=0+10×1.41≈14.1 m/s
Step 2: Calculate the change in velocity (ΔV).
The change in velocity is given by:
ΔV=V−U
Where:
- V = final velocity just before hitting the water (14.1 m/s)
- U = initial velocity just before entering the water (4 m/s)
Thus,
ΔV=14.1−4=10.1 m/s
Step 3: Calculate the average impact force (F).
Using the formula for average impact force:
F=m⋅ΔVt
Where:
- m = mass of the diver (60 kg)
- ΔV = change in velocity (10.1 m/s)
- t = impact time (1 s)
Substituting the values:
F=60⋅10.11=606 N
Step 4: Round off the result.
Since the problem may require rounding, we can round 606 N to 600 N for simplicity.
Final Answer:
The magnitude of the average impact force experienced by the diver is approximately 600 N.
---
We can use the equation of motion for this:
V=U+gt
Where:
- V = final velocity just before hitting the water
- U = initial velocity (which is 0 m/s since the diver starts from rest)
- g = acceleration due to gravity (10 m/s²)
- t = time of fall (which we need to calculate)
h=12gt2
Rearranging gives:
t=√2hg=√2×1010=√2≈1.41 seconds
V=0+10×1.41≈14.1 m/s
The change in velocity is given by:
ΔV=V−U
Where:
- V = final velocity just before hitting the water (14.1 m/s)
- U = initial velocity just before entering the water (4 m/s)
ΔV=14.1−4=10.1 m/s
Using the formula for average impact force:
F=m⋅ΔVt
Where:
- m = mass of the diver (60 kg)
- ΔV = change in velocity (10.1 m/s)
- t = impact time (1 s)
F=60⋅10.11=606 N
Since the problem may require rounding, we can round 606 N to 600 N for simplicity.
The magnitude of the average impact force experienced by the diver is approximately 600 N.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -III
Explore 31 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:NCERT BASED QUESTION
Explore 33 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -I (C.W)
Explore 47 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - IV
Explore 41 Videos
Similar Questions
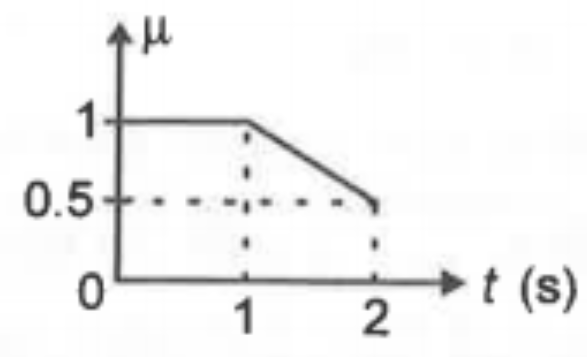
block is moving on a rough surface. At time t=0, speed of the block is 20 m/s. Coefficient of friction (μ) between block and surface varies with time (t) as shown in figure. The magnitude of velocity of particle after t = 2 second is (g=10ms−2)
View SolutionAn annular disc of radius r1=10cm and r2=5cm is placed on a water surface. Find the surface tension force on the disc if we want to pull it from water surface. Take coefficient of surface tension as σ=7×10−3N/m,g=10ms−12.

View Solution
Knowledge Check
A professional diver of mass 60 kg performs a dive from a platform 10 m above the water surface. Find the magnitude of the average impact force experienced by him if the impact time is 1s on collision with water surface. Assume that the velocity of the diver just after entering the water surface is 4ms−1.(g=10ms−2)
A240NB600NC300ND60NA diver makes 2.5 revolutions on the way from a 10−m−high platform to the water. Assuming zero initial vertical velocity, the average angular velocity during the dive is.
A3π√2rad/sB5π√2rad/sC5π√3rad/sDπ√2rad/sThere is a hole at the side-bottom of a big water tank. The area of the hole is 4mm2 to it a pipe is connected. The upper surface of water is 5 m above the hole. The rate of flow of water through the pipe is (in m3s−1)(g=10ms−2)
A4×10−5B4×105C4×10−6D28×10−5
A boy of mass 60kg is standing over a platform of mass 40kg placed over a smooth horizontal surface. He throws a stone of mass 1kg with velocity v=10m/s at an angle of 45∘ with respect to the ground. Find the displacement of the platform (with boy) on the horizontal surface when the stone lands on the ground. Take g=10m/s2.
View SolutionTwo particles of mass 2kg and 6kg are moving on smooth horizontal surface collides with each other.If velocity of their common centre of mass is 10m/s before collision then what will be the total linear momentum of system of particles after collision.(Assume they move along the surface after collision)
View SolutionA ball after falling a distance of 5 meter rest hits elastically the floor of a lift and rebounds. At the time of impact the lift was moving up with a velocity of 1m/sec. The velocity with which the ball rebounds just after impact is : (g=10m/sec2)
View SolutionA diver springs upward from a board that is three meters above the water. At the instant she contacts the water her speed is 8.90 m/s and her body makes an angle of 75.0∘ with respect to the horizontal surface of the water. Determine her initial velocity, both magnitude and direction.
View SolutionA body of mass 2kg moving on a horizantal surface with an initial velocity of comes to rest after 2 second. If one wants to keep this body moving on the same surface with a velocity of 4ms−1 the force required is
View Solution

