A chain of mass 'm' is attached at two points A and B of two fixed walls as shown in the Find the tension in the chain near the walls at point A and at the mid point C
 .
.
i) At point A
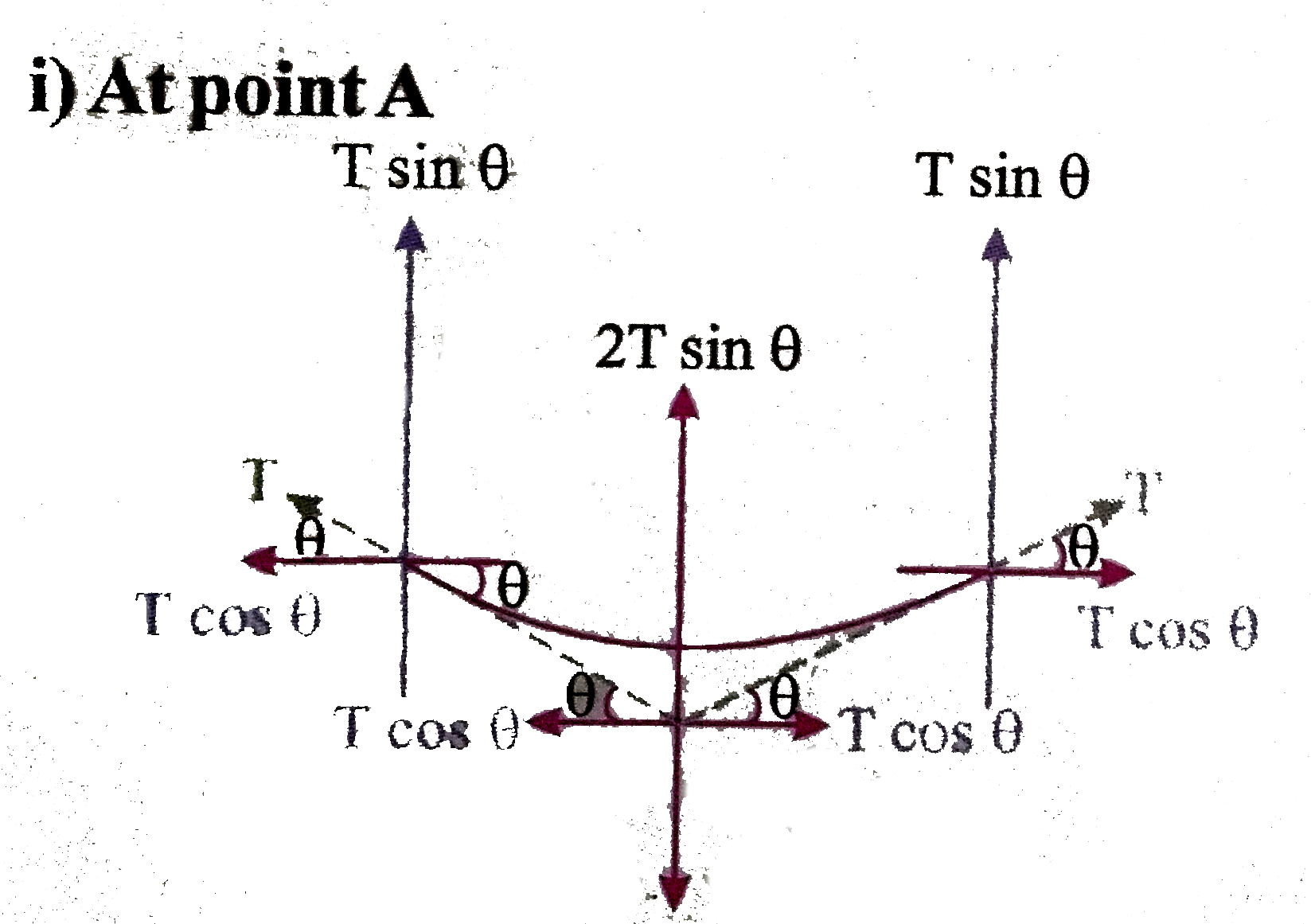
27sinθ=mg⇒T=12mgcosecθ
(ii) Tension along horizontal direction is same ev-erywhere
∵ (no external force is acting on it in horizontal di rection.)
At point C
T1=Tcosθ=mgcosθ2sinθ=mgcotθ2
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:C.U.Q
Explore 73 Videos
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:LEVEL -I (C.W)
Explore 47 Videos
- MOTION IN A STRAIGHT LINEBook:NARAYNAChapter:MOTION IN A STRAIGHT LINEExercise:Level 2 H.W
Explore 29 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:EXERCISE - IV
Explore 41 Videos
Similar Questions
A block of mass m is attached to a chain as shown in the diagram. Find the tension in each of the three chains. The ring and chains are light.

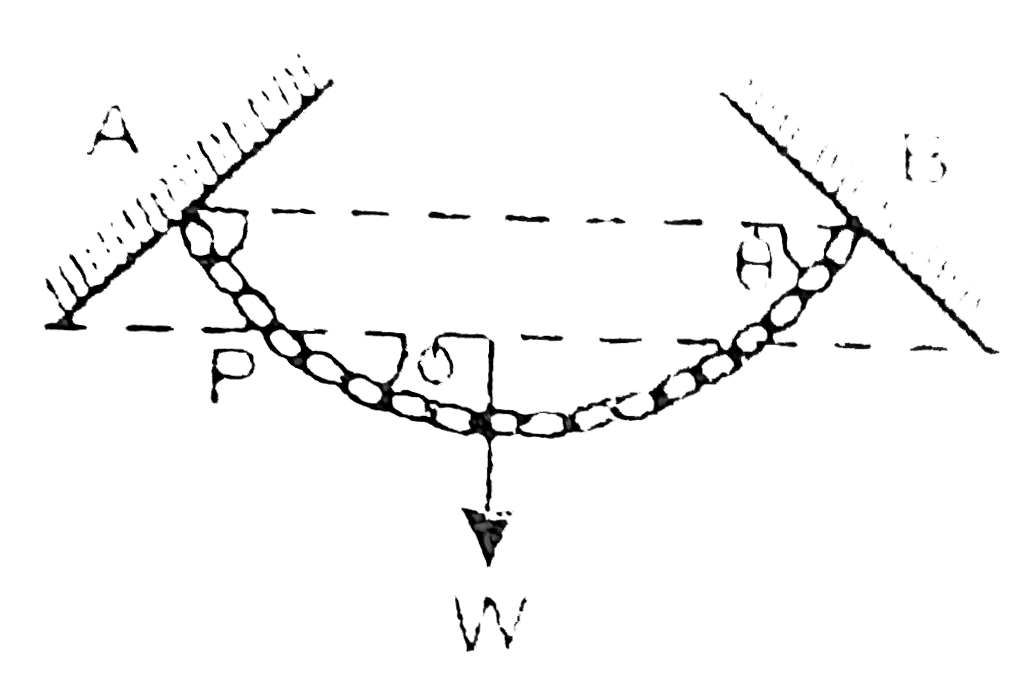
View SolutionA flexible chain of weight W hangs between two fixed points A and B at the same level. The inclination of the chain with the horizontal at the two points of support is θ. Calculated the tension of the chain at end points and also at the lower most point .
[Hints : Consider equilibrium of each half of the chain. ]
View Solution
Knowledge Check
A flexible chain of weight W hangs between two fixed points A and B at the same level. The inclination of the chain with the horizontal at the two points of support is θ=60∘. What is the tension of the chain at the point P where inclination of chain with horizonrtal is ϕ=30∘
 A2W3BW2CWDW3
A2W3BW2CWDW3A flexible chain of weight W hangs between two fixed points A & B which are at the same horizontal level. The inclination of the chain with the horizontal at both the points of support is θ . What is the tension of the chain at the mid point ?
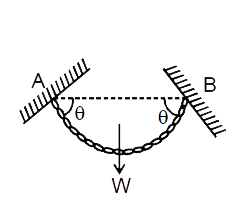 AW2cosecθBW2tanθCW2tanθDnone
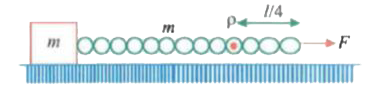
AW2cosecθBW2tanθCW2tanθDnoneA block of mass m is pulled by a uniform chain of mass m tied to it by applying a force F at the other end of the chain.The tension at a point P which is at a distance of quarter of the length of the chain from the free end,will be
 A3F4B7F8C6F7D4F5
A3F4B7F8C6F7D4F5
A block of mass M is attached to a uniform rope of mass m. This arrangement is pulled by applying a force F at the rope as shown. Find the tension in the rope (a) at the junction of the rope and the block (b) at the mid point of the rope.
View SolutionThe block shown in figure has a mass M and descends with an acceleration a. the mass of the string below the point A is m. Find the tension of the string at the point A and at the lower end.

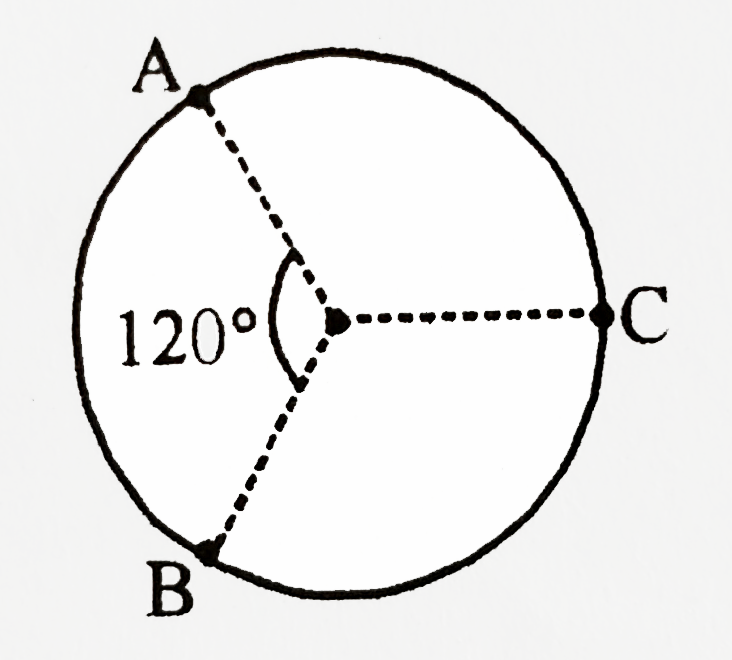
View SolutionA thin shell of mass m and radius R is fixed. Two particles of same mass m are fixed at point A and B on the shell such that AB subtends an angle of 120∘ at the centre. A particle of mass m is held at point C inside the shell which is on perpendicular bisector of line AB. Find the velocity of mass at C when it reaches the opposite end of the point C on the shell under the influence of gravitational field.
View SolutionA block of mass m is pulled by a uniform chain of mass m tied to it by applying a force F at the other end of the chain. The tension at a point P which is at a distance of quarter of the length of the chain from the free end, will be
View SolutionA chain of mass M and length L is held vertical by fixing its upper end to a rigid support. The tension in the chain at a distance y from the rigid support is:
View Solution

