A flexible chain of weight W hangs between two fixed points A and B at the same level. The inclination of the chain with the horizontal at the two points of support is θ. Calculated the tension of the chain at end points and also at the lower most point .
[Hints : Consider equilibrium of each half of the chain. ]
The correct Answer is:(i)W/2(2sinθ) (ii) W(cotθ)/2
To solve the problem of a flexible chain hanging between two fixed points A and B at the same level with an inclination of θ at the endpoints, we will analyze the forces acting on the chain and apply the principles of equilibrium.
1. Understanding the Setup:
- The chain has a total weight W and is suspended between two fixed points A and B.
- The angle of inclination with the horizontal at points A and B is θ.
- The chain can be considered to be in static equilibrium.
2. Dividing the Chain:
- We can divide the chain into two halves for analysis. Let’s consider one half of the chain from point A to the midpoint of the chain.
3. Forces Acting on the Half Chain:
- The weight of the half chain can be represented as W2 acting downwards at the midpoint.
- The tension at point A is denoted as T1 and at the midpoint as T2.
4. Resolving Tension into Components:
- The tension T1 at point A can be resolved into two components:
- Horizontal component: T1cos(θ)
- Vertical component: T1sin(θ)
5. Applying Equilibrium Conditions:
- For vertical equilibrium, the upward force must equal the downward force:
T1sin(θ)=W2
- For horizontal equilibrium, the horizontal components must balance:
T2=T1cos(θ)
6. Calculating Tension at Point A:
- From the vertical equilibrium equation, we can solve for T1:
T1=W2sin(θ)
7. Calculating Tension at the Midpoint:
- Substitute T1 into the horizontal equilibrium equation to find T2:
T2=T1cos(θ)=(W2sin(θ))cos(θ)=Wcos(θ)2sin(θ)
8. Final Results:
- The tension at the endpoints (point A and point B) is:
T1=W2sin(θ)
- The tension at the lowest point (midpoint) is:
T2=Wcos(θ)2sin(θ)
Summary of Results:
- Tension at endpoints T1=W2sin(θ)
- Tension at the lowest point T2=Wcos(θ)2sin(θ)
- The chain has a total weight W and is suspended between two fixed points A and B.
- The angle of inclination with the horizontal at points A and B is θ.
- The chain can be considered to be in static equilibrium.
- We can divide the chain into two halves for analysis. Let’s consider one half of the chain from point A to the midpoint of the chain.
- The weight of the half chain can be represented as W2 acting downwards at the midpoint.
- The tension at point A is denoted as T1 and at the midpoint as T2.
- The tension T1 at point A can be resolved into two components:
- Horizontal component: T1cos(θ)
- Vertical component: T1sin(θ)
- For vertical equilibrium, the upward force must equal the downward force:
T1sin(θ)=W2
- For horizontal equilibrium, the horizontal components must balance:
T2=T1cos(θ)
- From the vertical equilibrium equation, we can solve for T1:
T1=W2sin(θ)
- Substitute T1 into the horizontal equilibrium equation to find T2:
T2=T1cos(θ)=(W2sin(θ))cos(θ)=Wcos(θ)2sin(θ)
- The tension at the endpoints (point A and point B) is:
T1=W2sin(θ)
- The tension at the lowest point (midpoint) is:
T2=Wcos(θ)2sin(θ)
- Tension at endpoints T1=W2sin(θ)
- Tension at the lowest point T2=Wcos(θ)2sin(θ)
Topper's Solved these Questions
- MOMENT, TORQUE, EQUILIBRIUM OF BODIESBook:NN GHOSHChapter:MOMENT, TORQUE, EQUILIBRIUM OF BODIESExercise:Exercises
Explore 33 Videos
- LAWS OF MOTION, FREE BODY DIAGRAMBook:NN GHOSHChapter:LAWS OF MOTION, FREE BODY DIAGRAMExercise:Exercise (B)
Explore 34 Videos
- ROTATIONAL DYNAMICS, MOMENT OF INERTIABook:NN GHOSHChapter:ROTATIONAL DYNAMICS, MOMENT OF INERTIAExercise:Exercises
Explore 42 Videos
Similar Questions
A chain of mass 'm' is attached at two points A and B of two fixed walls as shown in the Find the tension in the chain near the walls at point A and at the mid point C
 .
.
View SolutionA heavy particle of mass 2kg is tied to two strings, each of length 25 cm and they are tied to two points 30 cm apart on the same vertical line. The particle is whirled in a horizontal plane with a speed of 1.8ms−1. Calculate the ratio of the tensions of the two strings.
View Solution
Knowledge Check
A flexible chain of weight W hangs between two fixed points A & B which are at the same horizontal level. The inclination of the chain with the horizontal at both the points of support is θ . What is the tension of the chain at the mid point ?
 AW2cosecθBW2tanθCW2tanθDnone
AW2cosecθBW2tanθCW2tanθDnoneA flexible chain of weight W hangs between two fixed points A and B at the same level. The inclination of the chain with the horizontal at the two points of support is θ=60∘. What is the tension of the chain at the point P where inclination of chain with horizonrtal is ϕ=30∘
 A2W3BW2CWDW3
A2W3BW2CWDW3In the arrangement shown in figure, coefficient of friction between two fixed points A & B which are at the same horizontal level. The inclination of the chain with the horizontal at both the points of support is θ. What is the tension of the chain at the mid point?
 A8 NB10 NC6 ND4 N
A8 NB10 NC6 ND4 N
A chain of length L supported at the upper end is hanging vertically. It is released. Determine the interval of time it takes the chain to pass a point 2L below the point of support, if all of the chain is a freely falling body.
View SolutionA uniform cable has a mass of 100 kg and is suspended between two fixed points A and B, at the same horizontal level. At the support points the cable makes angles of as shown in figure. Choose the correct option. (g = 10 m/s2)
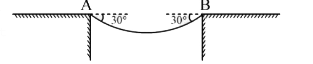
View SolutionA weight w is sasponded from the mid -point of a tope whose ends are at the same level In after in make the rope perfectly horizontalthe force applied to each of its ends must be
View SolutionA block of mass m is pulled by a uniform chain of mass m tied to it by applying a force F at the other end of the chain. The tension at a point P which is at a distance of quarter of the length of the chain from the free end, will be
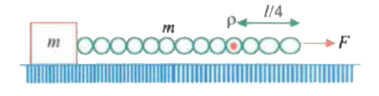
View SolutionA 40kg child sits on a swing supported by two chains,each 3 m long. If the tension in each chain at lowest point in 350 N, then the child's speed at the lowest point is [Take g=10m/s2]
View Solution

