The ratio of the amplitudes of the simple harmonic oscillations given by y1=Asinωt and
A
1
B
2
C
1/√2
D
√2
Video Solution
Text Solution
The correct Answer is:D
y1=Asinωt (i)
y2=A2sinωt+A2cosωt
=A2sinωt+A2sin(π2+ωt)
=A′sin(ωt+θ)
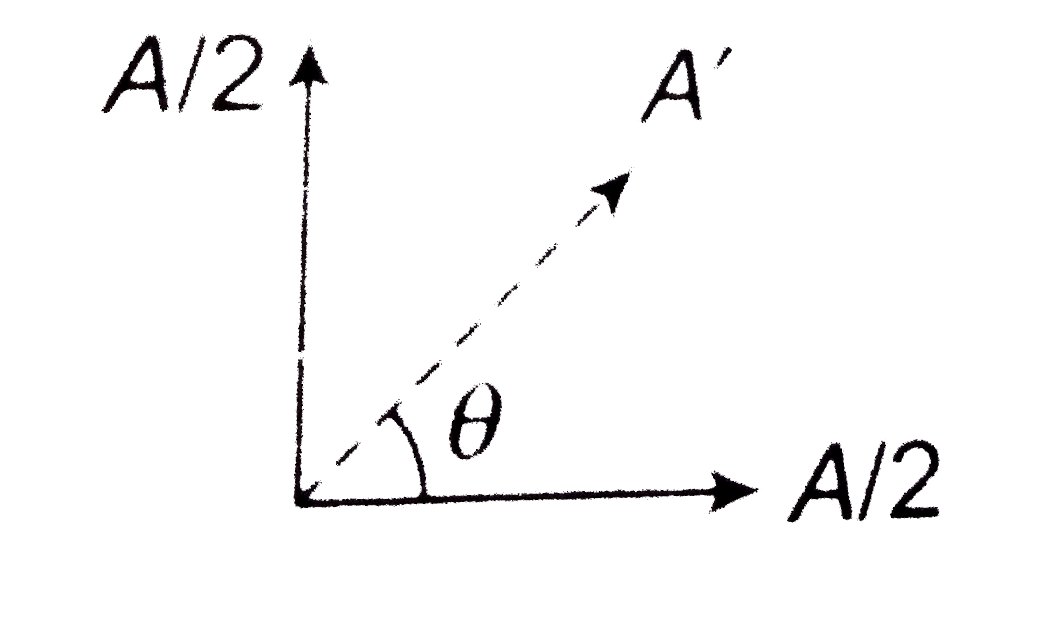
A′=√2.A2=A√2
θ=45∘=π/4
y2=A√2sin(ωt+π/4)
AA′=AA/√2=√2
OR
y2=A2sinωt+A2cosωt=A2(sinωt+cosωt)
=A2√2(1√2sinωt+1√2cosωt)
=A2√2(sinωtcosπ/4+cosωtsinπ/4)
=A√2sin(ωt+π/4)
Note: asinθ+bcosθ (can be converted into a single term as)
=√a2+b2(a√a2+b2sinθ+b√a2+b2cosθ)
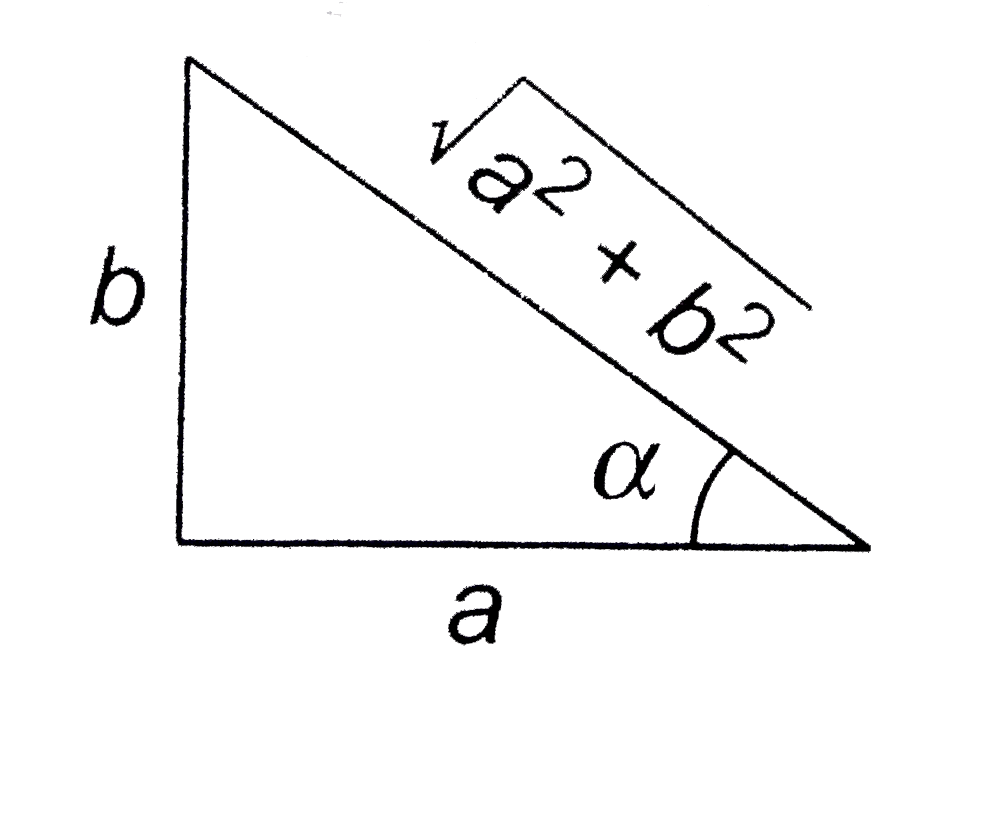
=√a2+b2(sinθcosθ+cosθsinα)
=√a2+b2sin(θ+α)
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Simple harmonic oscillations are
Aone dimensionalBthree dimensionalCtwo dimensionalDfour dimensionalThe phase of simple harmonic oscillator is
Aexpressed in timeBexpressed in angleCexpressed in distanceDa' and 'b'The amplitude of given simple harmonic motion is y=(3sinωt+4cosωt)m
A1 mB3 mC4 mD5 m
Assertion: If the amplitude of a simple harmonic oscillator is doubled, its total energy becomes double.
Reason: The toal energy is directly proportional to the amplitude of vibration of the harmonic oscillator.
View SolutionThe displacement of a particle executing simple harmonic motion is given by
y=A0+Asinωt+Bcosωt
Then the amplitude of its oscillation is given by :
View SolutionIn a simple harmonic oscillator, at the mean position
View SolutionThe displacement of a particle executing simple harmonic motion is given by y=A0+Asinωt+Bcosωt. Then the amplitude of its oscillation is given by
View SolutionIn. a simple harmonic oscillator, at the mean position
View Solution
