A homogeneous rod AB of length L = 1.8 m and mass M is pivoted at the center O in such a way that it can rotate it can rotate freely position. An insect S of the same mass M falls vertically with speed V on the point C, midway between the points O and B. Immediately after falling, the insect moves towards the end B such that the rod rotates with a constant angular velocity omega.
(a) Determine the angular velocity ω in terms of V and L.
(b) If the insect reaches the end B when the rod has turned through an angle of 90∘, determine V.
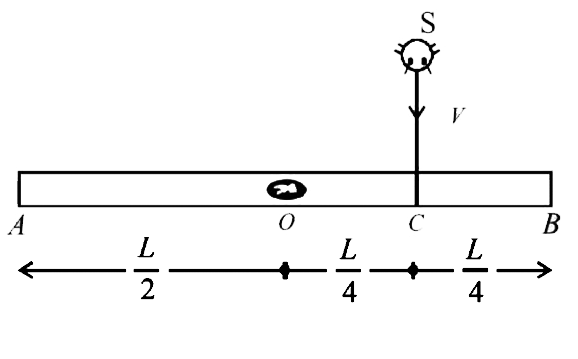
Let the angular velocity be ω, when the insect strikes the rod at C.
By the conservation OˆI angular momentum about C
MvL4=I0ω=[ML212+M(L4)2]ω
=748ML2ω
ω=12v7L
Topper's Solved these Questions
Similar Questions
A block of mass m is connected to a light rod of length l . One end of the rod is pivoted to a point in such a way that it can be rotated in a vertical plane . Initially rod is vertical with the block a its lowest position . If velocity given to the block is √ngl then it is found to complete the circle successfully . Find the value of n .
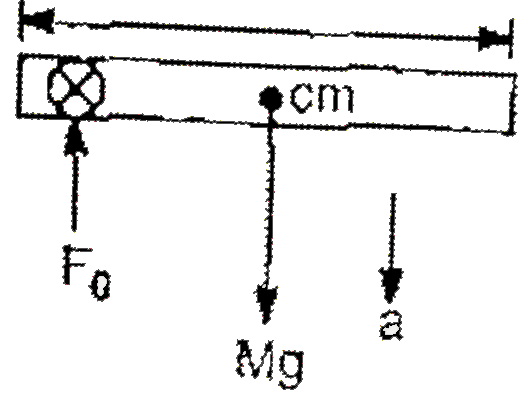
View SolutionA uniform slender rod of length L and mass M is pivoted at one end. It is held horizontal and releasaed. Assume the pivot is frictionless. Find .
(a) the angular acceleration of the rod immediately after it is released, and
(b) the force F0 exerted on the rod by the pivot immediately after release.
View Solution
Knowledge Check
A thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
Acentrifugal force acting on rod is mL2sinθω2 and will pass through centre of massBcentrifugal force acting on rod is mL2sinθω2 and will not pass through centre of massCθ=cos−1(3g2ω2L)Dθ=cos−1(gω2L)Moment of inertia of a rod of mass M and length L about an axis passing through a point midway between centre and end is
AML26BML212C7ML224D7ML248
A uniform rod of length L and mass m is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass m is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling isA3mg2B2mgCzeroDmg2
A rod of mass m,length l pivoted at its centre is free to rotate in a vertical plane.The rod is at rest and is in vertical position.A bullet of mass m/2 moving horizontally with speed v strikes and sticks to one end of the rod. Angular velocity of system just after collision is
View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View Solution
A uniform rod AB of length L and mass m is suspended freely at A and hangs vertically at rest when a particle of same mass m is fired horizontally with speed v to strike the rod at its mid point. If the particle is brought to rest after the impact. Then the impulsive reaction at A is horizontal direction is
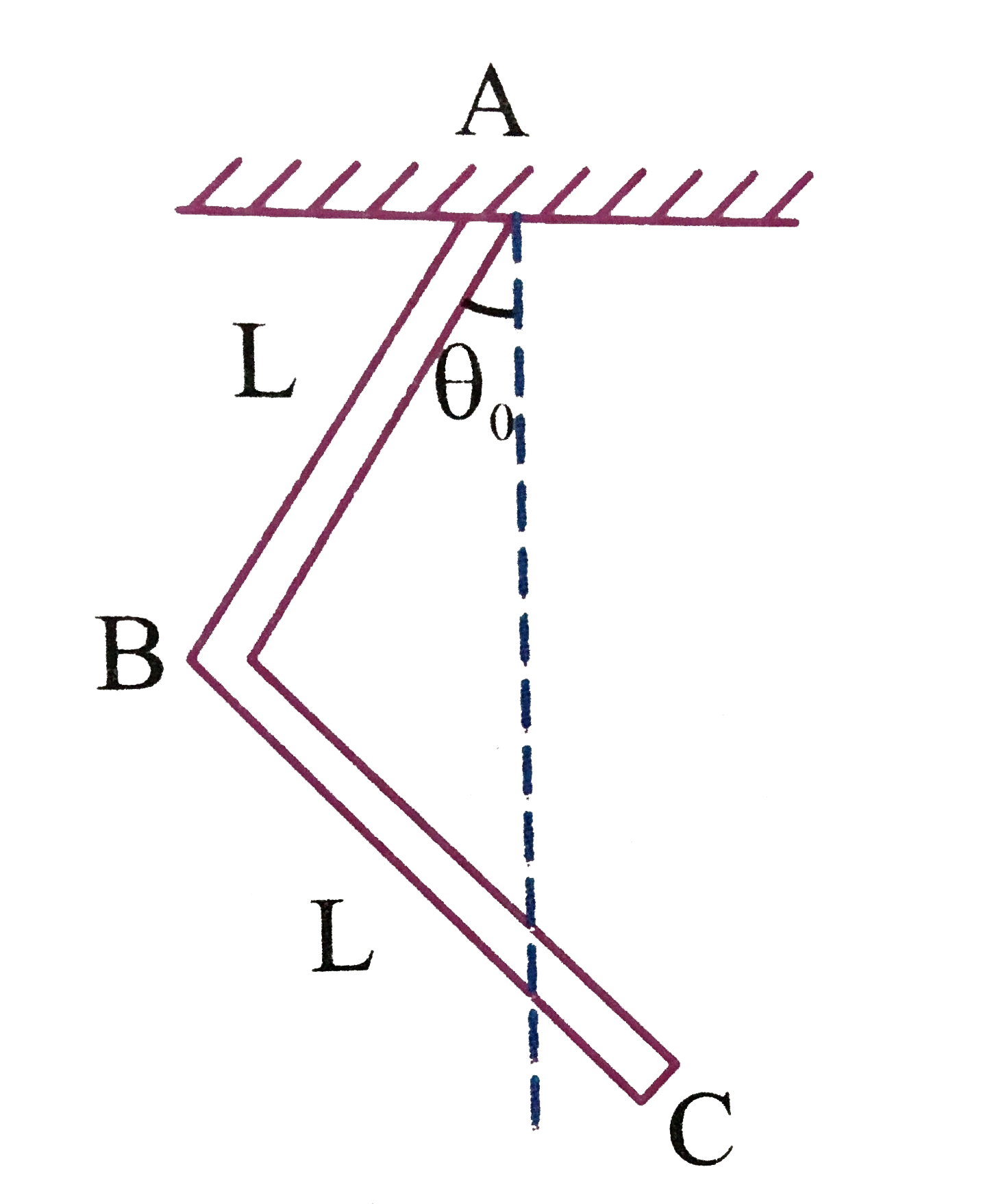
View SolutionA L-shaped bar of mass M is pivoted at one of its end so that it can freely rotate in a vertical plane as shwon. If it is slightly displaced from its equilibrium position then the frequency of oscillation is…….
View SolutionA rod of mass m and length 2R can rotate about an axis passing through O invertical plane.A disc of mass m and radius R/2 is hinged to the other end P ofthe rod and can freely rotate about P. When disc is at lowest point both rod and disc has angular velocity ω. If rod rotates by maximum angleθ=60∘ with downward vertical, then ω interms of R and g will be(all hinges are smooth)

View Solution