A block of mass m is connected to a light rod of length l . One end of the rod is pivoted to a point in such a way that it can be rotated in a vertical plane . Initially rod is vertical with the block a its lowest position . If velocity given to the block is √ngl then it is found to complete the circle successfully . Find the value of n .
The correct Answer is:D
To solve the problem step-by-step, we will analyze the energy conservation between the lowest point (point A) and the highest point (point B) of the circular motion of the block attached to the rod.
Step 1: Understand the System
We have a block of mass m attached to a light rod of length l that can rotate in a vertical plane. Initially, the rod is vertical, and the block is at the lowest position. The block is given an initial velocity of √ngl.
Step 2: Identify Points A and B
- Point A: The lowest point where the block is given the initial velocity.
- Point B: The highest point in the circular motion.
Step 3: Write the Energy Conservation Equation
According to the principle of conservation of mechanical energy:
Total Energy at A=Total Energy at B
This can be expressed as:
KEA+PEA=KEB+PEB
Step 4: Calculate Energies at Point A
At point A:
- Kinetic Energy KEA=12mv2=12m(√ngl)2=12mngl
- Potential Energy PEA=0 (taking the lowest point as the reference level)
Thus, the total energy at point A is:
EA=12mngl+0=12mngl
Step 5: Calculate Energies at Point B
At point B (the highest point):
- Kinetic Energy KEB=0 (for the block to just complete the circle, the velocity at the highest point should be 0)
- Potential Energy PEB=mg(2l) (the height at point B is 2l)
Thus, the total energy at point B is:
EB=0+mg(2l)=2mgl
Step 6: Set the Energies Equal
Now, set the total energy at point A equal to the total energy at point B:
12mngl=2mgl
Step 7: Simplify the Equation
We can cancel mgl from both sides (assuming m,g,l≠0):
12n=2
Step 8: Solve for n
Multiply both sides by 2:
n=4
Final Answer
The value of n is 4.
---
We have a block of mass m attached to a light rod of length l that can rotate in a vertical plane. Initially, the rod is vertical, and the block is at the lowest position. The block is given an initial velocity of √ngl.
- Point A: The lowest point where the block is given the initial velocity.
- Point B: The highest point in the circular motion.
According to the principle of conservation of mechanical energy:
Total Energy at A=Total Energy at B
This can be expressed as:
KEA+PEA=KEB+PEB
At point A:
- Kinetic Energy KEA=12mv2=12m(√ngl)2=12mngl
- Potential Energy PEA=0 (taking the lowest point as the reference level)
EA=12mngl+0=12mngl
At point B (the highest point):
- Kinetic Energy KEB=0 (for the block to just complete the circle, the velocity at the highest point should be 0)
- Potential Energy PEB=mg(2l) (the height at point B is 2l)
EB=0+mg(2l)=2mgl
Now, set the total energy at point A equal to the total energy at point B:
12mngl=2mgl
We can cancel mgl from both sides (assuming m,g,l≠0):
12n=2
Multiply both sides by 2:
n=4
The value of n is 4.
Topper's Solved these Questions
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Chapter Practice Test
Explore 16 Videos
- WORK, ENERGY AND POWER Book:MODERN PUBLICATIONChapter:WORK, ENERGY AND POWER Exercise:Objective Type Questions (Matrix Match Type Questions)
Explore 2 Videos
- WAVESBook:MODERN PUBLICATIONChapter:WAVESExercise:CHAPTER PRACTICE TEST
Explore 14 Videos
Similar Questions
One end of a light rod is clamped in such a manner that rod can be rotated in a vertical plane . A block of mass mis attached to the other ened of rod and the block stays at rest at its lowest position . What minimum speed should be imparted to the bock so that it may complete its circle ? Assume length of rod to be l .
View SolutionA light rigid rod has a bob of mass m attached to one of its end. The other end of the rod is pivoted so that the entire assembly can rotate freely in a vertical plane. Initially, the rod is held vertical as shown in the figure. From this position it is allowed to fall. (a) When the rod has rotated through θ=30∘ , what kind of force does it experience– compression or tension? (b) At what value of θ the compression (or tension) in the rod changes to tension (or compression)?
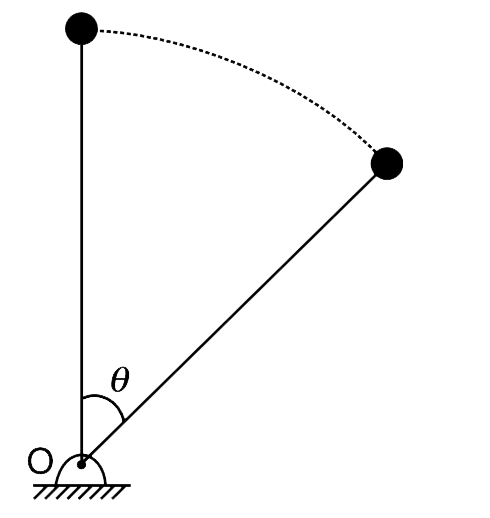
View Solution
Knowledge Check
One end of a light rod of length 1m is attached with a string of length 1m. Other end of the rod is attached at point O such that rod can move in a vertical circle. Other end of the string is attached with a block of mass 2kg. The minimum velocity that must be given to the block in horizontal direction so that it can complete the vertical is (g=10m/s2)
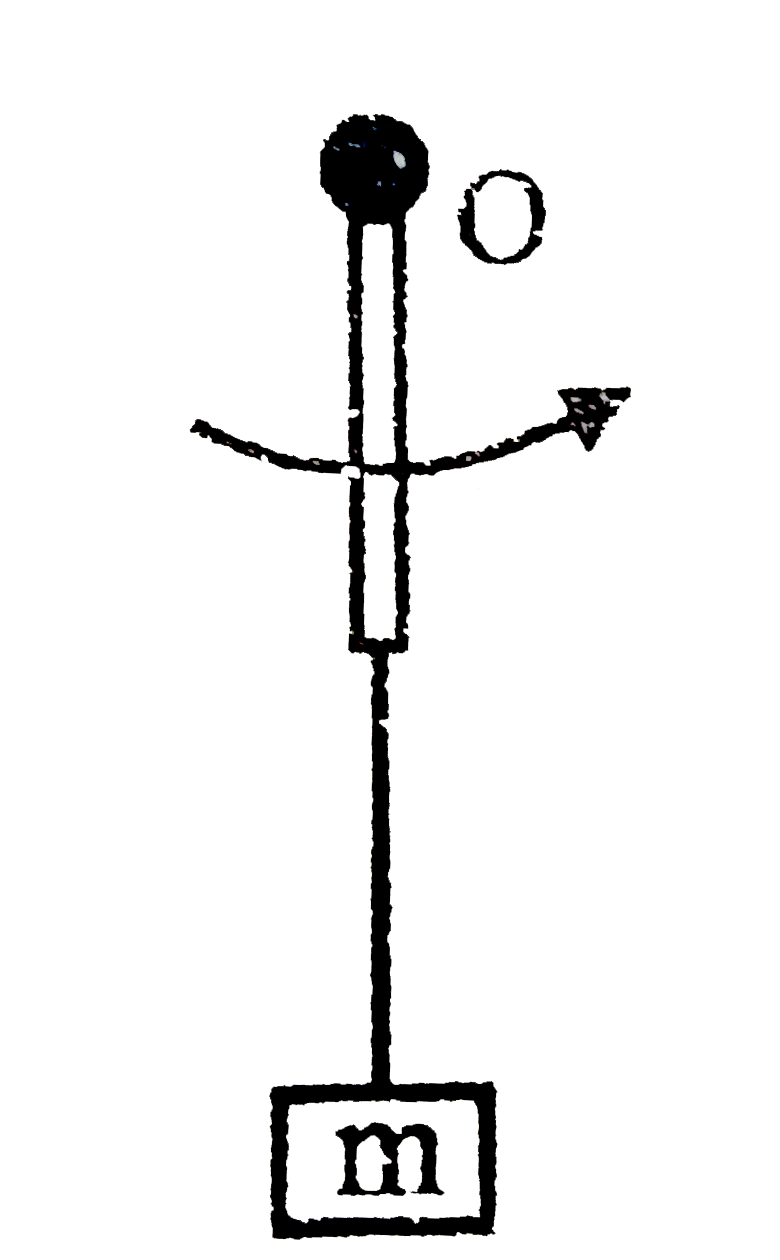 A4√5B5√5C10D3√5
A4√5B5√5C10D3√5A particle of mass m is fixed to one end of a light rigid rod of length l and rotated in a vertical circular path about its other end. The minimum speed of the particle at its highest point must be
AzeroB√glC√1.5glD√2glA rod of mass M and length L is made to stand vertically. Potential energy of the rod in this position is
AMglBMgl2CMgl3DMgl4
A uniform rod of mass M and length L with two particles m and m2 attached to its ends, is pivoted at its centre. The system rotates in a vertical plane with angular velocity ω.

View SolutionTwo point masses m are connected the light rod of length l and it is free to rotate in vertical plane as shown in figure. Calculate the minimum horizontal velocity is given to mass so that it completes the circular motion in vertical lane.
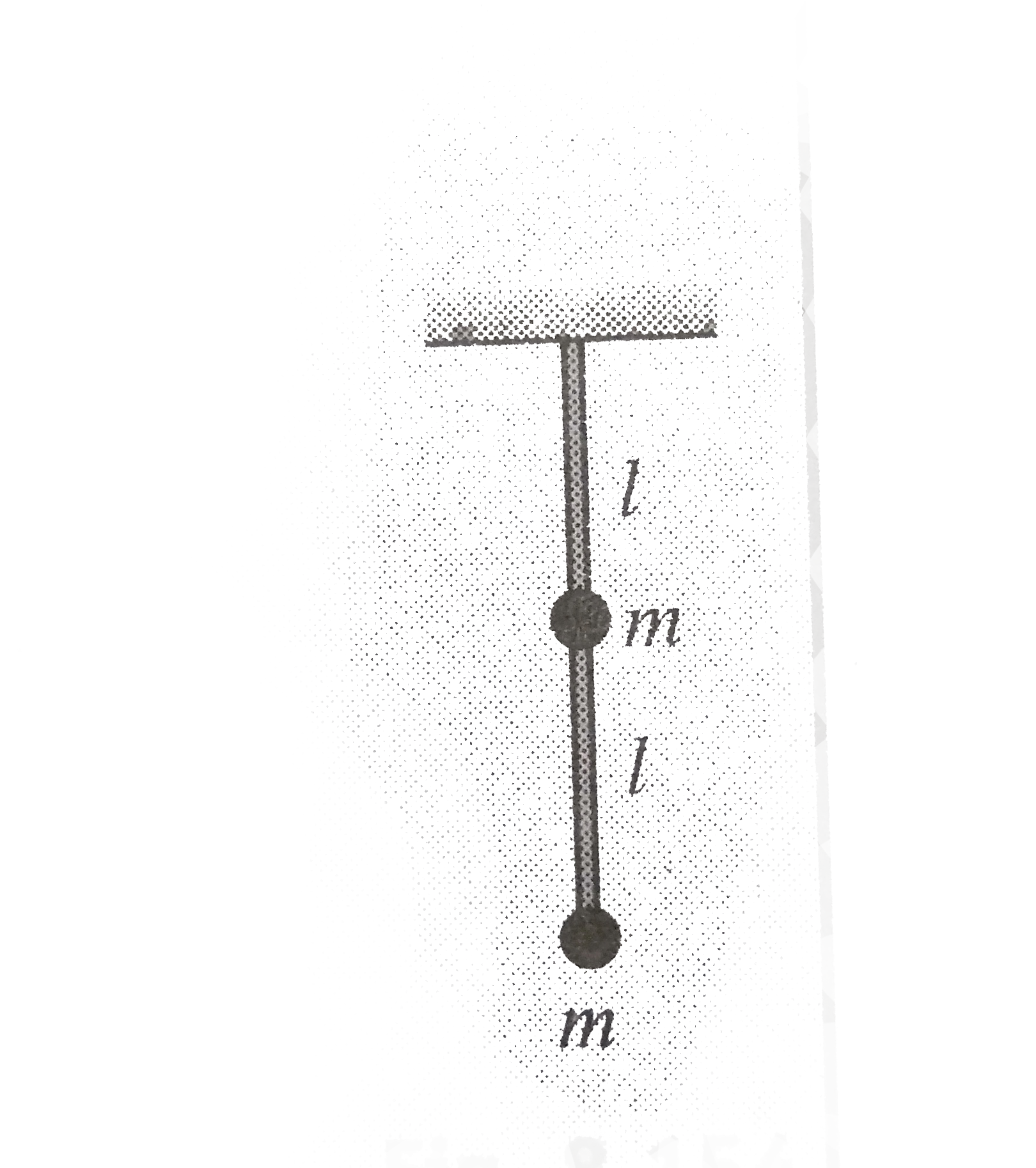
View SolutionA rod of length l is released from the vertical position on a smooth horizontal plane. What is the nature of motion of the free end of the rod ?
View SolutionA slender uniform rod of mass M and length l is pivoted at one ens so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is
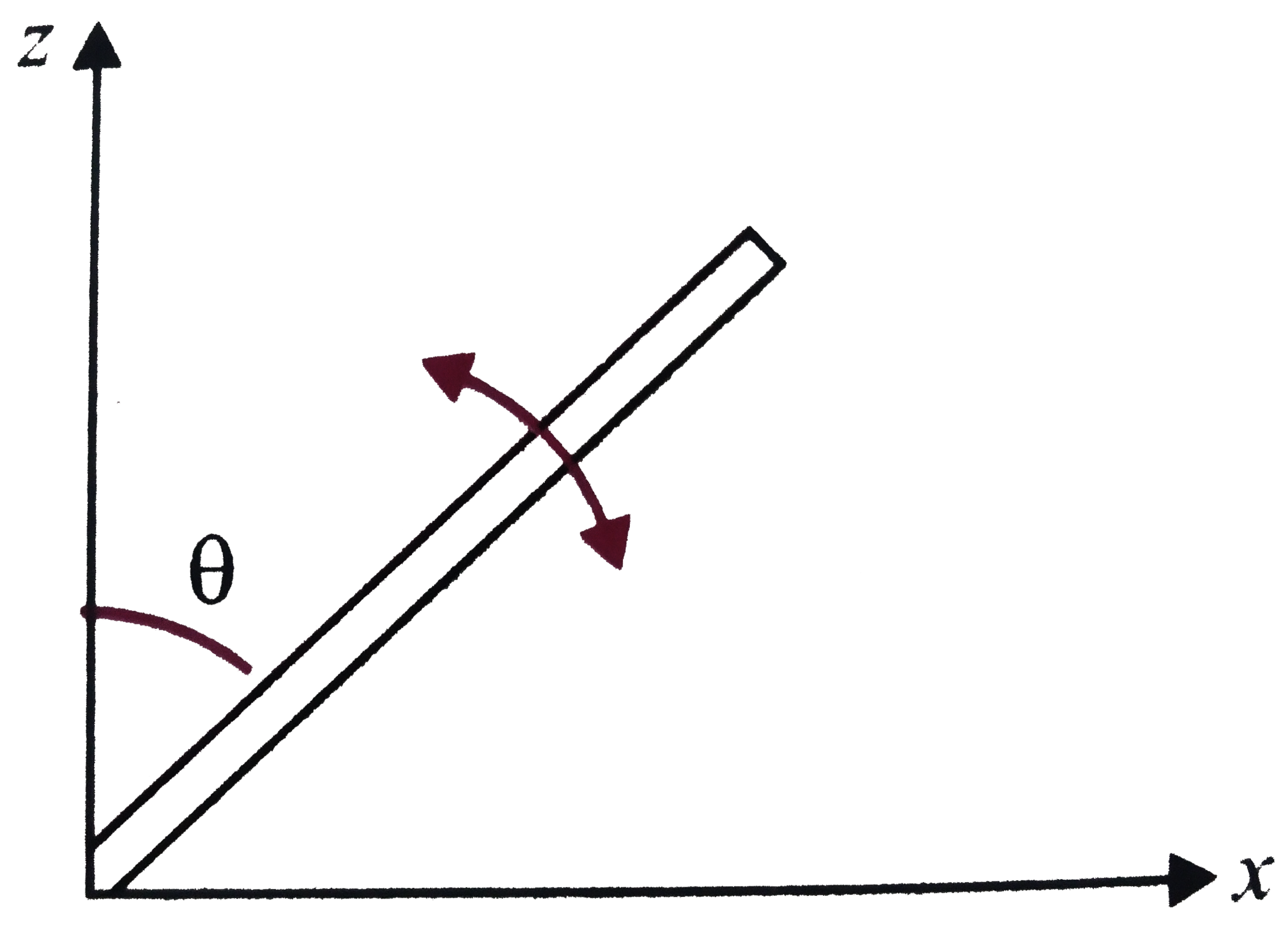
View SolutionA particle of mass m is fixed to me one end of a light right rod of length l and rotated in a vertical circular path about its other end. The minmum speed of the particle at its highest point must be
View Solution

