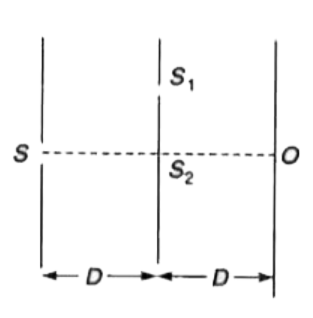
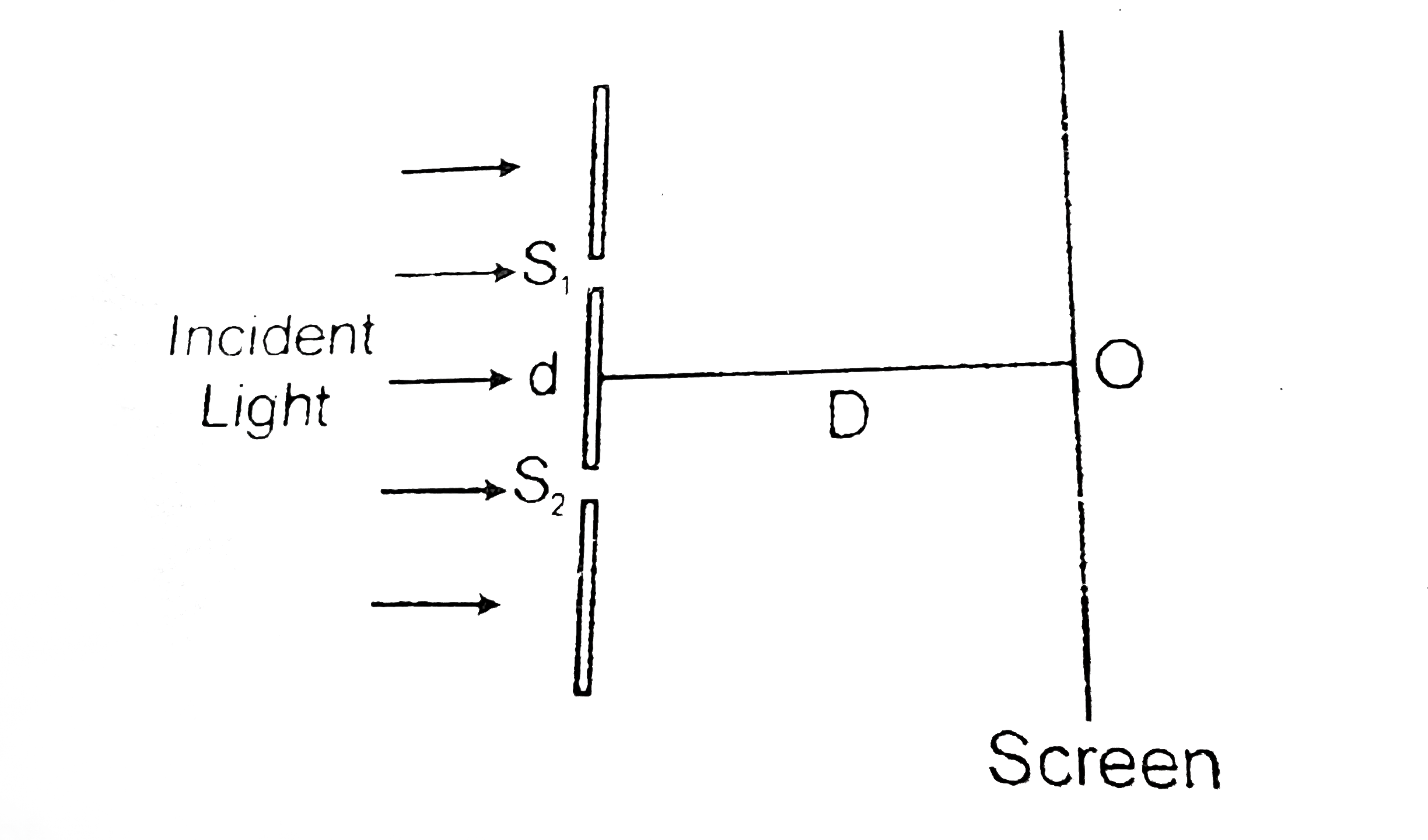
A screen is at distance D=80 cm form a diaphragm having two narrow slits S1 and S2 which are d=2 mm apart.
Slit S1 is covered by a transparent sheet of thickness
t1=2.5μm slit S2 is covered by another sheet of thikness
t2=1.25μm as shown if Fig. 2.52.
Both sheets are made of same material having refractive index μ=1.40
Water is filled in the space between diaphragm and screen. Amondichromatic light beam of wavelength λ=5000Å is incident normally on the diaphragm.
Assuming intensity of beam to be uniform, calculate ratio of intensity of C to maximum intensity of interference pattern obtained on the screen (μw=4/3)

The correct Answer is:3/4
Path difference Δx=μmt1+μl(S1C−t1)−[μmt2+μl(S2C−t2)]
Δx=μm(t1−t2)−μlt1+μ1t2
Δx=μm(t1−t2)−μl(t1−t2) ltbr Δx=(μm−μl)(t1−t2)
Δx=(1.4−43)(2.5×10−6−1.25×10−6)
Δx=0.23×1.25×10−6
Δx=2.53×10−7m
Δx=25003Å=50006Å
Δ=λ6
phase difference ϕ=π3
ϕ=60∘
Resultant intensity IC=I+I+2√I×Icos60∘
IC=3I
Imax=I+I+2I
Imax=4I
ICImax=34
Similar Questions
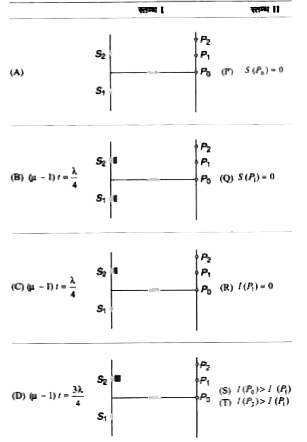
स्तम्भ I में स्टैण्डर्ड यंग द्वि - स्लिट विन्यास की चार परिस्थितयाँ दिखाई गई है | जिनमें स्लिट S1 तथा S2 स्क्रीन से काफी दूरी पर है | प्रत्येक परिस्थिति में S1P0=S2P0,S1P1−S2P1=λ/4 और S1P2−S2P2=λ/3, जहाँ λ प्रकाश की तरंगदैर्ध्य है | B, C व D परिस्थितियों में स्लिट S1 के सामने μ अपवर्तनांक और t मोटाई की पारदर्शी शीट रखी गई है | इन सीटों की मोटाई प्रत्येक परिस्थिति में भिन्न - भिन्न है | स्क्रीन के किसी बिंदु P पर दोनों स्लिट से पहुँच रही प्रकाश तरंगों के फेज - अंतर को S( P ) से निरूपित किया गया है | तथा प्रकाश की तीव्रता को I ( P ) से निरूपित किया गया है | स्तम्भ I की प्रत्येक परिस्थितियों के लिए स्तम्भ II के प्रकथनों को आपस में मिलाइए |
View SolutionIn Young's double slit experiment S1 and S2 are two slits. Films of thickness t1 and t2 and refractive indices μ1 and μ2 are placed in front of S1 and S2 respectively. If μ1t1=μ2t2, then the central maximum will :
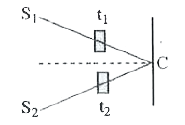
View Solutionदो आदर्श स्लिटो S1 व S2 को एक λ तरंगदैर्ध्य वाले आदर्श स्लिट स्त्रोत S द्वारा प्रकाशित किया जाता है। स्लिट S चित्रानुसार S2 के ठीक पीछे स्थित है। स्त्रोत स्लिट S एवं (S1,S2) स्लिटो के तलो के बीच की दूरी D है। एक पर्दा स्लिटो के तल से D दूरी पर स्थित है। स्लिटो (S1,S2) के बीच की दूरी (d) का न्यूनतम मान क्या होना चाहिए ताकि बिंदु O पर अदीप्त फ्रिन्ज प्राप्त हो?
View SolutionIn Young.s double slit experiment S1 andS2 are two slits. Films of thicknesses t1 and t2 refractive indices μ1andμ2 are placed in front ofS1andS2 repectively. If μ1t1=μ2t2 , then the central maximum will
View SolutionA screen is at distance D = 80 cm form a diaphragm having two narrow slits S_(1) and S_(2) which are d = 2 mm apart. Slit S_(1) is covered by a transparent sheet of thickness t_(1) = 2.5 mu m slit S_(2) is covered by another sheet of thickness t_(2) = 1.25 mu m as shown if Fig. 2.52. Both sheets are made of same material having refractive index mu = 1.40 Water is filled in the space between diaphragm and screen. A monochromatic light beam of wavelength lambda = 5000 Å is incident normally on the diaphragm. Assuming intensity of beam to be uniform, calculate ratio of intensity of C to maximum intensity of interference pattern obtained on the screen (mu_(w) = 4//3)
View Solutionएक श्वेत प्रकाश स्रोत द्वारा प्रकाशित दो रेखाछिद्र S1 और S2 एक श्वेत केंद्रीय उच्चिष्ठ बनाते हैं।
1. 25 अपवर्तनांक और t1 मोटाई की एक पारदर्शी शीट को S1 के सामने रखा गया है। 1.50 अपवर्तनांक और t2 मोटाई की एक अन्य पारदर्शी शीट को S2 के सामने रखा गया है। यदि केंद्रीय उच्चिष्ठ प्रभावित नहीं होता है, तो अनुपात t1:t2 होगा:
View SolutionFigure shows a YDSE setup having identical slits S_(1) and S_(2) with d =5 mm and D = 1 m. A monochromatic light of wavelength lamda = 6000 Å is incident on the plane of slit due to which at screen centre O, an intensity I_(0) is produced with fringe pattern on both sides Now a thin transparent film of 11 mu m thickness and refractive index mu = 2.1 is placed in front of slit S_(1) and now interference patten is observed again on screen. After placing the film of slit S_(1) , the intensity at point O screen is :
View SolutionFigure shows a YDSE setup having identical slits S1 and S2 with d =5 mm and D = 1 m. A monochromatic light of wavelength λ=6000Å is incident on the plane of slit due to which at screen centre O, an intensity I0 is produced with fringe pattern on both sides Now a thin transparent film of 11μm thickness and refractive index μ=2.1 is placed in front of slit S1 and now interference patten is observed again on screen.
After placing the film of slit S1, the intensity at point O screen is :
View Solution
