In a YDSE two him transparent sheet are used in front of the slits & having and respectively.If both sheets have thickness ,the central maximum is observed at a distance of from center.Now the sheets are replaced by another two sheets each of refractive index but having thickness .Now central maximum is observed at distance of from center on the same side as before.Find the thickness (inm) [Given:d=1mm,D=1m]
![In a YDSE two him transparent sheet are used in front of the slits S(1)&S(2) having mu(1)=1.6and mu(2)=1.4 respectively.If both sheets have thicknesst ,the central maximum is observed at a distance of 5mmfrom centerO.Now the sheets are replaced by another two sheets each of refractive index (mu(1)-mu(2))/(2) but having thickness t(1)&t(2)=(t(1)-t(2))/(2).Now central maximum is observed at distance of 8mm from centerO on the same side as before.Find the thickness t(1) (inmum) [Given:d=1mm,D=1m]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/NG_PHY_WO_C02_E01_025_Q01.png)
The correct Answer is:
Path difference =
For central maximum at , path difference=
since
Now path difference =
For central maximum path difference=
Given that
from(2)&(3)
Similar Questions
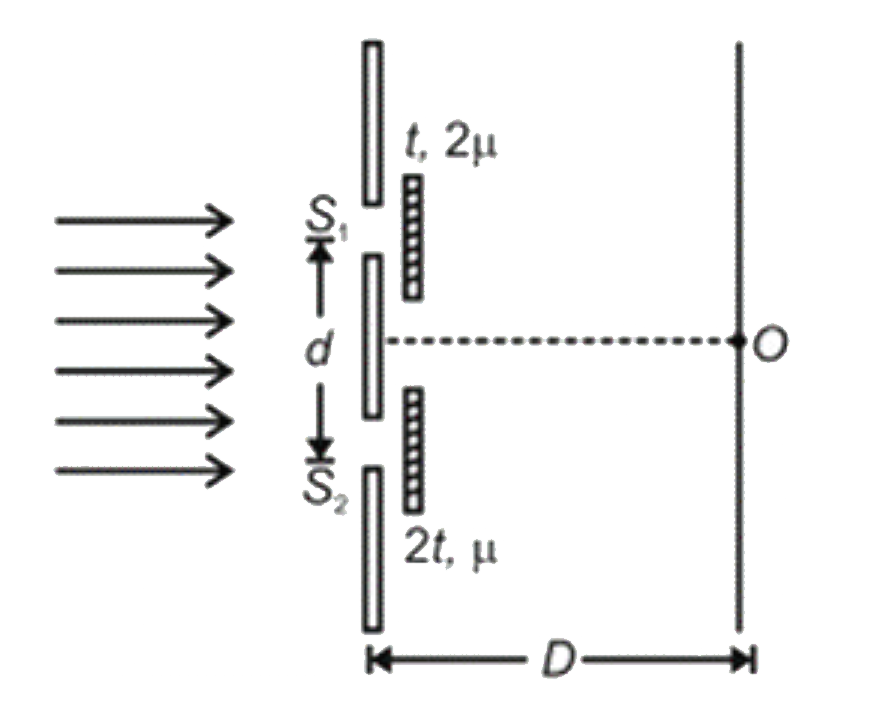
In the YDSE shown below, two slits are covered with thin sheets having a thickness t and 2t and refractive indices 2μ and μ respectively. The position of central maxima is shifted by a distance of N (in cm) from the central position of the screen. Find the value of N.
[d=1mm,D=1m,t=2×10−2mm,μ=32]
View SolutionIn YSDE, both slits are covered by transparent slab. Upper slit is covered by slab of R.I. 1.5 and thickness t and lower is
covered by R.I. 43 and thickness 2t, then central maxima

View Solution
Knowledge Check
If a ray of light takes t1 and t2 times in two media of absolute refractive indices μ1 and μ2 respectively to travel same distance, then
Aμ1t1=μ2t2Bμ1t2=μ2t1Ct1√μ1=t2√μ2Dt1√μ2=t2√μ1Two slits S1 and S2 illuminated by a white light source give a white central maxima. A transparent sheet of refractive index 1.25 and thickness t1 is placed in front of S1. Another transparent sheet of refractive index 1.50 and thickness t2 is placed in front of S2. If central maxima is not effected, then ratio of the thickness of the two sheets will be :
A1:2B2:1C1:4D4:1To make the central fringe at the centerO , mica sheet of refractive index 1.5 is introduced Choose the corect statement(S).
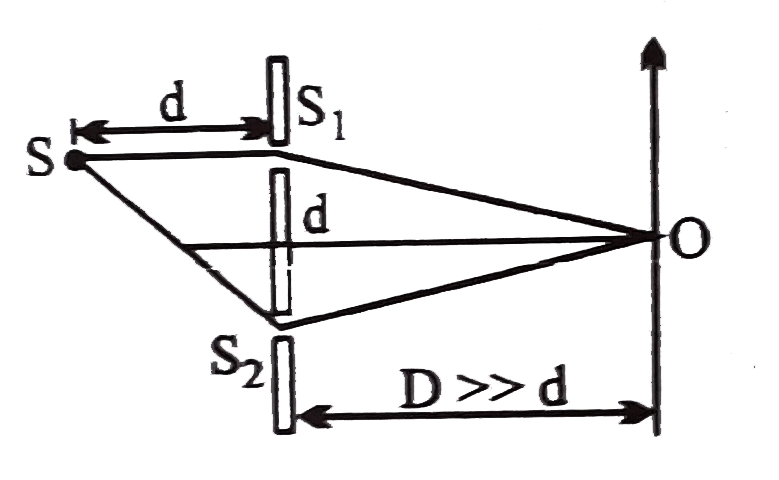 AThe thickness of sheet is 2(√2−1)d infornt of S1BThe thickness of sheet is (√2−1)d infornt of S2CThe thickness of sheet is 2√2d infornt of S1DThe thickness of sheet is (2√2−1)d infornt of S1
AThe thickness of sheet is 2(√2−1)d infornt of S1BThe thickness of sheet is (√2−1)d infornt of S2CThe thickness of sheet is 2√2d infornt of S1DThe thickness of sheet is (2√2−1)d infornt of S1
Two transparent sheets of thickness t1 and t2 and refractive indexes μ1 and μ2 are placed infront of the slits in YDSE setup as shown in figure-6.47. If D is the distance of the screen from the slits, then find the distance of zero order maxima from the centre of the screen. What is the condition that zero order maxima is formed at the centre O?

[D[(μ1−1)t1−(μ2−1)t2]d,(μ2−1)t2]
View SolutionIn YDSE, let A and B be two slits. Films of thickness tA and tB and refractive μA and μB are placed in front of A and B, respectively. If μAtA=μAtB, then the central maxima will
View SolutionA stationary swimmer S, inside a liquid of refractive index μ1, is at a distance d from a fixed point P inside the liquid. A rectangular block of width t and refractive index μ2(μ2<μ1) is now placed between S and P.S will observer P to be at a distance
View SolutionA beaker is filled with two immiscible transparent liquids of refractive indices μ1 and μ2 having thickness of layers d1 and d2 respectively. The apparent depth of the bottom of the beaker is
View SolutionIn the YDSE shown the two slits are covered with thin sheets having thickness t&2t and refractive index 2μand μ .Find the position (y) of central maxima.

View Solution

