एक श्वेत प्रकाश स्रोत द्वारा प्रकाशित दो रेखाछिद्र S1 और S2 एक श्वेत केंद्रीय उच्चिष्ठ बनाते हैं।
1. 25 अपवर्तनांक और t1 मोटाई की एक पारदर्शी शीट को S1 के सामने रखा गया है। 1.50 अपवर्तनांक और t2 मोटाई की एक अन्य पारदर्शी शीट को S2 के सामने रखा गया है। यदि केंद्रीय उच्चिष्ठ प्रभावित नहीं होता है, तो अनुपात t1:t2 होगा:
1:2
2:1
1:4
4:1
The correct Answer is:B
चूंकि, केंद्रीय उच्चिष्ठ में कोई विस्थापन नहीं होता है। अत: दो शीटों द्वारा प्रस्तुत पथांतर बराबर है:
अर्थात्,
(μ1−1)t1=(μ2−1)t2
जहां, μ1 और μ2 अपवर्तनांक हैं
अर्थात, t1t2=(μ2−1)(μ1−1)=(1.5−1)(1.25−1)=0.50.25=2
Topper's Solved these Questions
Similar Questions
यदि छड़ चुंबक पर कार्य करने वाले चुंबकीय बल आघूर्ण τ1,τ2,τ3 और τ4 हैं, जब इसे चुंबकीय क्षेत्र की दिशा के साथ क्रमश: 30∘,60∘,90∘ और 135∘ के कोणों पर रखा जाता है, तो निम्नलिखित में से कौन सा सही है?
View Solution1.5×1013 Hz की आवृत्ति वाले फोटॉन का संवेग क्या है?
View SolutionIn an A.P. if S1=T1+T2+T3+.....+Tn(nodd).S2=T2+T4+T6+.........+Tn−1 , then find the value of S1/S2 in terms of n.
View SolutionIn an A.P.if S_(1)=T_(1)+T_(2)+T3+...+T_(n) (n odd S_(2)=T_(1)+T_(3)+T_(5)+...+T_(n) then (S_(1))/(S_(2))=
View SolutionLet s1,s2,s3,..andt1,t2,t3..... are two arithmetic sequences such that s1=t1≠0,s2=2t2 and 10∑i=1s1=15∑i=1t1 .Then the value of s2−s1t2−t1 is
View SolutionSuppose a series of n terms given by Sn=t1+t2+t3+. . . .+tn
then Sn−1=t1+t2+t3+. . . .+tn−1,n≥1 subtracting we get Sn−Sn−1=tn,n≥2 surther if we put n=1 is the first sum then S1=t1 thus w can write tn=Sn−Sn−1,n≥2 and t1=S1
Q. The sum of n terms of a series is a.2n−b. where a and b are constant then the series is
View SolutionSuppose a series of n terms given by Sn=t1+t2+t3+. . ..+tn
then Sn−1=t1+t2+t3+ . . . +tn−1,n≥1 subtracting we get Sn−Sn−1=tn,n≥2 surther if we put n=1 is the first sum then S1=t1 thus w can write tn=Sn−Sn−1,n≥2 and t1=S1
Q. if the sum of n terms of a series a.2n−b then the sum ∞∑r=11tr is
View SolutionLet s1,s2,s3....andt1,t2,t3.... are two arithmetic sequences such that s1=t1≠0,s2=2t2and10∑i=1si=15∑i=1ti. Then the value of s2−s1t2−t1 is
View Solutionसिद्ध कीजिये की बिंदु (1,−2),(3,6),(5,10) और (3,2) एक समांतर चतुर्भुज के शीर्ष है ।
View Solutionतथाकथित त्रिभुजीय संख्याएँ Tn लीजिये :
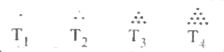
बिन्दुओ का विन्यास इस प्रकार किया गया है की इनसे एक त्रिभुज बनता है ।
यहाँ T1=1,T2=3,T3=6,T4=10 आदि आदि। क्या आप अनुमान लगा सकते है की T5 क्या है।
T6 के बारे में आप क्या कह सकते है ?
Tn के बारे में आप क्या कह सकते है ?
T8 का एक कंजेक्चर दीजिये।
View Solution(1) किसी A.P. के प्रथम 10 पदों का योगफल ज्ञात कीजिए यदि T1=−14 और T5=20.
(ii) किसी A.P. का तीसरा पद 14 और 8वाँ पद 34 है।Sn और S30 ज्ञात कीजिए।
View Solutionएक पुस्तक की मोटाई 2 सेमी है और इसमें 800 पृष्ठ है। एक पृष्ठ की मोटाई मानक रूप में ज्ञात कीजिए।
View SolutionSuppose a series of n terms given by Sn=t1+t2+t3+. . . .+tn
then Sn−1=t1+t2+t3+. . . .+tn−1,n≥1 subtracting we get Sn−Sn−1=tn,n≥2 surther if we put n=1 is the first sum then S1=t1 thus w can write tn=Sn−Sn−1,n≥2 and t1=S1
Q. The sum of n terms of a series is a.2n−b. where a and b are constant then the series is
View SolutionSuppose a series of n terms given by Sn=t1+t2+t3+. . ..+tn
then Sn−1=t1+t2+t3+ . . . +tn−1,n≥1 subtracting we get Sn−Sn−1=tn,n≥2 surther if we put n=1 is the first sum then S1=t1 thus w can write tn=Sn−Sn−1,n≥2 and t1=S1
Q. if the sum of n terms of a series a.2n−b then the sum ∞∑r=11tr is
View SolutionLet s1,s2,s3....andt1,t2,t3.... are two arithmetic sequences such that s1=t1≠0,s2=2t2and10∑i=1si=15∑i=1ti. Then the value of s2−s1t2−t1 is
View SolutionIn an A.P. if S_(1) = T_(1) + T_(2) + T_(3) +…+ T_(n) (n odd) S_(2) = T_(1) + T_(3) + T_(5) + …+ T_(n) , then S_(1)//S_(2) =
View Solution
