The dimensions of $' k'$ in the relation $V = k$ avt (where $V$ is the volume of a liquid passing through any point in time $t,' a'$ is area of cross section, $v$ is the velocity of the liquid) is

A

$[M^{1} L^{2} T^{- 1}]$

B

$[M^{1} L^{1} T^{- 1}]$

C

$[M^{0} L^{0} T^{- 1}]$

D

$[M^{0} L^{0} T^{0}]$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Substitude $D . F$ of quantities

|

Updated on:21/07/2023

Class 11 PHYSICS DIMENSION AND MEASUREMENT

Topper's Solved these Questions

BOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - LEVEL-II (C.W)
28videos
UNITS AND MEASUREMENTS
BOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - LEVEL-III
21videos
UNITS AND MEASUREMENTS
BOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - C.U.Q
183videos
UNITS AND MEASUREMENTS
BOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - LEVEL-II(C.W)
27videos
TRANSMISSION OF HEAT
BOOK - NARAYNACHAPTER - VECTORSEXERCISE - LEVEL-II (H.W)
14videos
VECTORS

Similar Questions

Knowledge Check

Question 1 - Select One
The dimensions of $γ$ in the relation $v = \sqrt{\frac{γ p}{ρ}}$ (where $v$ is velocity, $p$ is pressure , $ρ$ is density)
ADimensionless
B $[L T^{- 1}]$
C $[M L^{- 1} T^{- 2}]$
D $[M L^{- 3}]$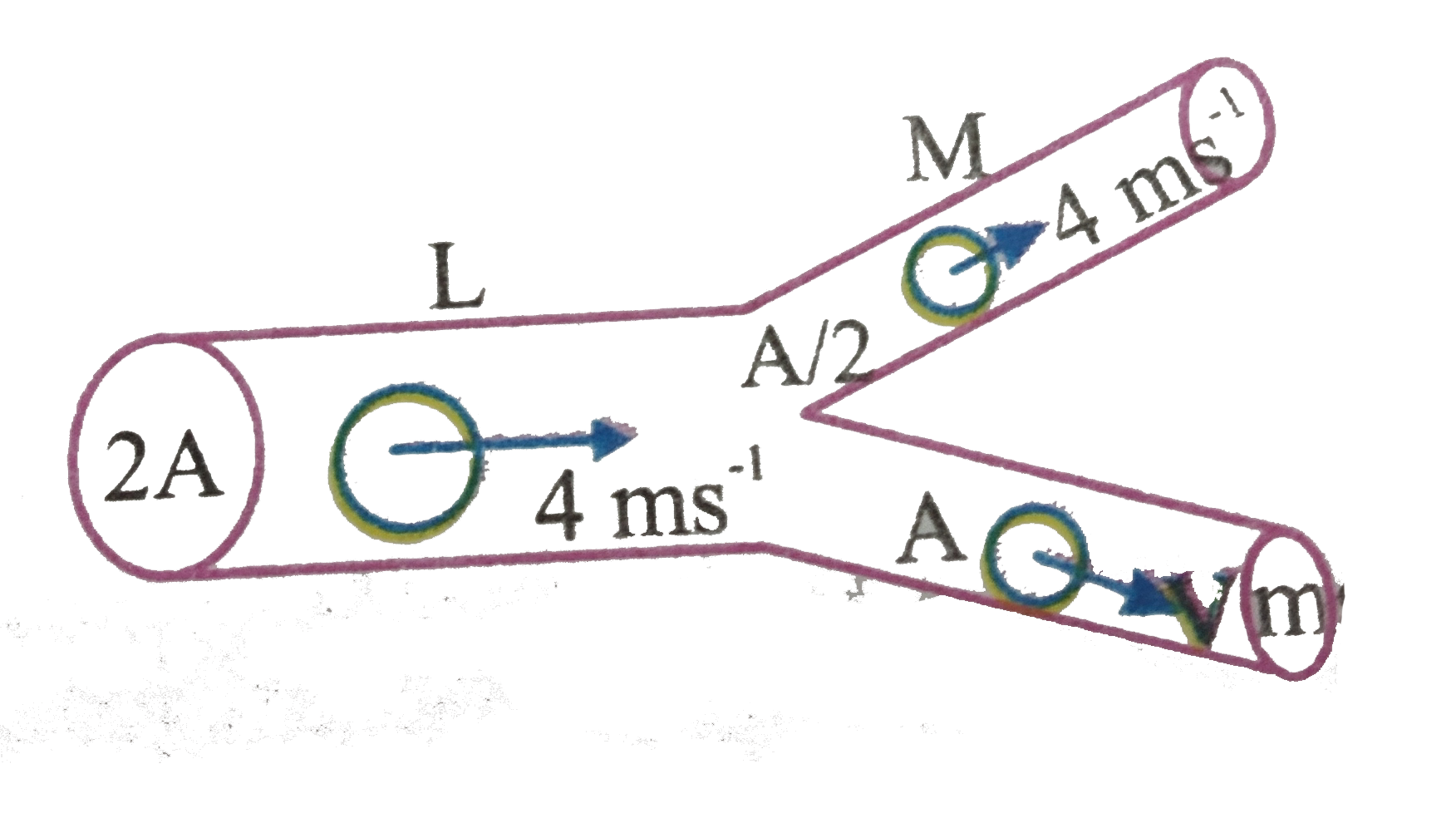
Question 2 - Select One

An incompressible liquid flows through a horizontal tube LMN as shown in the figure. Then the velocity $V$ of the liquid throught he tube N is:
A $1 m s^{- 1}$
B $2 m s^{- 1}$
C $4.5 m s^{- 1}$
D $6 m s^{- 1}$
Question 3 - Select One or More
A liquid of density $ρ$ comes out with a velocity v from a horizontal tube of area of cross-section A. The reaction force exerted by the liquid on the tube is F :
A $F \propto v$
B $F \propto v^{2}$
C $F \propto A$
D $F \propto ρ$

NARAYNA-UNITS AND MEASUREMENTS-LEVEL-I (C.W)

Home
Ask Doubt
Profile