The dimensionla formula for the product of two physical quantities P and Q is [ML2T−2]. The dimensional formula of PQ is [MT−2]. Then P and Q respectively are
Force and velocity
Momentum and displacement
Force and displacement
Work and velocity
The correct Answer is:C
To find the dimensional formulas for the physical quantities P and Q, we start with the information given in the problem:
1. The dimensional formula for the product of P and Q is:
(P⋅Q)=(ML2T−2)
2. The dimensional formula for the ratio PQ is:
(PQ)=(MT−2)
Step 1: Set up the equations
From the information provided, we can express the dimensional formulas of P and Q as follows:
- Let the dimensional formula of P be (MaLbTc).
- Let the dimensional formula of Q be (MdLeTf).
Step 2: Write the equations based on the product and ratio
From the product P⋅Q:
(MaLbTc)⋅(MdLeTf)=(Ma+dLb+eTc+f)=(ML2T−2)
This gives us the following equations:
1. a+d=1 (1)
2. b+e=2 (2)
3. c+f=−2 (3)
From the ratio PQ:
(MaLbTc)(MdLeTf)=(Ma−dLb−eTc−f)=(MT−2)
This gives us the following equations:
4. a−d=1 (4)
5. b−e=0 (5)
6. c−f=−2 (6)
Step 3: Solve the equations
Now we can solve these equations step by step.
From equations (1) and (4):
1. From (1): a+d=1
2. From (4): a−d=1
Adding these two equations:
(a+d)+(a−d)=1+1⟹2a=2⟹a=1
Substituting a=1 into equation (1):
1+d=1⟹d=0
From equations (2) and (5):
1. From (2): b+e=2
2. From (5): b−e=0
Adding these two equations:
(b+e)+(b−e)=2+0⟹2b=2⟹b=1
Substituting b=1 into equation (2):
1+e=2⟹e=1
From equations (3) and (6):
1. From (3): c+f=−2
2. From (6): c−f=−2
Adding these two equations:
(c+f)+(c−f)=−2−2⟹2c=−4⟹c=−2
Substituting c=−2 into equation (3):
−2+f=−2⟹f=0
Step 4: Write the final dimensional formulas
Now we have:
- P:(M1L1T−2)
- Q:(M0L1T0)
Thus, the dimensional formulas for P and Q are:
P=(ML1T−2),Q=(L1)
Final Answer:
- P has the dimensional formula (ML1T−2)
- Q has the dimensional formula (L1)
(P⋅Q)=(ML2T−2)
(PQ)=(MT−2)
From the information provided, we can express the dimensional formulas of P and Q as follows:
- Let the dimensional formula of P be (MaLbTc).
- Let the dimensional formula of Q be (MdLeTf).
From the product P⋅Q:
(MaLbTc)⋅(MdLeTf)=(Ma+dLb+eTc+f)=(ML2T−2)
This gives us the following equations:
1. a+d=1 (1)
2. b+e=2 (2)
3. c+f=−2 (3)
(MaLbTc)(MdLeTf)=(Ma−dLb−eTc−f)=(MT−2)
This gives us the following equations:
4. a−d=1 (4)
5. b−e=0 (5)
6. c−f=−2 (6)
Now we can solve these equations step by step.
1. From (1): a+d=1
2. From (4): a−d=1
(a+d)+(a−d)=1+1⟹2a=2⟹a=1
Substituting a=1 into equation (1):
1+d=1⟹d=0
1. From (2): b+e=2
2. From (5): b−e=0
(b+e)+(b−e)=2+0⟹2b=2⟹b=1
Substituting b=1 into equation (2):
1+e=2⟹e=1
1. From (3): c+f=−2
2. From (6): c−f=−2
(c+f)+(c−f)=−2−2⟹2c=−4⟹c=−2
Substituting c=−2 into equation (3):
−2+f=−2⟹f=0
Now we have:
- P:(M1L1T−2)
- Q:(M0L1T0)
P=(ML1T−2),Q=(L1)
- P has the dimensional formula (ML1T−2)
- Q has the dimensional formula (L1)
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:LEVEL-II (C.W)
Explore 28 Videos
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:LEVEL-III
Explore 21 Videos
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:C.U.Q
Explore 183 Videos
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL-II(C.W)
Explore 27 Videos
- VECTORSBook:NARAYNAChapter:VECTORSExercise:LEVEL-II (H.W)
Explore 14 Videos
Similar Questions
Knowledge Check
The demensional formula for the product of two physical quantites P and Q is [L2T−2] the dimensional formula of P/Q is [T2] the P and Q respectively are......
Adistance and velocityBdistance and accelerationCdisplacement and velocityDdisplacement and forceThe dimensional formula of product and quotient of two physical quantities A and B are given by [AB]=[ML2T−2],[AB]=[MT−2]. The quantities A and B respectively are
Aforce and velocityBForce and displacementCMomentum and displacementDWork and velocityIf the dimensional formula for the physical quantity is [M1L2T−2] then the physical quantity is ______ .
AtorqueBimpulseCforceDforce per unit area
Dimensional formula ML−1T2 does not represent the physical quantity
View Solution
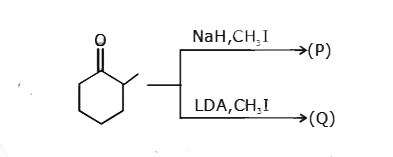
The products P & Q are respectively
View SolutionThe dimensional formula [ML−1T−2] is for the quantity
View SolutionThe SI unit of a physical quantity having the dimensional formula of [ML^(0)T^(-2) A^(-1)]
View SolutionTwo physical quantities are represented by P and Q. The dimensions of their product is [M2L−4T−4I−1] and dimensions of their ratio is [I−1]. Then P and Q respectively are
View Solution