In the figure, M is the midpoint of QR. ∠PRQ=90∘. Prove that PQ2=4PM2−3PR2
The correct Answer is:∴PQ2=4PM2−3PR2.
Step by step video, text & image solution for In the figure, M is the midpoint of QR. /_PRQ=90^(@). Prove that PQ^(2)=4PM^(2)-3PR^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREM Book:TARGET PUBLICATIONChapter:PYTHAGORAS THEOREM Exercise:Try this
Explore 1 Video
- PYTHAGORAS THEOREM Book:TARGET PUBLICATIONChapter:PYTHAGORAS THEOREM Exercise:Practice Set 2.2
Explore 1 Video
- PYTHAGORAS THEOREM Book:TARGET PUBLICATIONChapter:PYTHAGORAS THEOREM Exercise:Chapter Assessment
Explore 16 Videos
- PROBABILITYBook:TARGET PUBLICATIONChapter:PROBABILITYExercise:Try This
Explore 1 Video
- QUADRATIC EQUATIONSBook:TARGET PUBLICATIONChapter:QUADRATIC EQUATIONSExercise:Additional problems for Practice : Based on Practice set 2.6
Explore 30 Videos
Similar Questions
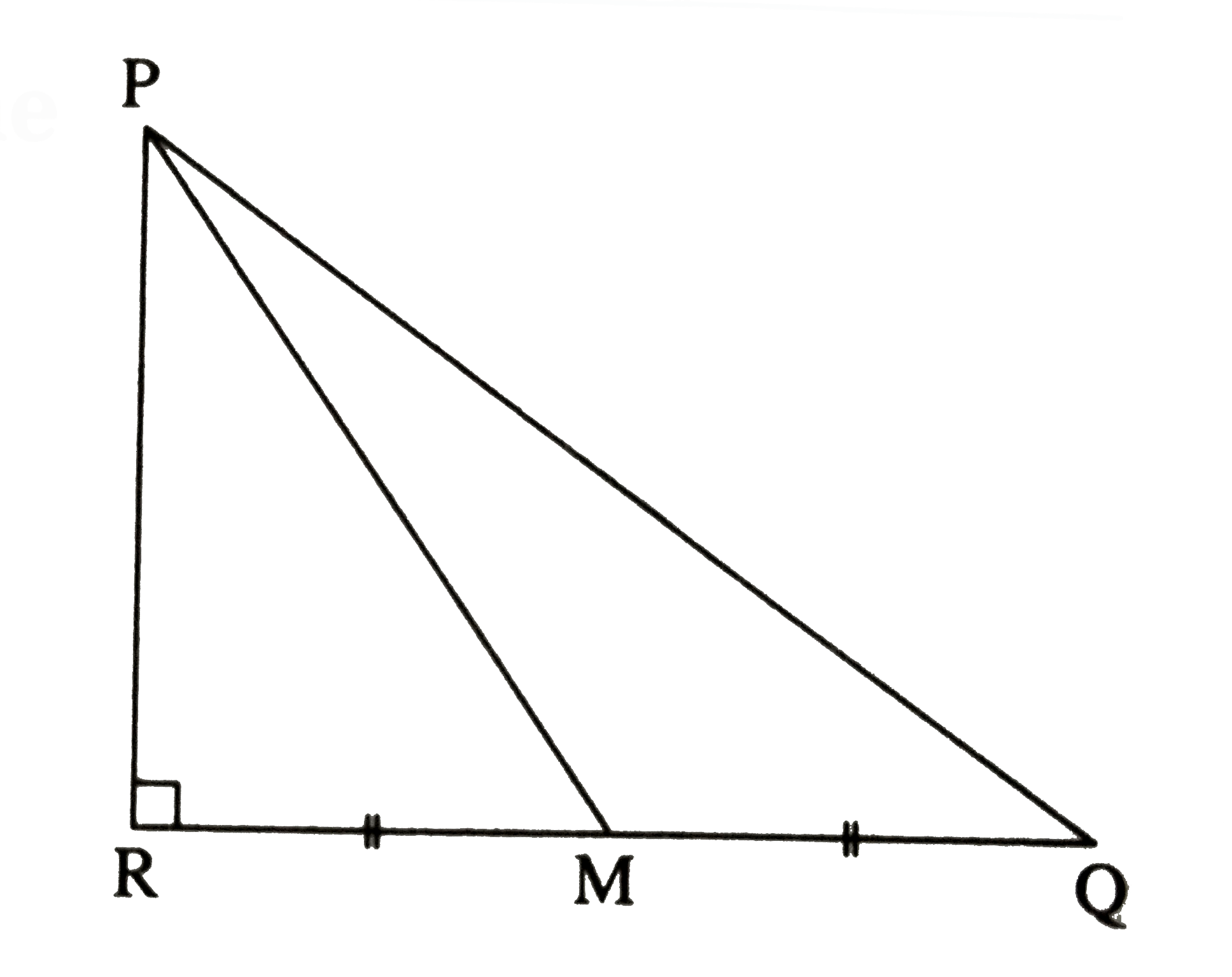
In the given figure, M is the midpoint of QR. ∠PQR=90∘.
Prove that, PQ2=4PM2−3PR2.
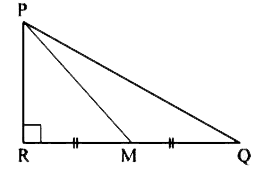
View SolutionIn the figure , M is the midpoint of QR .
∠PRQ=90∘.
Prove that ,
PQ2=4PM2−3PR2 .
View SolutionIn adjoining figure, seg PS is the median of ΔPQRadnPT⊥QR. Prove that
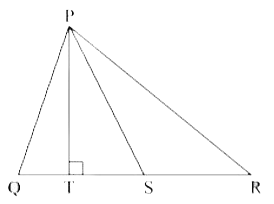
(1) PR2=PS2+QR×ST+(OR2)2
(2) PQ2=PS2+QR×ST+(QR2)2
View SolutionIf S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.
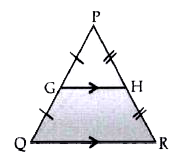
View SolutionIn the given figure G is the mid-point of the side PQ of ΔPQR and GH || QR .Prove that H is the mid -point of the side PR of the triangle PQR .
View SolutionIn the given figure, seg PM is a median of ΔPQR.PM=9andPQ2+PR2=290, then find QR.

View Solution1. In the figure △PQR is an equilateral triangle, the point N is on ray QR such that QR=RN. Prove that PN2=3PR2
View SolutionIn the figure given below, ΔPQR is right-angled at Q and the points S and T trisect the side QR. Prove that 8PT2=3PR2+5PS2
View SolutionIn the figure in ∠PQR=∠PRQ then prove that ∠PQS=∠PRT
View SolutionIn PQR, QM⊥PR and PR2−PQ2=QR2 . Prove that QM2=PM×MR
View Solution

