In the figure, ∠QPR=90∘, seg PM⊥ seg QR and Q−M−R, PM=10. QM=8, find QR.
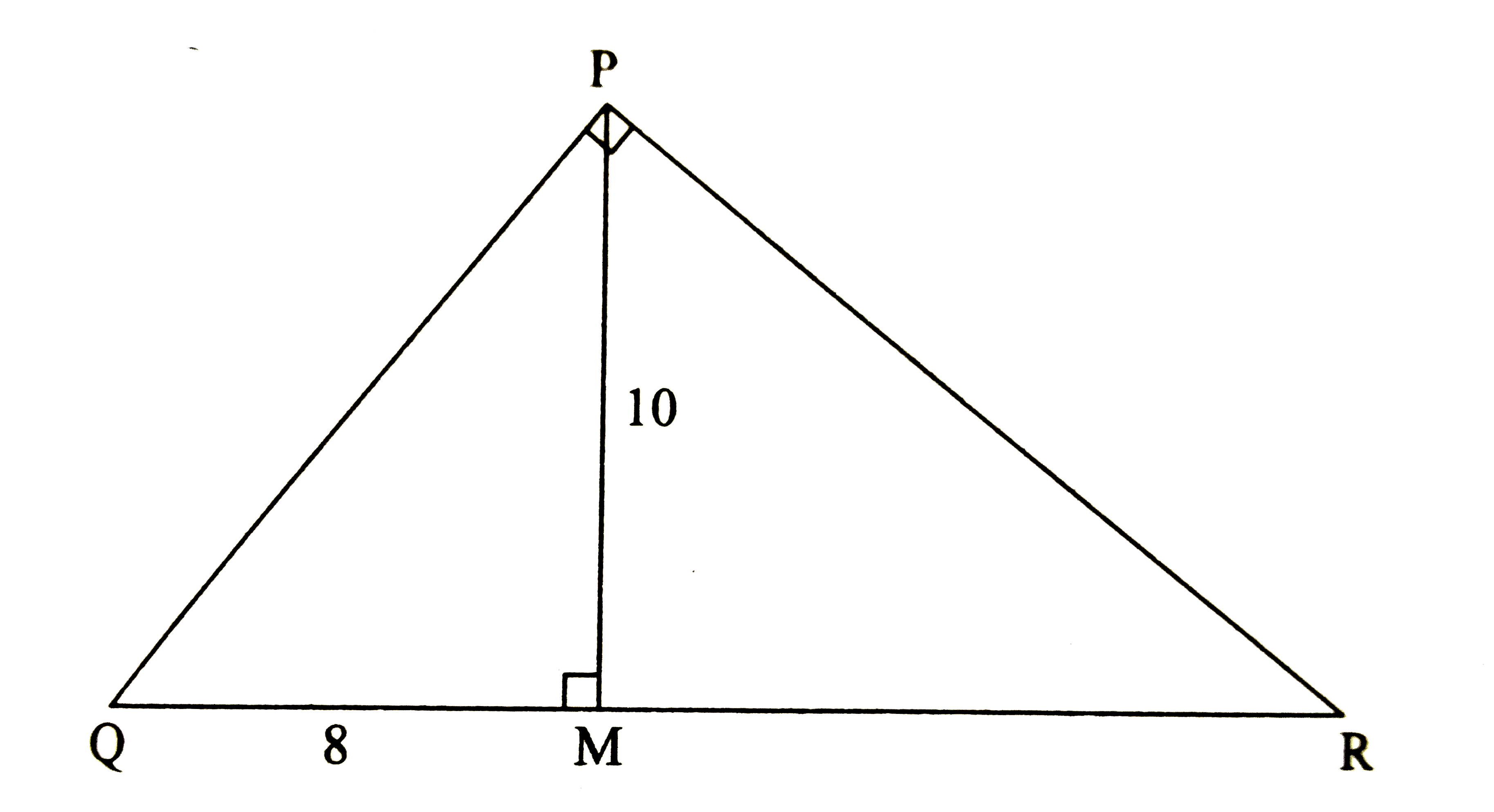
The correct Answer is:∴QR=20.5 units
Step by step video, text & image solution for In the figure, /_QPR=90^(@), seg PM bot seg QR and Q-M-R, PM=10. QM=8, find QR. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREM BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Try this
1 Videos
- PYTHAGORAS THEOREM BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Practice Set 2.2
1 Videos
- PYTHAGORAS THEOREM BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Chapter Assessment
16 Videos
- PROBABILITYBOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Try This
1 Videos
- QUADRATIC EQUATIONSBOOK - TARGET PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - Additional problems for Practice : Based on Practice set 2.6
30 Videos
Similar Questions
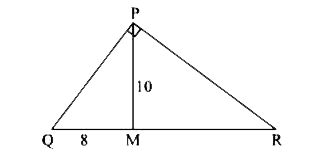
In the adjoining figure.
∠QPR=90∘,
seg PM⊥segQRandQ−M−R,PM=10,QM=8, find QR.
View SolutionIn the given figure, ∠PQR=90∘, seg QN⊥segPR,PN=9,NR=16.Find QN.
View SolutionIn ΔPQR,∠PQR=90∘,segQS⊥segPR, then find x,y,z.
View SolutionIn ΔPQR,∠PQR=90∘,
seg QS⊥ seg PR then find x,y,z.
View SolutionIn ΔPQR,∠Q=90∘, seg RS⊥ side PR. If PQ=16,QR=30. Find QS.
View SolutionIn the figure, ∠DFE=90∘, seg FG⊥ side DE, DG=8, FG=12 then complete the following activity to find the length of seg DE.
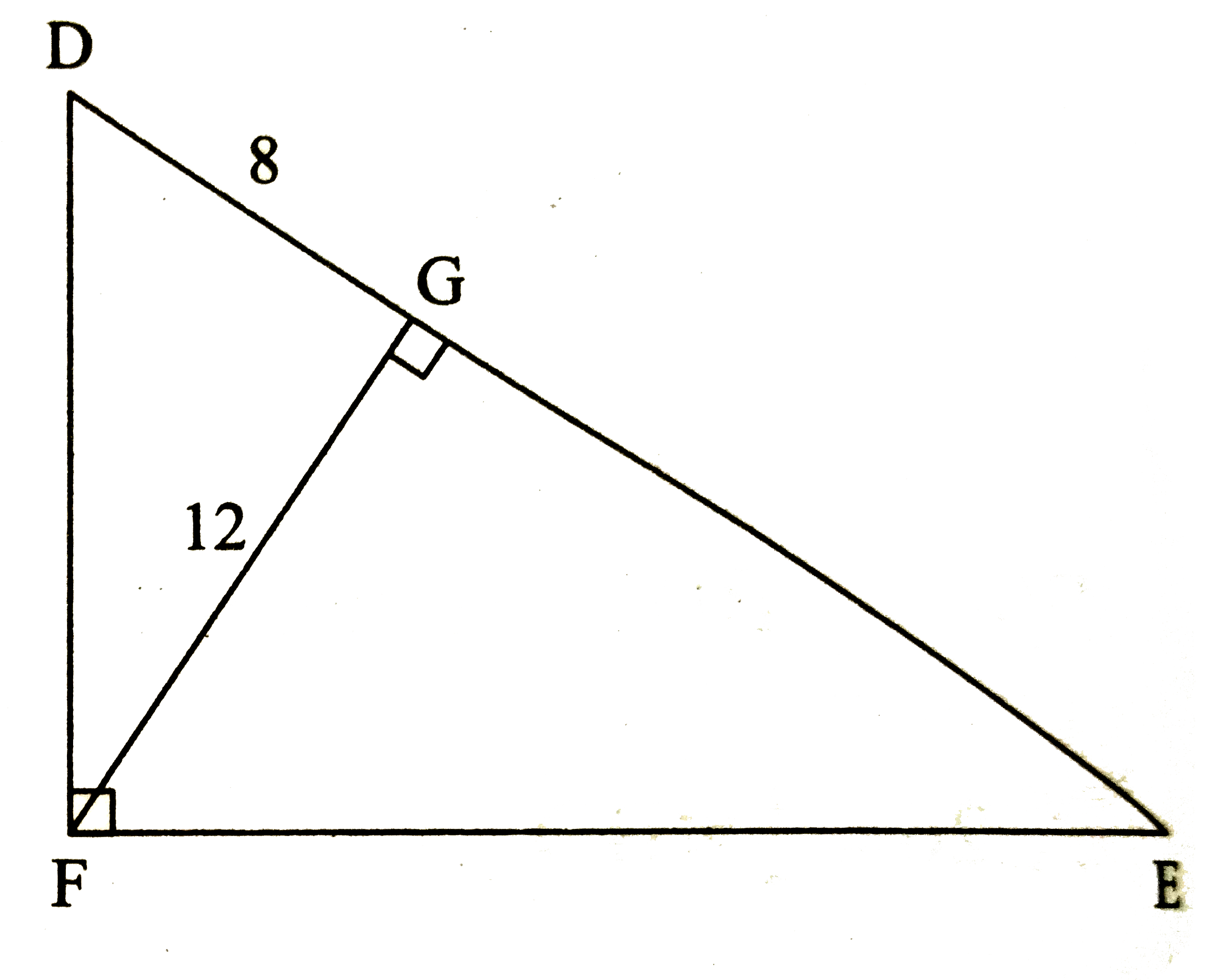
In ΔDFE, ∠DFE=90∘,
seg FG⊥ hypotenuse DE
∴ by theorem of geometric mean,
FG2=□×EG
∴122=□×EG
EG=12×12□
∴EG=□
DE=DG+GE=8+□=□
View SolutionIn the figure , ∠PQR=32∘ seg SN ⊥ray QP and seg SM ⊥ ray QR . Find ∠ PQS . state the reason for your answer.
View Solution
In the figure ,segPQ || seg SR and PQ =SR =5 cm . If QR =10 cm , then find PS . Justify your answer.
View SolutionIn the figure, ∠LMN=∠LKN=90∘
seg MK⊥ seg LN.
Complete the following activity to prove R is the midpoint of seg MK.
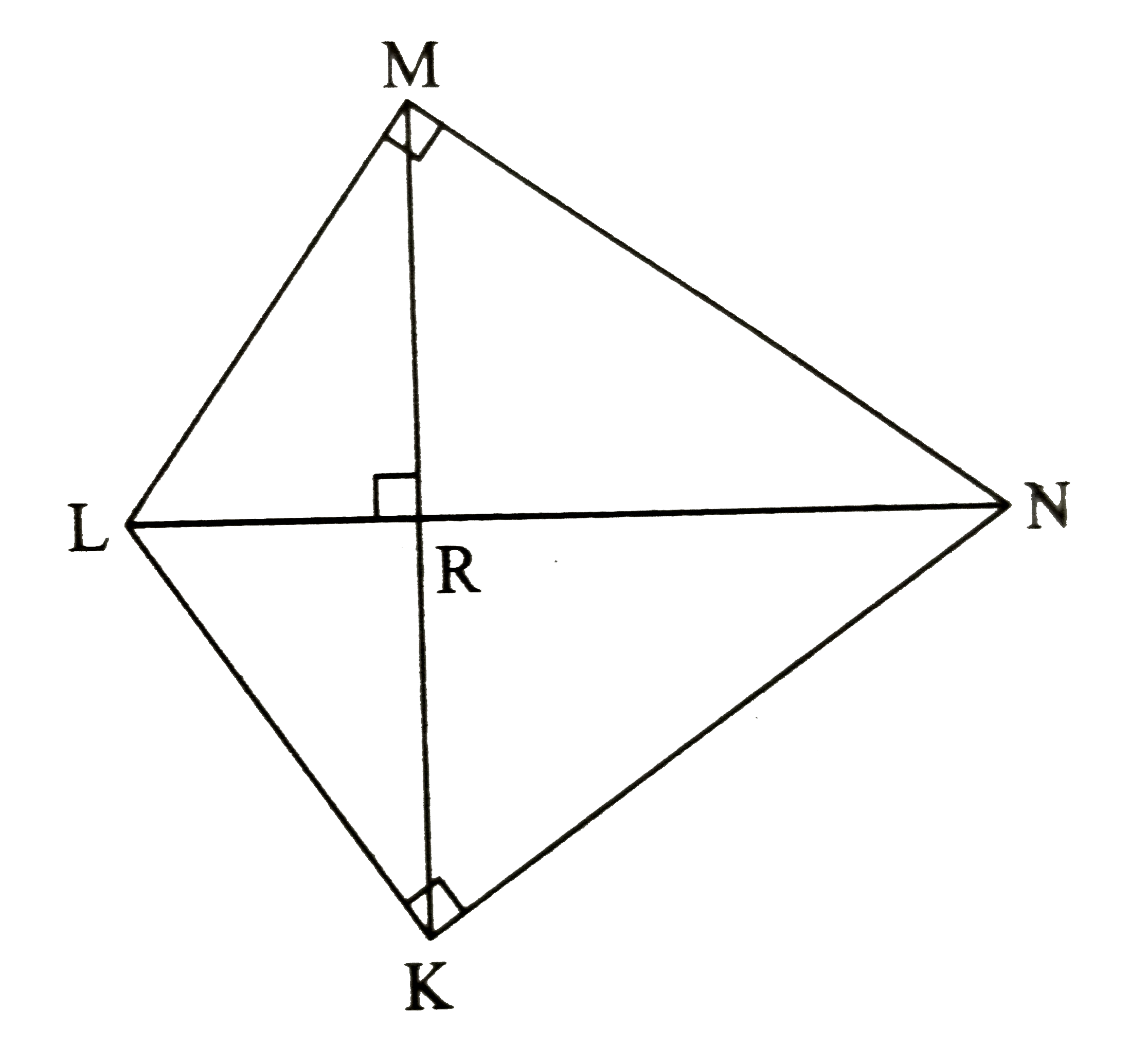
Proof: In ΔLMN, ∠LMN=90∘
seg MR⊥ hypotenuse LN
∴ by property of geometric mean,
MR2=□×RN
In ΔLKN, ∠LKN=90∘
seg KR⊥ hypotenuse LN
∴ by property of geometric mean,
KR2=LR×□
From (1) and (2), we get
MR2=□∴MR=□.
∴R is the midpoint of seg MK.
View SolutionIn ΔABC,∠A=90∘, seg BP⊥ side AC.AP=2,PC=8. Find BP.
View Solution
