O is the origin and A is a fixed point on the circle of radius 'a' with centre O.The vector →OA is denoted by →a . A variable point P lie on the tangent at Aand→OP−→r. Show that →a→r=a2.Hence if P(x,y)andA(x1,y1), deduce the equation of tangent at A to this circle.
The correct Answer is:×1+2yy1=a
Step by step video, text & image solution for O is the origin and A is a fixed point on the circle of radius 'a' with centre O.The vector vec O A is denoted by vec a . A variable point P lie on the tangent at A and vec OP-vec r. Show that vec a vec r=a^2.Hence if P(x, y) and A(x_1, y_1), deduce the equation of tangent at A to this circle. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 52 Videos
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise (Single Integer Answer Type Questions)
Explore 16 Videos
- PROBABILITYBook:ARIHANT MATHSChapter:PROBABILITYExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 55 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 21 Videos
Similar Questions
O is the origin and A is a fixed point on the circle of radius 'a' with centre O.The vector →OA is denoted by →a . A variable point P lie on the tangent at Aand→OP−→r. Show that →a→r=a2.Hence if P(x,y)andA(x1,y1), deduce the equation of tangent at A to this circle.
View SolutionIf P,Q and R are three collinear points such that →PQ=→a and →QR = →b. Find the vector →PR .
View SolutionIn a triangle ΔOAC, if B is the mid point of side AC and −−→OA=→a, −−→OB=→b, then what is −−→OC?
View SolutionThe three vectors →A,→Band→C are repesented in magnitude and direction by −−−−−−−→OP,−−→OQ, show that (S) is the mid point of (PQ).
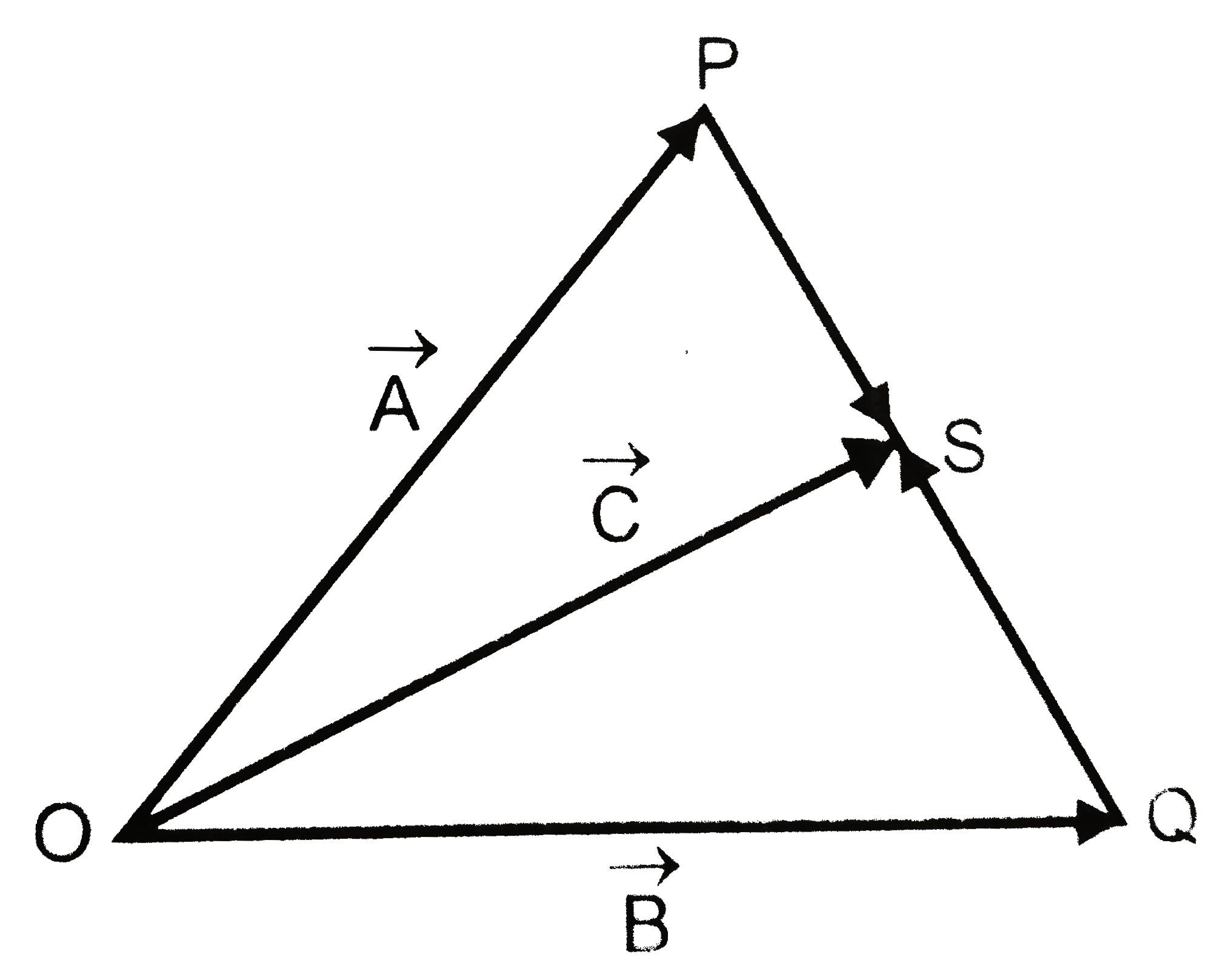 .
.
View SolutionIf →a, →b, →c are position vectors o the point A, B, and C respectively, write the value of →AB+→BC+→AC.
View SolutionVectors drawn the origin O to the points A,BandC are respectively →a,→band→4a−→3b. find →ACand→BC.
View SolutionGiven a regular hexagon ABCDEF with centre O, show that →OB−→OA=→OC−→OD
View Solution→a,→b,→c are three non-zero vectors. If ⊕ be defined as →x⊕→y=→x+→y+→x×→y and
View SolutionP(→p)andQ(→q) are the position vectors of two fixed points and R(→r) is the position vectorvariable point. If R moves such that (→r−→p)×(→r−→q)=0 then the locus of R is
View SolutionFor three vectors →p,→q and →r if →r=3→p+4→q and 2→r=→p−3→q then
View Solution

