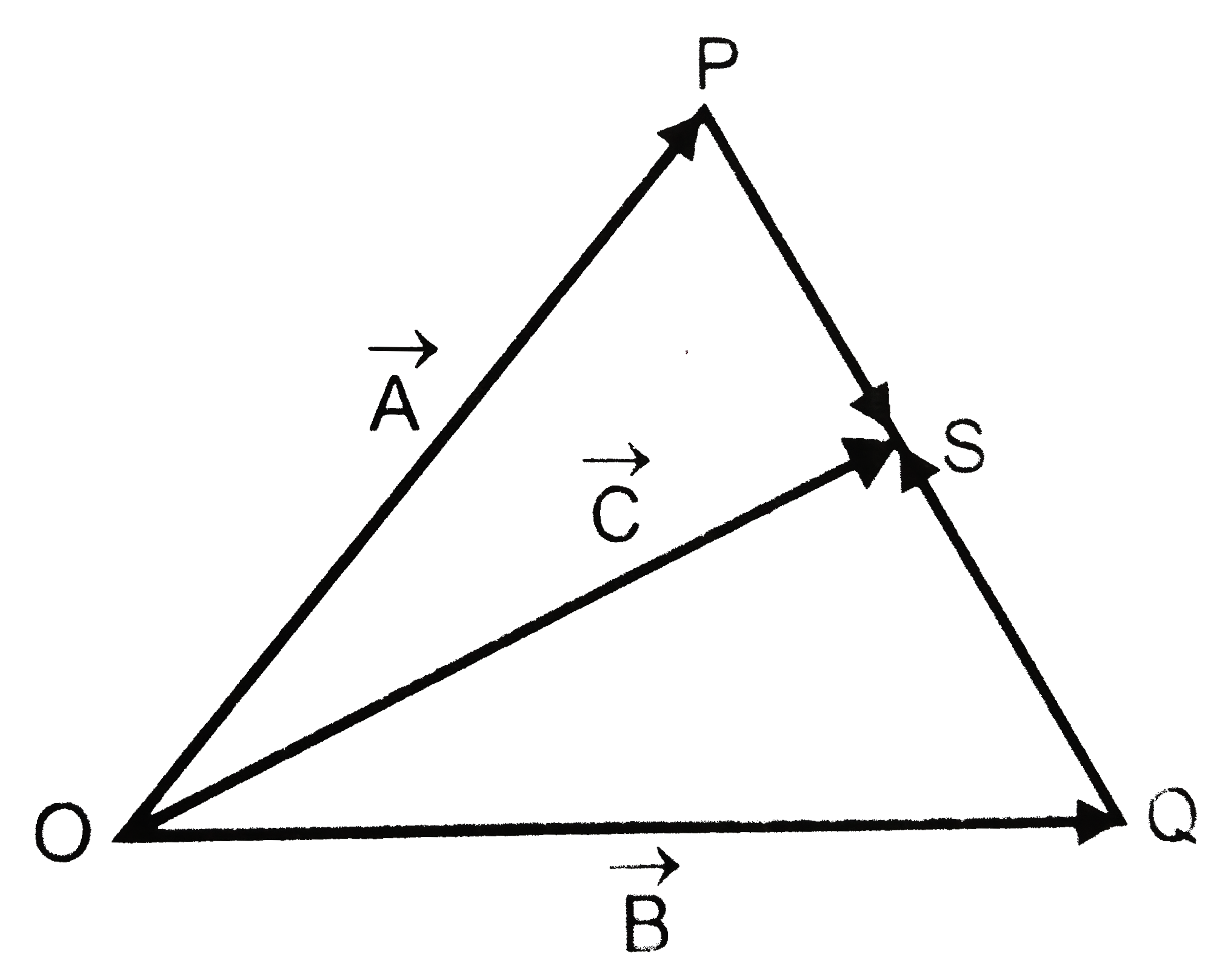
The three vectors $\to A, \to B and \to C$ are repesented in magnitude and direction by $- ------ \to O P, - - \to O Q,$ show that (S) is the mid point of (PQ).
.

Video Solution

Text Solution

Verified by Experts

In $Δ O P S$ , by vectors addition,
$- - \to O S = - - \to O P + - - \to O S$ ….(i)
Similarly, in $Δ O Q S$ , we have
$- - \to O S = - - \to O Q + - - \to Q S$ …(ii)
Adding (i) and (ii), we have
$2 - - \to O S = - - \to O P + - - \to O Q + - \to P S + - - \to Q S$
or $\to C = \to A + \to B + - \to P S + - - \to Q S$
or $(2 \to C - \to A - \to B) = - \to P S + - - \to Q S$
or $0 = - \to P S + - - \to Q S ⟨ . 2 \to C = \to A + \to B)$
or $- \to P S = - - - \to Q S$ .
So, (S) is the mid point of (PQ)

|

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Three vector $\to A$ , $\to B$ , $\to C$ satisfy the relation $\to A \cdot \to B = 0$ and $\to A . \to C = 0$ . The vector $\to A$ is parallel to
A $\to B$
B $\to C$
C $\to B . \to C$
D $\to B \times \to C$

PRADEEP-KINEMATICS-3 Con ceptual Problems

Home
Ask Doubt
Profile