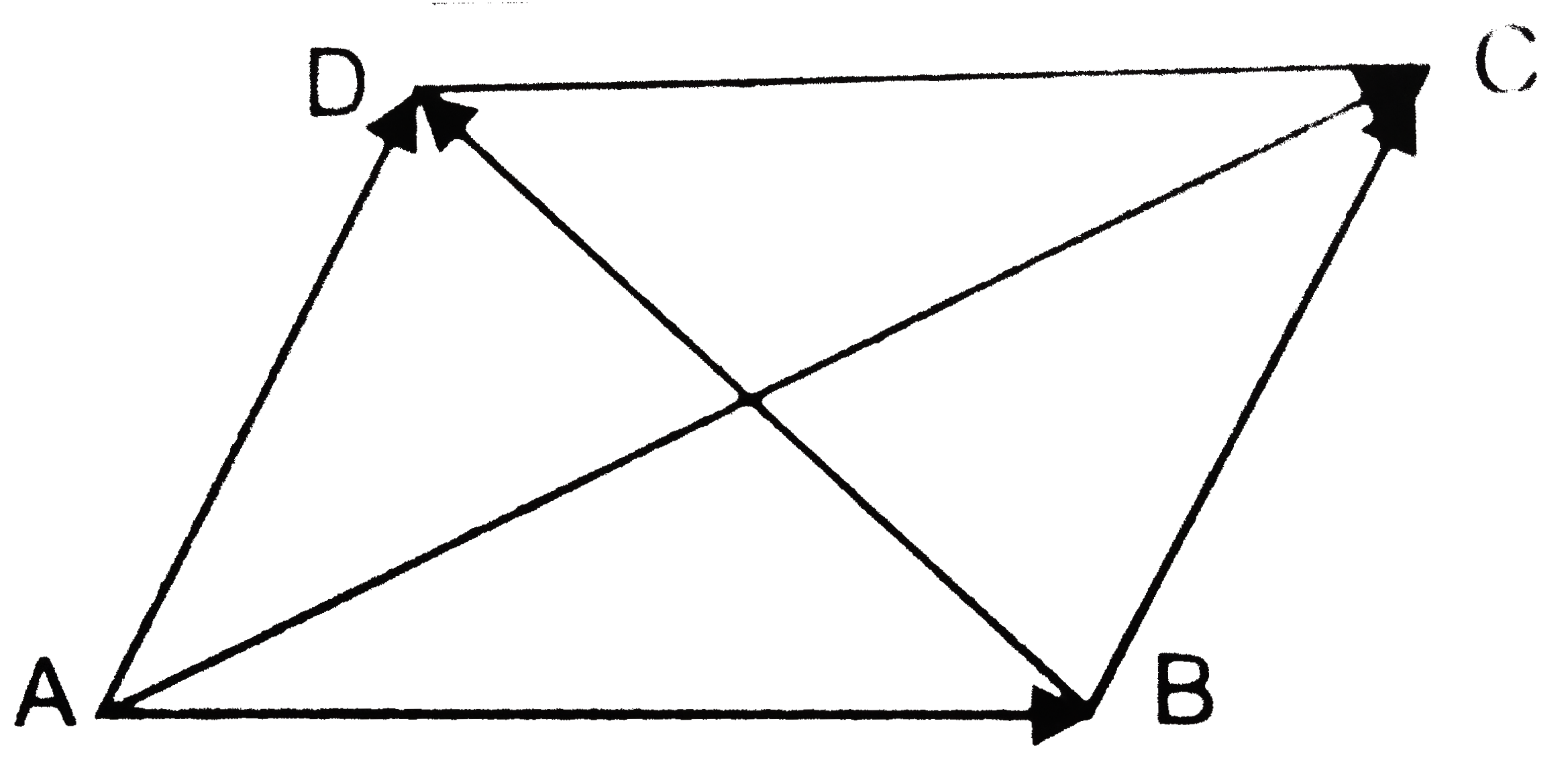
ABCD is a parallelogram Fig. 2 (c ) .64. ACand(BD)areitsdiagonals.Showtˆ<br> (a) vec (AC) +vec (BD) =2 vec (BC)<br>(b)vec (AC) - vec (BD) =2 vec (AB)
 .
.
Video Solution
Text Solution
(a) Refer to Fig. 2 (c ). 64, using trianle law of v ec tors, we have,
−−→AC+−−→BD=(−−→AB+−−→BC+−−→BC+−−→CD
=−−→AB+2−−→BC+−−→CD
=−−→AB=2−−→BC−−−→AB
⟨.Vec(CD)=−−−→AB
or −−→AC+−−→BD=2−−→BC
(b) −−→AC−−−→BD=−−→AB+−−→BC−−−→BC+→AB)
=−−→AB−−−→CD
−−→AC−−−→BC=(AB)−(−AB)=2VEC(AB).
|
Topper's Solved these Questions
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:4 Conceptual Problems
Explore 1 Video
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:4 Con ceptual Problems
Explore 22 Videos
- KINEMATICSBook:PRADEEPChapter:KINEMATICSExercise:2 Con ceptual Problems
Explore 15 Videos
- GRAVIATIONBook:PRADEEPChapter:GRAVIATIONExercise:Assertion-Reason Type Questions
Explore 19 Videos
- LAWS OF MOTIONBook:PRADEEPChapter:LAWS OF MOTIONExercise:Assertion- Reason Type Questions
Explore 17 Videos
Similar Questions
Knowledge Check
ABCD is a parallelogram with AC and BD as diagonals. Then, A→C−B→D=
A4A→BB3A→BC2A→BDA→BIf ABCD is a parallelogram, then −−→AC−−−→BD=
A4−−→ABB3−−→ABC2−−→ABD−−→ABIf ABCDE is a pentagon, then
−−→AB+−−→AE+−−→BC+−−→DC+−−→ED+−−→AC is equal toA4−−→ACB2−−→ACC3−−→ACD5−−→AC
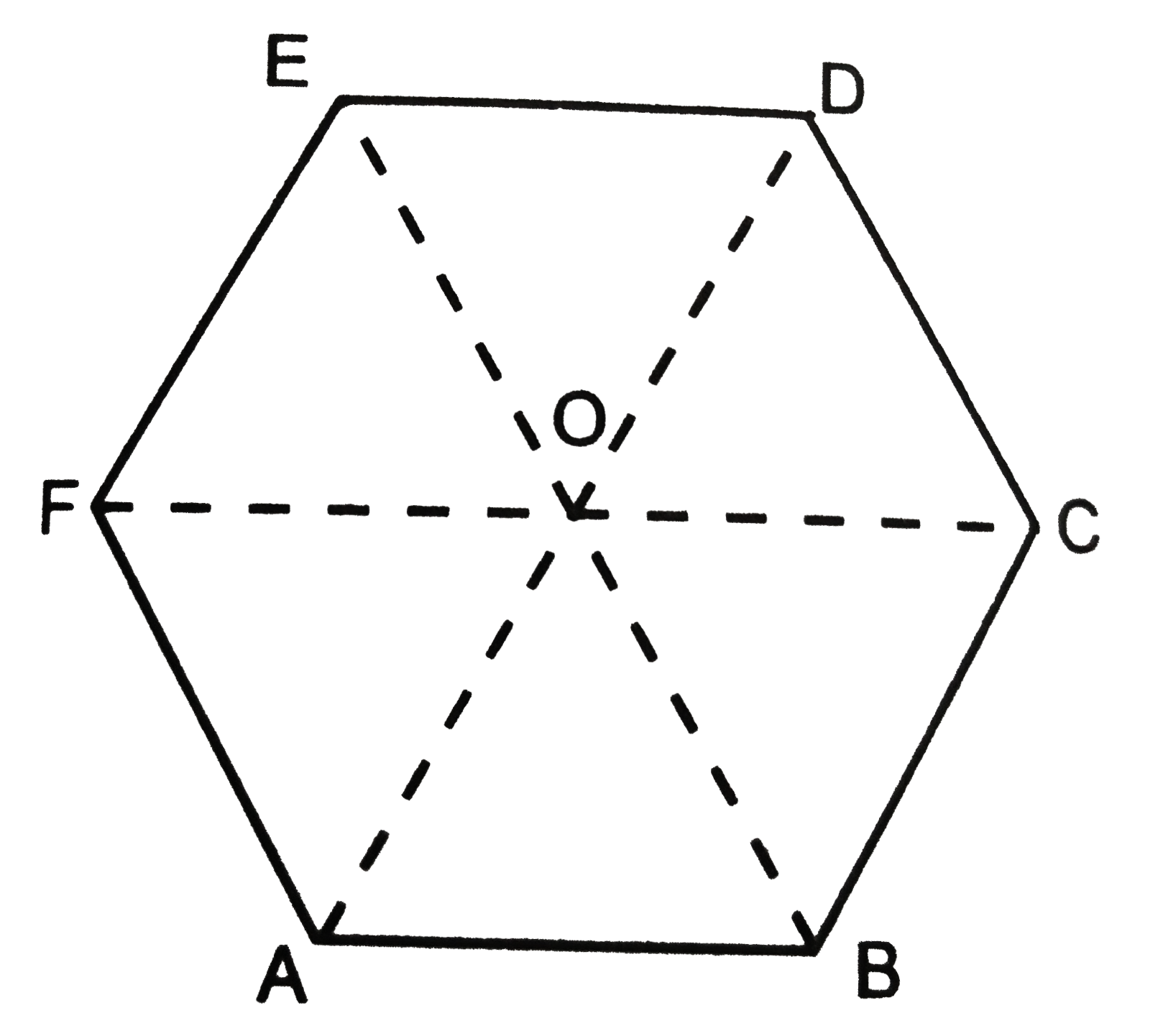
ABCDEF is a regular hexagon, Fig. 2 (c ) .65. What is the value of
(−−→AB+−−→AC+−−→AD+−−→AE+−−→AF?
 .
.
View SolutionLet ABCD is a parallelogram and →AC,→BD be its diagonal, then →AC+→BD is
View SolutionIf AC and BD are the diagonals of a quadrilateral ABCD, prove that its area is equal to 12∣∣∣−−→AC×−−→BD∣∣∣.
View SolutionABCD is a quadrilateral whose diagonals are AC and BD. Which one of the following is correct? (a) →BA+→CD=→AC+→DB (b) →BA+→CD=→BD+→CA (c) →BA+→CD=→AC+→BD (d) →BA+→CD=→BC+→AD
View SolutionIn Fig. ABCDEF is a ragular hexagon. Prove that
−−→AB+−−→AC+−−→AD+−−→AE+−−→AF=6−−→AO.
View Solution

