In an $Δ A B C$ as showin in Fig. 2 . (2) .71 (a) prove
that $\frac{a}{sin A} = \frac{b}{sin B} = \frac{C}{sin C}$ .

Video Solution

Text Solution

Verified by Experts

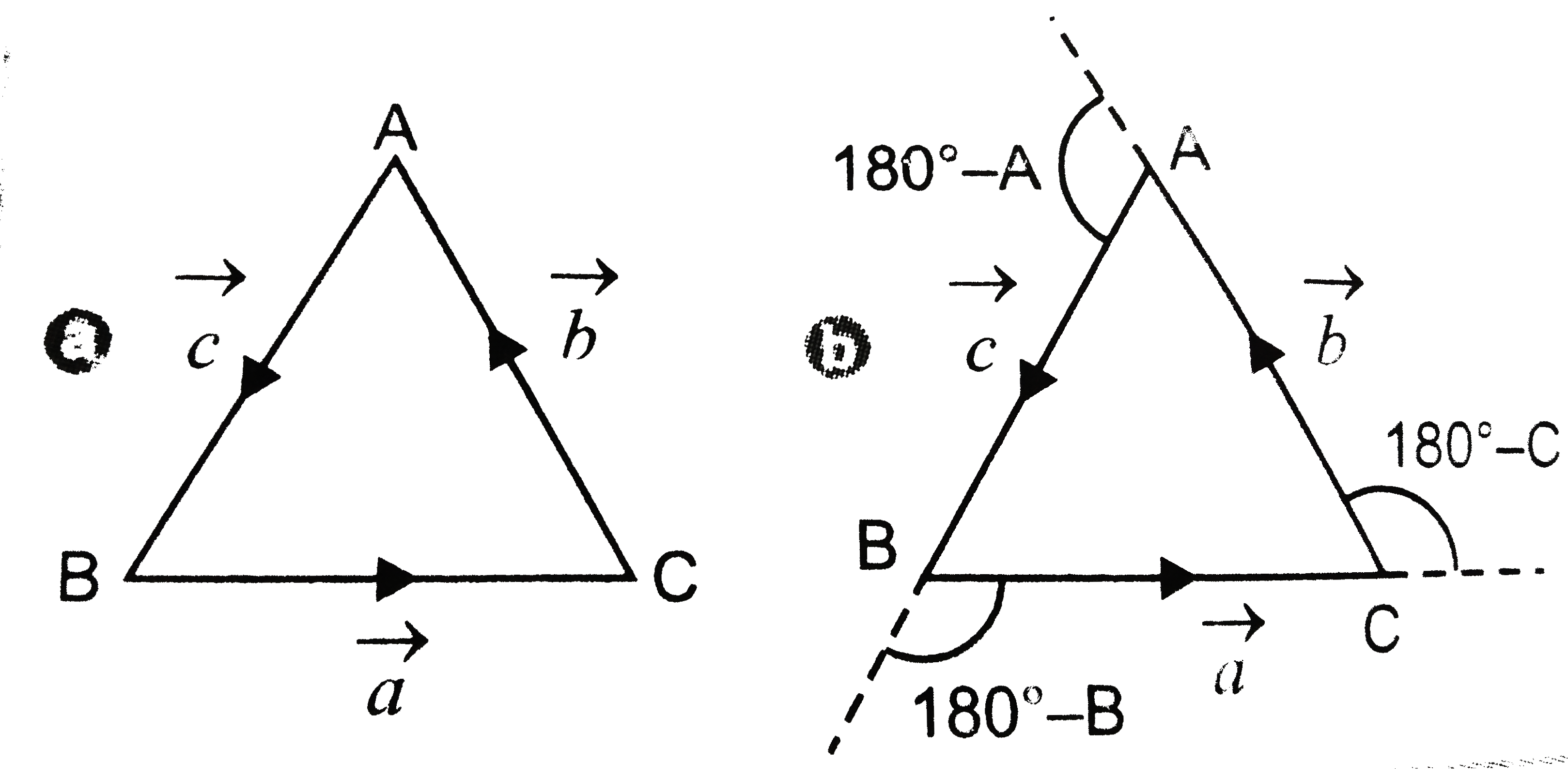
Refer to fig .2 (c ) . 71 (b). Mbrgt vectors $\to a, \to b and \to c$ are repesented by the three sides of a triangle taken in one order. Their resultant is zero. So
.
$\to a + \to b + \to c = 0$ ltvegt or $\to a + \to b = - \to c$
or $(\to a + \to b) \times x \to c = - \to c \times \to c = 0$
or $\to a \times \to c + \to b \to c = 0 or - \to c \times \to a + \to b + \to c = 0$
or $\to b \times \to c = \to c \times \to a$ ..(i)
Similarly we can get
$\to a \times \to b = \to b \times \to c$ (ii)
Form (i) and (ii),
$\to a \times \to b = \to b \times \to c = \to c \times \to a$
or $∣ ∣ \to a \times \to b ∣ ∣ = \to b \times \to c | = | \to c \times \to a ∣ ∣$
or $a b sin (180^{\circ} - C) = b c sin (80^{\circ} - A)$
$= c a sin (180^{\circ} - B) < b r > or a n sin C = sin A = c a sin B$
Dividing it by abc we get
$\frac{sin C}{c} = \frac{Sin A}{a} = \frac{sin B}{b}$
or $\frac{a}{sin A} = \frac{b}{sin B} = \frac{c}{sin C}$ (Proved)

Updated on:21/07/2023

|

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

PRADEEP-KINEMATICS-3 Con ceptual Problems

Home
Ask Doubt
Profile