Given vectors where O is the centre of circle circumscribed about , then find vector
The correct Answer is:
Step by step video, text & image solution for Given vectors barCB=bara, barCA=barb and barCO=barx where O is the centre of circle circumscribed about DeltaABC, then find vector barx by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 52 Videos
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise (Single Integer Answer Type Questions)
Explore 16 Videos
- PROBABILITYBook:ARIHANT MATHSChapter:PROBABILITYExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 55 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 21 Videos
Similar Questions
Knowledge Check
If the vectors ¯a,¯b and ¯c from the sides BC, CA and AB, respectively, of ΔABC, then
A¯a.¯b+¯b.¯c+¯c.¯a=0B¯aׯb=¯bׯc=¯cׯaC¯a.¯b=¯b.¯c=¯c.¯aD(¯aׯb)+(¯bׯc)+(¯cׯa)=¯0In the given figure, O is the centre of circle, ∠AOB=100∘. Find ∠BCD :
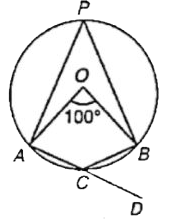 A80∘B60∘C50∘D40∘
A80∘B60∘C50∘D40∘In the given figure, O is the centre of the circle. ∠AOB=70∘, find ∠OCD :
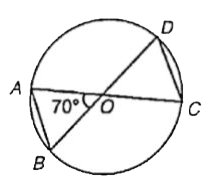 A70∘B55∘C65∘D110∘
A70∘B55∘C65∘D110∘
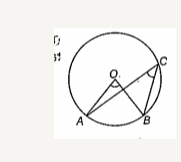
In the given figure, O is the centre of the circle and ∠ACB=25∘ Find ∠AOB
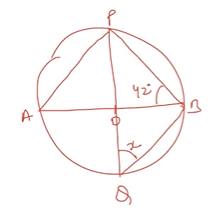
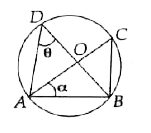
View SolutionIn the figure given below O is the centre of the circle, if θ=60∘, then find angle α
View SolutionIf the volume of parallelepiped determined by vectors (2¯aׯb),(¯bׯ¯¯¯3c) and 5(¯cׯa) is equal to the volume of the parallelepiped determined by vectors 5(¯a+¯b),6(¯b+¯c) and 2(¯c+¯a), then find the volume of parallelepiped determined by vectors ¯,¯b and ¯c in cubic units.
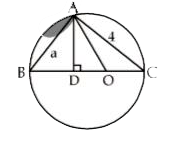
View SolutionIn a given figure, if AB = a, AC = 4 cm, where O is centre of circle and a point D is on BC such that AD ⊥ BC then find length of OD?
View SolutionIf OA=30 cm, then find the radius OB (in cm), where o is the centre of circle.

View Solution