Given, the angles A, B and C of △ABC. Let M be the mid-point of segment AB and let D be the foot of the bisector of ∠C. Find the ratio of AreaOf△CDMAreaof△ABC and also cosϕ=cos∠DCM.
Text Solution
The correct Answer is:sinA−sinB2(sinA+sinB)
|
Topper's Solved these Questions
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 52 Videos
- PRODUCT OF VECTORSBook:ARIHANT MATHSChapter:PRODUCT OF VECTORSExercise:Exercise (Single Integer Answer Type Questions)
Explore 16 Videos
- PROBABILITYBook:ARIHANT MATHSChapter:PROBABILITYExercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 55 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES Book:ARIHANT MATHSChapter:PROPERTIES AND SOLUTION OF TRIANGLES Exercise:Exercise (Questions Asked In Previous 13 Years Exam)
Explore 21 Videos
Similar Questions
Knowledge Check
Let D be the mid-point of a straight line AB and let C be a point different from D such that AC=BC, then.
AAC⊥ABB∠BDC=90∘C∠BDC is acuteD∠BDC>90∘Let D be the mid-point of a straight line AB and let C be a point different from D such that AC=BC, then.
AAC⊥ABB∠BDC=90∘C∠BDC is acuteD∠BNDC>90∘Let ABC be an acute-angled triangle and let D be the midpoint of BC. If AB = AD, then tan(B)/tan(C) equals
A√2B√3C2D3
In ABC, D and E are the mid-points of AB and AC respectively. Find the ratio of the areas of ADE and ABC .
View Solution△ABC is right angled at A and AD⊥BC. If BC = 13 cm and AC= 5 cm. find the ratio of the areas of △ABCand△ADC.
View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC
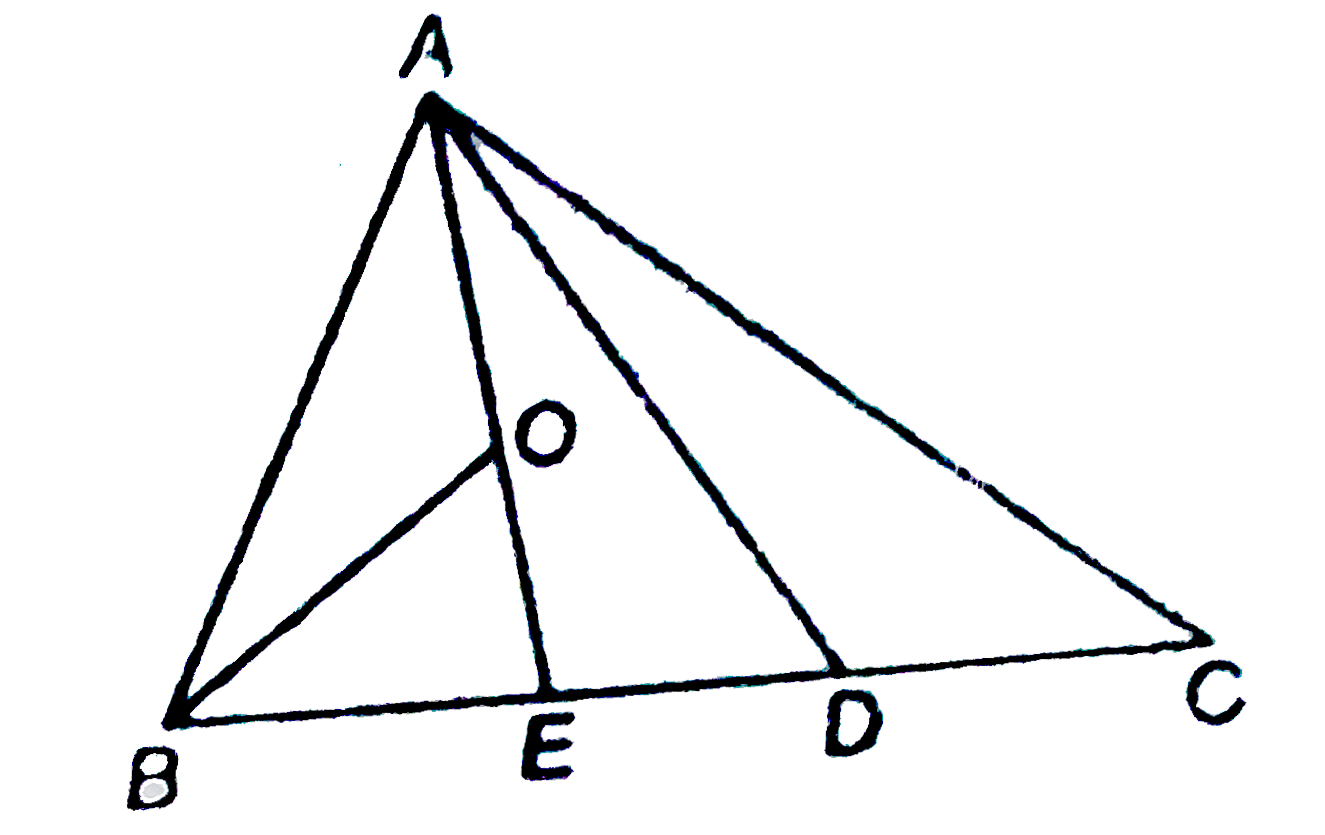
View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC

View SolutionIf D, E and F are the mid-points of the sides of a △ABC , the ratio of the areas of the triangles DEF and ABC is .......
View Solution

