Two physical pendulums perform small oscillations about the same horizontal axis with frequencies ω1 and ω2 . Their moments of inertia relative to the given axis are equal to I1 and I2 respectively. In a state of stable equilibium the pendulums were fastened rigifly together. What will be the frequency of small oscillations of the compound pendulum ?
When the two pendulums are joined rigidly and set to osciallate, each exert torques on the other, these torques are equal and opposite. We write the law of motion for the two pendulums as
I1..θ=−ω21I1θ+G
I2..θ=−ω22I2θ−G
where ±G is the torque of mutual interactions. We have written forces on each pendulum in the absence of the other as −ω22I1θ and −ω22I2θ respectively. Then
..θ=−I1ω21+I2ω22I1+I2θ=−ω2θ
Hence ω=√I1ω21+I2ω22I1+I2
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Electric Oscillations
Explore 56 Videos
- OSCILLATIONS AND WAVESBook:IE IRODOV, LA SENA & SS KROTOVChapter:OSCILLATIONS AND WAVESExercise:Elastic Waves
Explore 39 Videos
- OPTICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:OPTICSExercise:Exercise
Explore 2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
Similar Questions
A physical pendulum performs small oscillations about the horizontal axis with frequency ω1=15.0s−1. When a small body of mass m=50g is fixed to the pendulum at a distance l=20cm below the axis, the oscillation frequency becomes equal to ω2=10.0s−1. Find the moment of inertia of the pendulum relative to the oscillation axis.
View SolutionFind the period of small torsional oscillational of a system consisting of two discs slipped oon a thin rod with rod with torsional coefficient k. The moments of inertia of discs relative to the rod's axis are equal to I1 and I2.
View Solution
Knowledge Check
Two disc has same mass rotates about the same axis with their densities ρ1 and ρ2 respectively such that (ρ1>ρ2), then the relation between I1 and I2 will be
AI1<I2BI1=I2CI1>I2DI1=2I2Two loops P and Q are made from a uniform wire. The radii of P and Q are R1 and R2, respectively, and their moments of inertia about their axis of rotation are I1 and I2, respectively. If I1I2=4, then R2R1 is
A423B413C4−23D4−13Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies ω1 and ω2 and have total energies E1 and E2 repsectively. The variations of their momenta p with positions x are shown in figures. If ab=n2 and aR=n, then the correc t equation(s) is (are) :
 AE1ω1=E2ω2Bω2ω1=n2Cω1ω2=n2DE1ω1=E2ω2
AE1ω1=E2ω2Bω2ω1=n2Cω1ω2=n2DE1ω1=E2ω2
Two horizontal discs rotate freely about a vertical axis passing through their centres. The moments of inertia of the discs relative to this axis are equal to I1 and I2, and the angular velocities to ω1 and ω2. When the upper disc fell on the lower one, both discs began rotating, after some time, as a single whole (due to friction). Find:
(a) teh steady-state angular rotation velocity of the discs,
(b) the work performed by the friction forces in this process.
View SolutionFind the frequency of small oscillations of the arrangement illustrated in figure. The radius of the pulley is R, its moment of inertia relative to the rotation axis is I, the mass of the body is m, and the spring stiffness is x.The mass of the thread and the spring is negligible , the thread does not slide over the pulley, there is no friction in the axis of the pulley
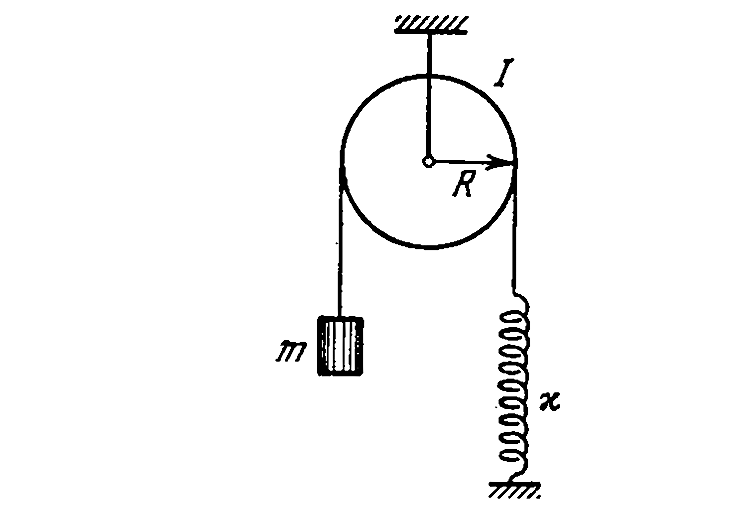
View SolutionA wave of angular frequency ω propagates so that a certain phase of oscillation moves along x-axis, y-axis, z-axis with speeds c1c2 and c3 respectively.
View SolutionTwo bodies have their moments of inertia I and 2I respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio.
View SolutionTwo bodies have their moments of inertia I and 2I, respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular velocity will be in the ratio
View Solution

