Calculate the mutual inductance of a long straight wire and a rectangular frame with sides a and b. The frame and the wire lie in the same plan, with the side b being closent to the wire, separated by a distance l from it and oriented parallel to it.
Here, B=μ0I2πr at a distance r from the wire. The flux through the frame is obtained as,
Φ12=∫a+llμ0I2πrbdr=μ0b2πI In (1+al)
Thus, L12=Φ12I=μ0b2πIn(1+al)

Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Motion Of Charged Particle In Magnetic Field
Explore 36 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
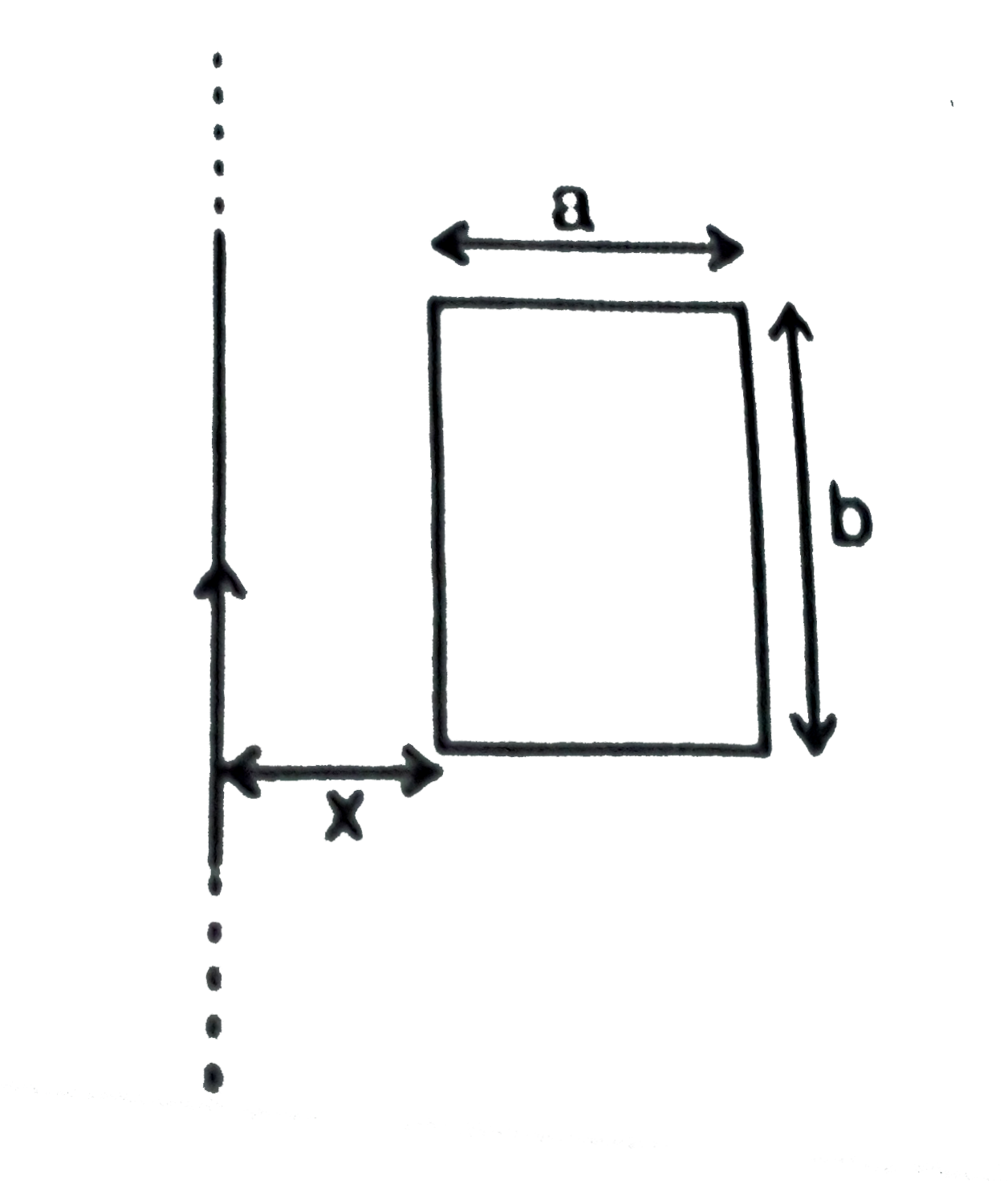
Find the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.
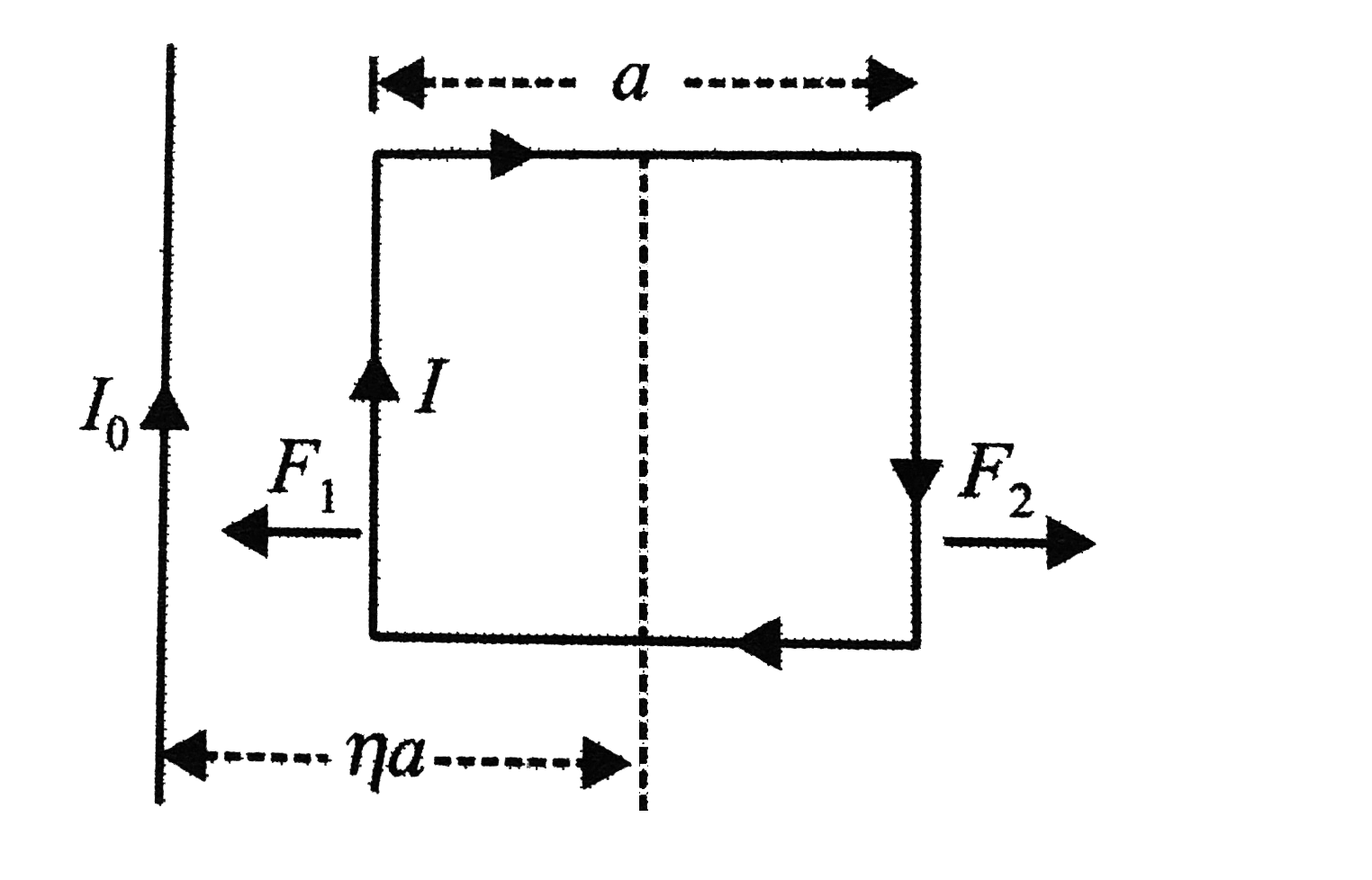
View SolutionA square frame carrying a current I is located in the same plane as a long straight wire carrying a current I0 The frame side has a length a. The axis of the frame passing through the midpoints of the opposite sides is parallel to the wire and is separated from it by the distance which is η times greater than the side of the frame. Find

(a) Force acting on the frame
(b) The mechanical work to be performed in order to turn the frame through 180∘ about its axis, with the currents maintained constant.
View Solution
Knowledge Check
The mutual inductance between the rectangular loop and the long straight wire as shown in figure is M.
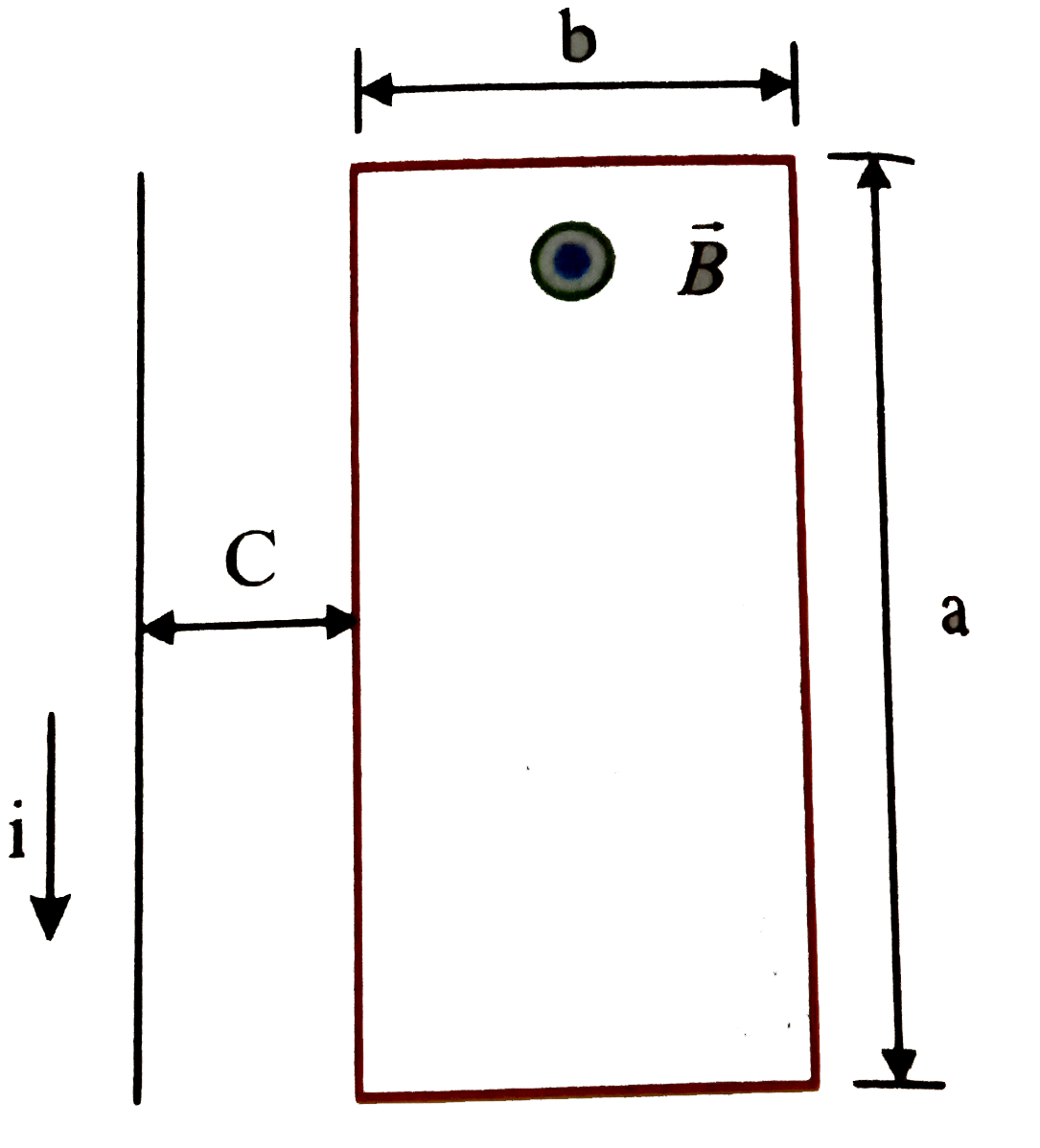 AM= zeroBM=μ0a2πln(1+cb)CM=μ0a2πln(a+bb)DM=μ0a2πln(1+bb)
AM= zeroBM=μ0a2πln(1+cb)CM=μ0a2πln(a+bb)DM=μ0a2πln(1+bb)The mutual inductance between the rectangular loop and the long straight wire as shown in figure is M.
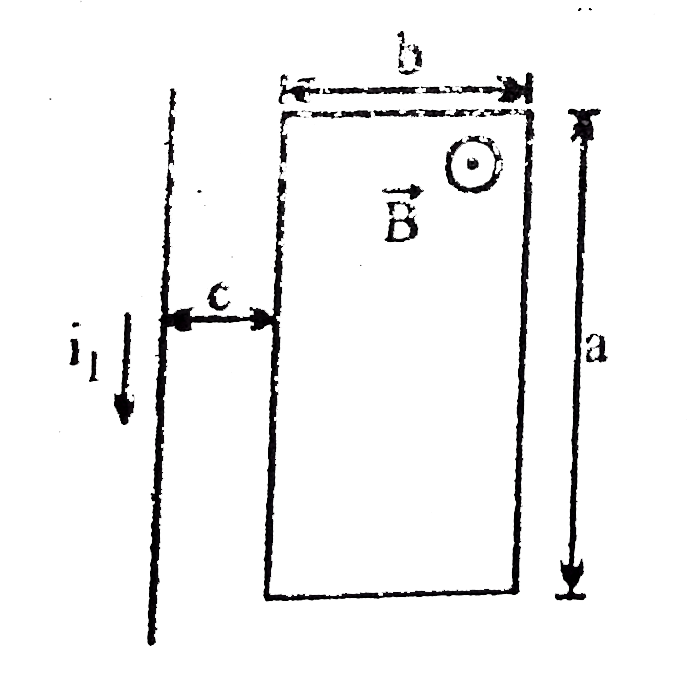 AM=ZeroBM=μ0a2πIn(1+cb)CM=μ0b2πIn(a+cb)DM=μ0a2πIn(1+bc)
AM=ZeroBM=μ0a2πIn(1+cb)CM=μ0b2πIn(a+cb)DM=μ0a2πIn(1+bc)If same current I passing through two parallel wires separated by a distance b, then force per unit length will he
Aμ04π2I2bBμ0I4πbCμ0I24πb2Dμ0I24πb
A square frame carrying a current I=0.90A is located in the same plane as a long straight wire carrying a current I0=5A, The frame side has a length a=8cm. The axis of the frame passing through the mid-point of the opposite sides is parrallel to the wire and is separated form it by a distance h=15 times greater tahn the side of the frame.
Find:
(a) ampere force acting on the frame.
(b) The machanical work to be performed in order to turn the frmae through 180∘ about its axis, with the current maintained constant.
View SolutionA square frame carrying a current I=0.9A is located in the same plane as a long straght wire carrying a current, I0=5.0A. The frame side has a length a=8.0cm. The axis of the frame passing thorugh the midpoints of opposite sides is parallel to the wire and is separated from it by the distance which is η=1.5 times greater than the side of the frame. FInd:
(a) Ampere force acting on the frame,
(b) the mechnical work to be performed in order to turn the frame throguh 180∘ about its axis, with the currents maintained constant.
View SolutionA square frame carrying a current I=0.9A is located in the same plane as a long straght wire carrying a current, I0=5.0A. The frame side has a length a=8.0cm. The axis of the frame passing thorugh the midpoints of opposite sides is parallel to the wire and is separated from it by the distance which is η=1.5 times greater than the side of the frame. FInd:
(a) Ampere force acting on the frame,
(b) the mechnical work to be performed in order to turn the frame throguh 180∘ about its axis, with the currents maintained constant.
View SolutionThe magnetic induction due to an infinitely long straight wire carrying a current i at a distance r from wire is given by
View SolutionTwo thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
View Solution

