Find the appoximate formula expressing the mutual inductance of two thin coaxial loops of the same radius $a$ if their centres are separated by a distance $l$ , with $l > > a$

Video Solution

Text Solution

Verified by Experts

If a current $I$ flows is one of the coils, the magnetic field at6 the centre of the other coil is,
$B = \frac{μ_{0} a^{2} I}{2 {(l^{2} + a^{2})}^{3 / 2}} = \frac{μ_{0} a^{2} I}{2 l^{3}}$ , as $l > > a$
The flux associated with the secound coil is then appoximately $μ_{0} π a^{4} I / 2 l^{3}$
Hence, $L_{12} = \frac{μ_{0} π a^{4}}{2 l^{3}}$

Updated on:21/07/2023

The approximate formula expressing the formula of mutual inductance of two coaxial loops of the same redius $a$ when their centers are separated by a distance $l$ with $l > > a$ is
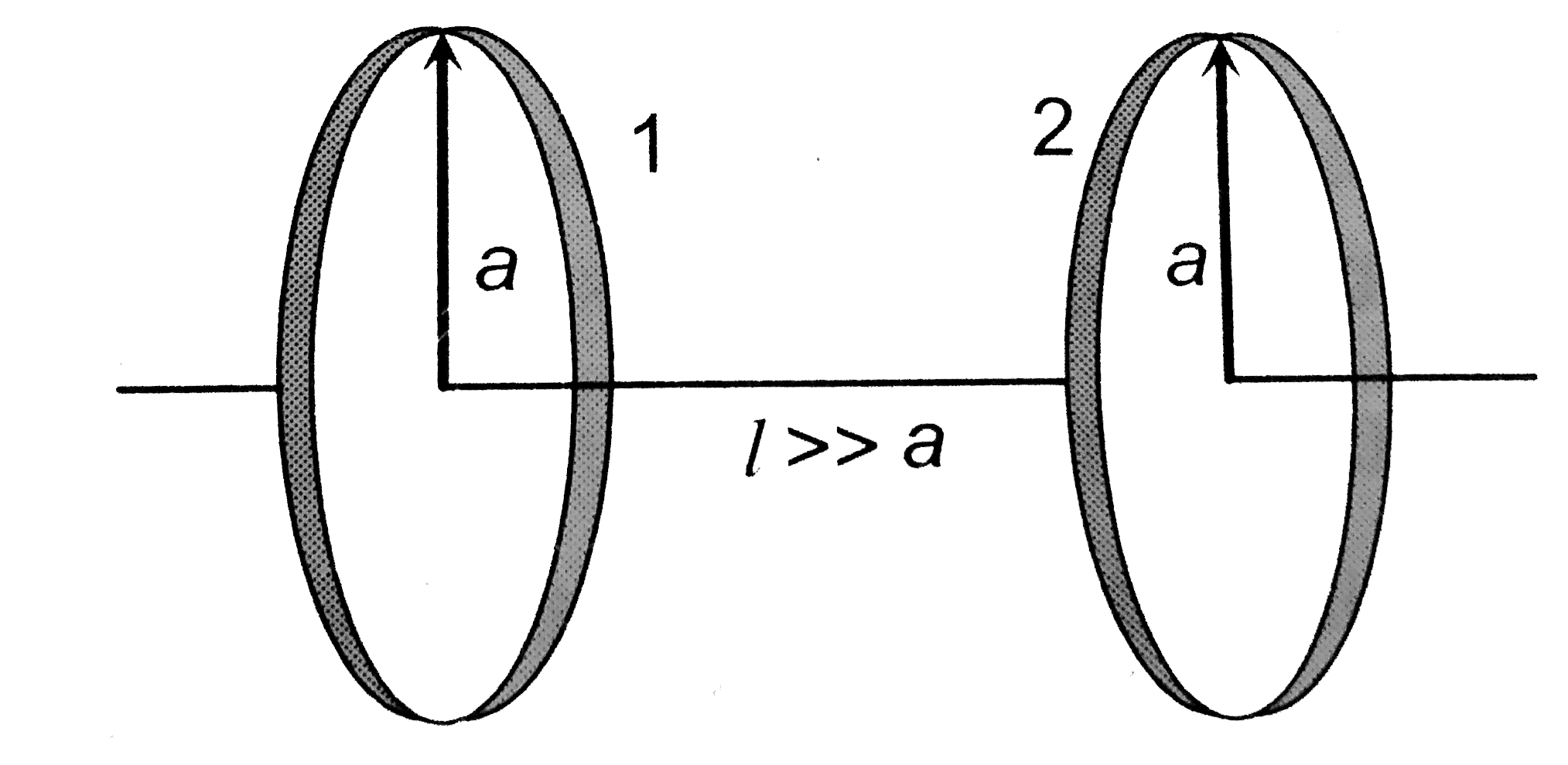
A $\frac{1}{2} \frac{μ_{0} π a^{4}}{l^{3}}$
B $\frac{1}{2} \frac{μ_{0} a^{4}}{l^{2}}$
C $\frac{μ_{0}}{4 π} \frac{π a^{4}}{l^{2}}$
D $\frac{μ_{0}}{π} \frac{a^{4}}{l^{3}}$
What is the mutual inductance of a two-loop system as shown with centre separation l

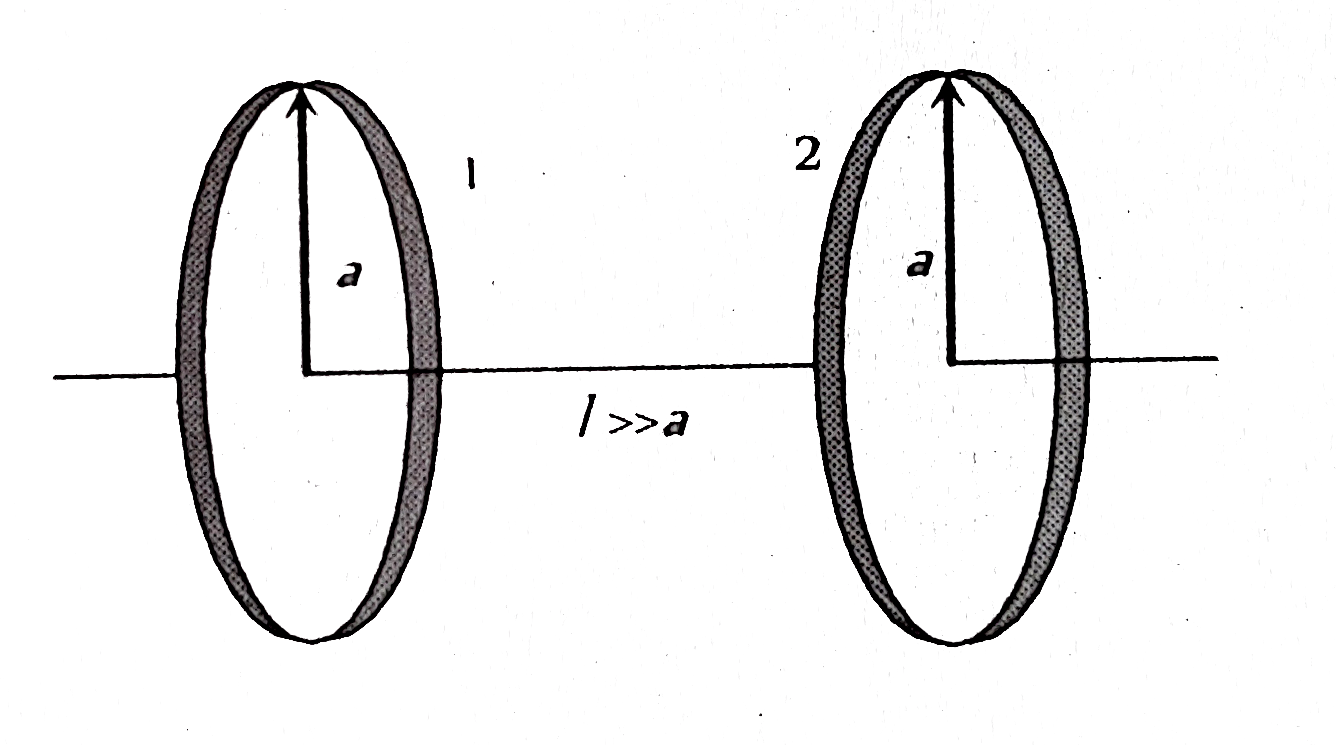A $\frac{μ_{0} π a^{4}}{8 l^{3}}$
B $\frac{μ_{0} π a^{4}}{4 l^{3}}$
C $\frac{μ_{0} π a^{4}}{6 l^{3}}$
D $\frac{μ_{0} π a^{4}}{2 l^{3}}$
Mutual inductance of two coils depends on their self inductance $L_{1}$ and $L_{2}$ as :
A $M_{12} = L_{1} / L_{2}$
B $M_{12} = L_{2} / L_{1}$
C $M_{12} = \sqrt{L_{1} L_{2}}$
D $M_{12} = \sqrt{L_{1} / L_{2}}$