Find the interaction energy of two loops carrying currents I1 and I2 if both loops are shaped as circles of radii a and b, with a<<b. The loops centres are located at the same point and their planes from an angle θ between them.
We can think of the smaller coil as consituting a magnet of dipole moment,
pm=πa2I1
Its direction is normal to the loop and makes and angle θ with the direction of the magnetic field, due to the bigger loop. This magnetic field is,
B2=μ0L22b
The interactiion energy has the magnitude,
|W|=μ0I1I22bπa2cosθ
Its sign depends on the sense of the currents.
Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Motion Of Charged Particle In Magnetic Field
Explore 36 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
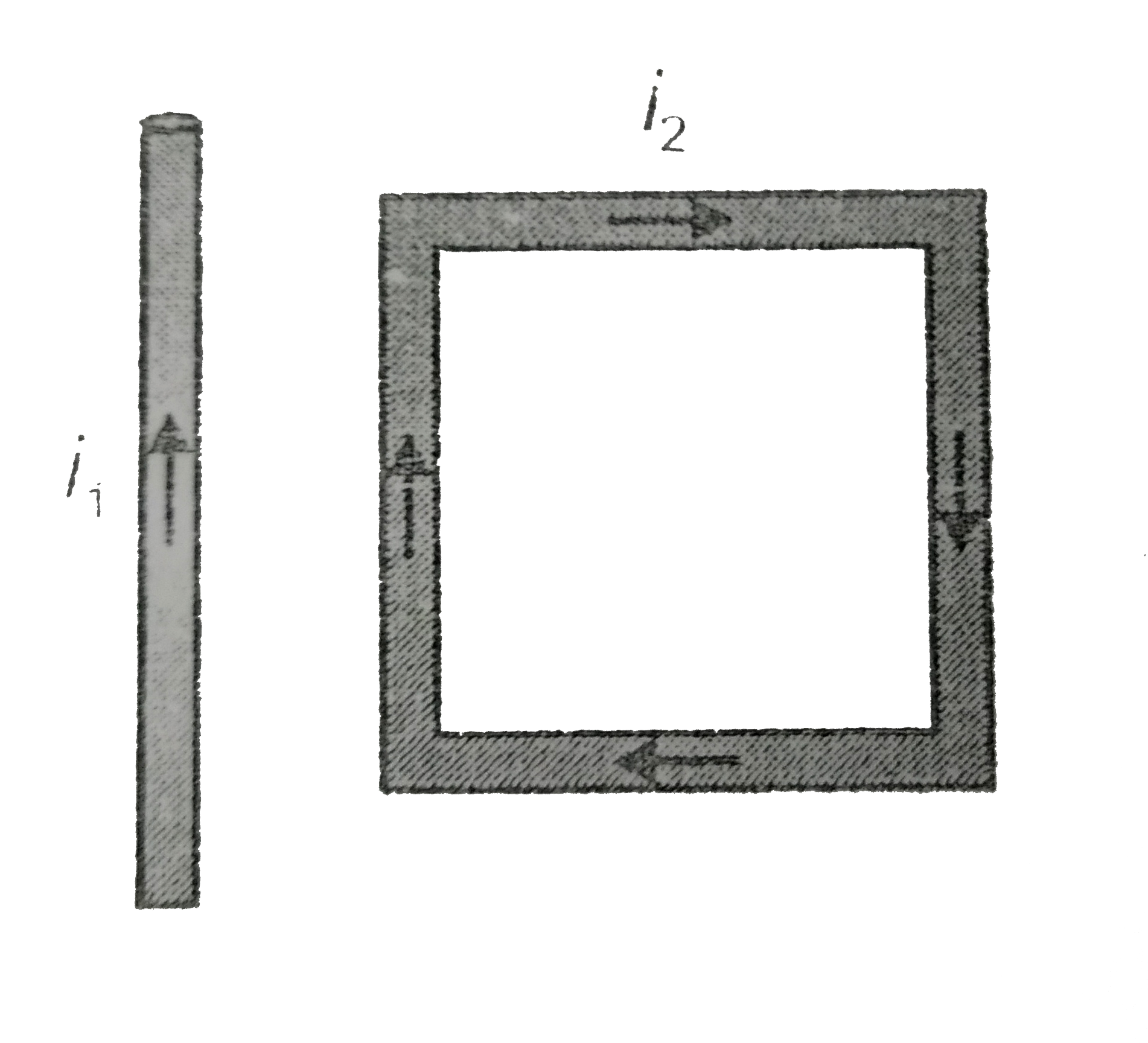
A rectangular loop carrying a current i2 situated near a long straight wire carrying a steady current i1. The wire is parallel to one of the sides of the loop and is in the plane of the loop as shown in the figure. Then the current loop will
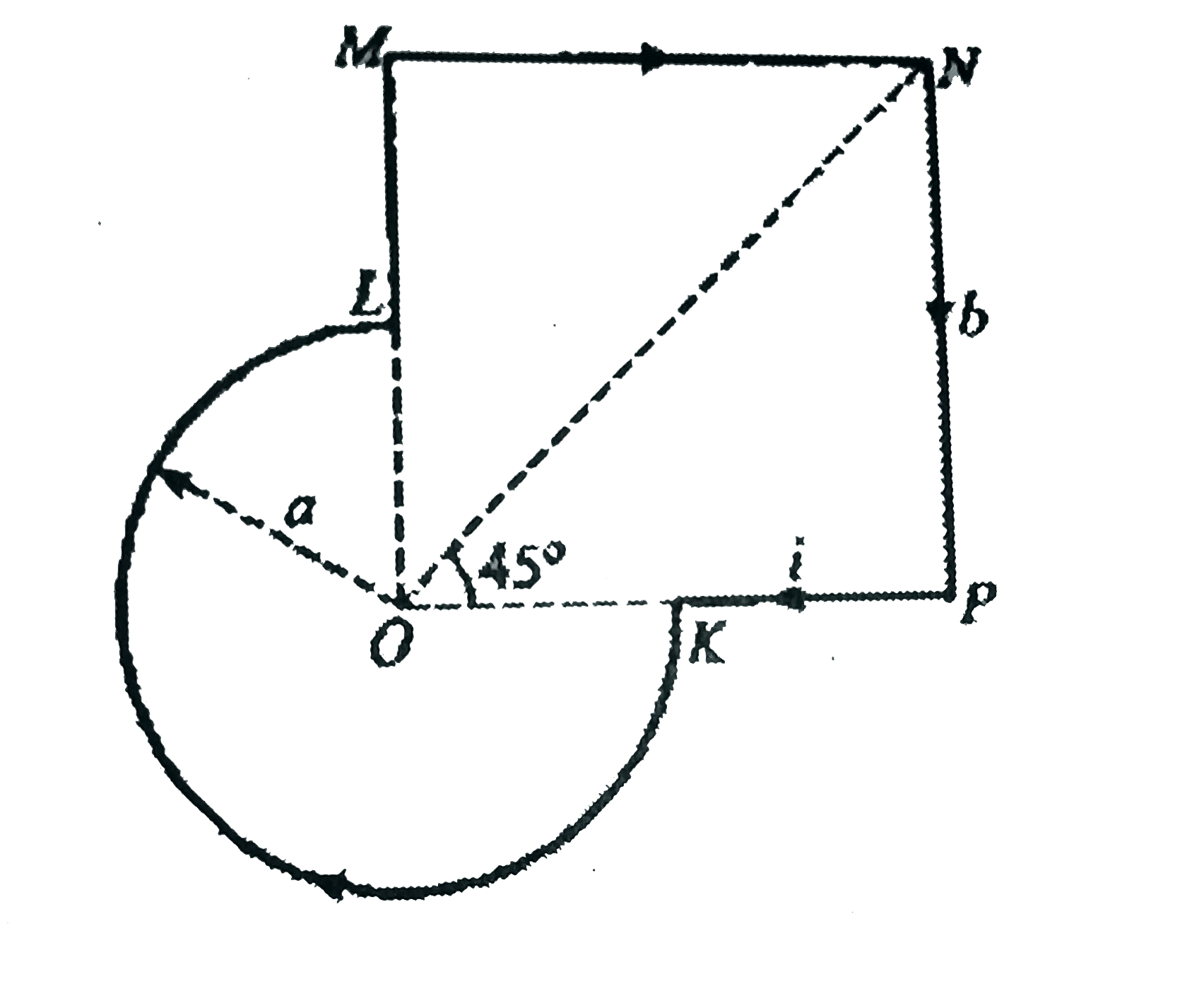
View SolutionFind the magnetic induction at the point O due to the loop current I in the two cases given below. The shape of the loop are illustrated as
(a) In figure-4.17 (a), the radii A and b, as well as the angle ϕ are known.

(b) In figure 4.17 (b), the radius a and the side b are known.
View Solution
Knowledge Check
Shown in the figure is a rectangular loop of conductor carrying a current i. The length and breath of the loop are respectively a and b. The magnetic field at the centre of loop is -
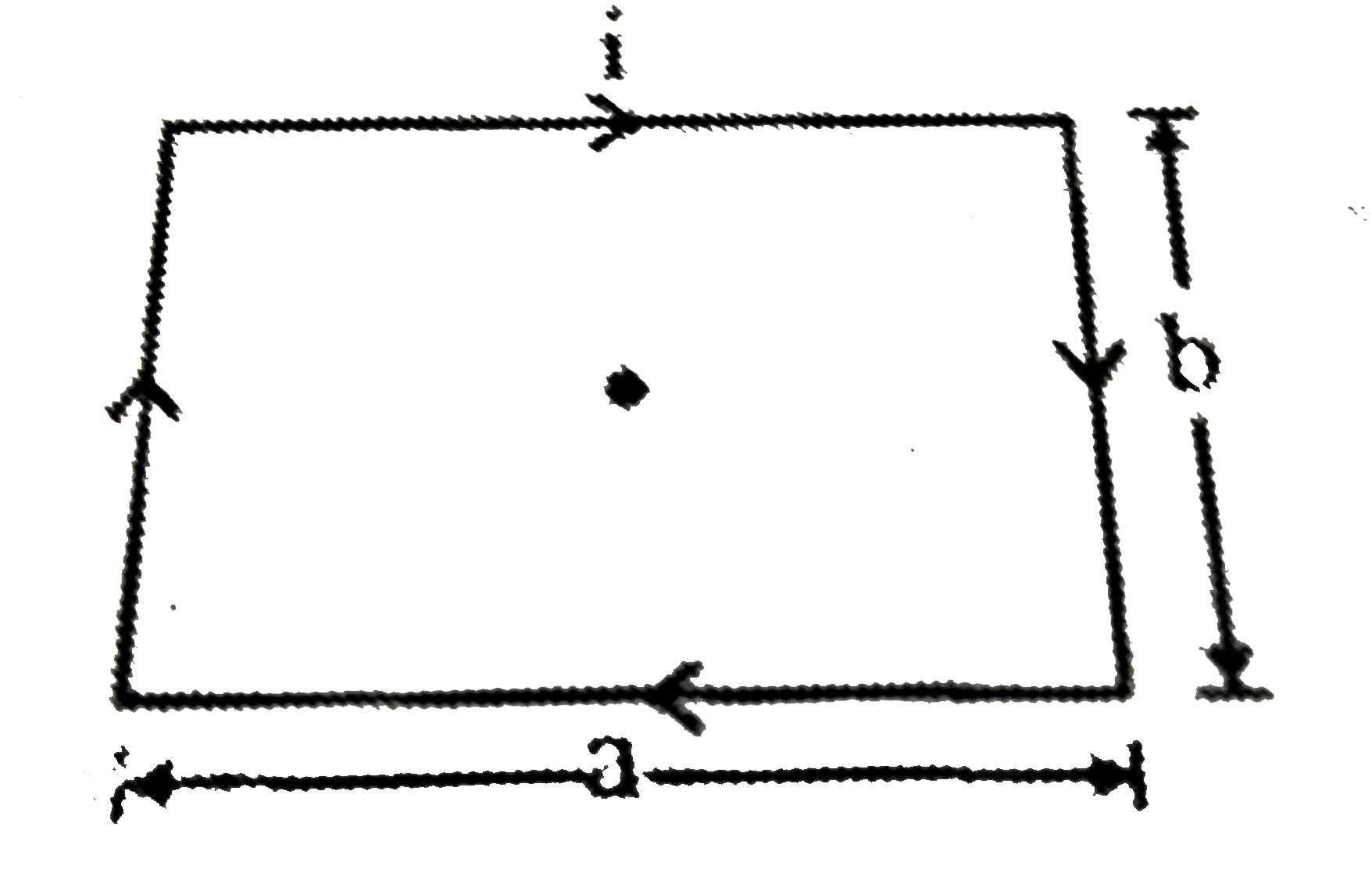 Aμ0i(a+b)2π√a2+b2Bμ0iab2π√a2+b2Cμ0i(a+b)π√a2+b2D2μ0i√a2+b2πab
Aμ0i(a+b)2π√a2+b2Bμ0iab2π√a2+b2Cμ0i(a+b)π√a2+b2D2μ0i√a2+b2πabA loop carrying current I has the shape of a regular polygon of n sides. If R is the distance from the centre to any vertex, then the magnitude of the magnetic induction vector →B at the centre of the loop is –
Anμ0I2πRtan.πnBμ0I2RCnμ0I2πRtan.2πnDμ0IπRtan.πnIn the following figure a current loop is shown which is made from two circular arcs of radii a and b(a<b), connected by radial wires. Calculate the magnetic field at the centre O.
 Aμ0iθ4πab(b−a), inwardsBμ0iθ4πab(b−a), outwardsCμ0iθ3πab(b−a), inwardsDZero
Aμ0iθ4πab(b−a), inwardsBμ0iθ4πab(b−a), outwardsCμ0iθ3πab(b−a), inwardsDZero
Two circular loops A and B of radii R and 4R are kept concentrically in the same plane. The loops carry currents I1 and I2 respectively. If the magnetic field at a point on the common axis of the loops at a distance 2R from their common centre is zero, the ratio I1I2 is _________.
View SolutionA circular loop of radius R carries a current I. Another circular loop of radius r(ltltR) carries a current I. The plane of the smaller loop makes an angle of 30^@ with that of the larger loop. The planes of the two circles are at right angle to each other. Find the torque acting on the smaller loop.
View SolutionA square loop of side L carries a current I. Another smaller square loop of side l(l<<L) carrying a current i is placed inside the bigger loop such that they are coplanar with their centre coinciding. If the currents in the loops are in the same direction, the magnitude of the torque on the smaller loop is
View SolutionA long straight wire is carrying current I1 in +z direction, The x-y plane contains a closed circular loop carrying I1 and not encircling the straight wire. The force on the loop will be
View SolutionA long current carrying wire , carrying current I1 such that I1 is flowing out from the plane of paper is placed at O. A steady state current I2 is flowing in the loop ABCD
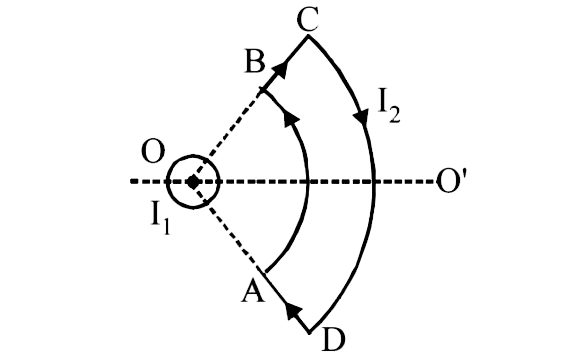
View Solution

