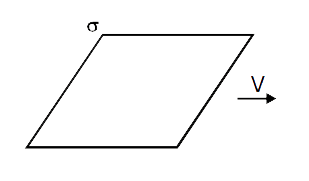
A large plate of non-ferromagnetic material moves with a constant velocity v=90cm/s in a unifrom magnetic field with induction B=50mT as shown in Fig. Find the surface density of electric charges appearing on the plate as a result of its motion.

Within the plate, there will appear a (→v×→B) force, which will cause charges inside the plate to drift, until a countervalling electric field is set up. This electric field is related to B, byE=eB since v&B are mutually perpendicular, and E is perpendicular to both. THe charge density ±σ, on the force of the plate, producing this electric field, is given by
E=σε0 or σ=ε0vB=0.40pC/m2
Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Motion Of Charged Particle In Magnetic Field
Explore 36 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
A charged particle moves along a circle of radius r=100mm in a unifrom magnetic field with induction B=10.0mT. Find its velocity and perios of revolution if that particle is
(a) a non-relativistic proton,
(b) a relativistic electron.
View SolutionA proton moves at a constant velocity of 50ms along the x-axis, in uniform electric and magnetic fields. The magnetic field is B=(2.0mT)ˆj. What is the electric field?
View Solution
Knowledge Check
A large plate with uniform surface charge density σ is moving with constant speed v as shown in the figure. The magnetic field at a small distance from plate is
 Aμ0σv in magnitudeBμ0σv2 in magnitudeCperpendicular to plateDparallel to plate
Aμ0σv in magnitudeBμ0σv2 in magnitudeCperpendicular to plateDparallel to plateA parallel plate capacitor is moving with a velocity of 25ms−1 through a uniform magnetic field of 4.0T as shown in Fig. If the electric field within the capacitor plates is 175NC−1 and the plate area is 25×10−7m2, then the magnetic force experienced by the positive charge plate is
 A8.85×10−13N directed out of the plane of the paperBzeroC8.85×10−15N directed out of the plane of the paperDnone of above
A8.85×10−13N directed out of the plane of the paperBzeroC8.85×10−15N directed out of the plane of the paperDnone of aboveA charge particle of charge q and mass m is moving with velocity v as shown in fig In a uniform magnetic field B along -ve z-direction.Select the correct alternative (s).
 AVelocity of the particle when it comes out form the magnetic field is →v−vcos60∘ˆi+vsin60∘ˆjBTime for which the particle was in magnetic field is πm3qBCDistance travelled in magnetic field is πmv3qBDNone of these
AVelocity of the particle when it comes out form the magnetic field is →v−vcos60∘ˆi+vsin60∘ˆjBTime for which the particle was in magnetic field is πm3qBCDistance travelled in magnetic field is πmv3qBDNone of these
A thin wire AC shaped as a semi-circle of diaameter d=20cm rotates with a constant angular velocity ω=100 rad/s in a unifrom magnetic field of induction B=5.0mT, with ω↑↑B. The rotation axis passes through the end A of the wire and is perpendicular to the diameter AC. Find the value of a line intergal ∫Edr along the wire from point A to C. Generalize the botained result.
View SolutionA non-relativistic point charge q moves with a constant velocity v. Using the field transformation formula. Find the magnetic induction B produced by this charge at the point whose position relative to the charge is determind by the radius vector r.
View SolutionA parallel plate capacitor with area of each plate equal to S and the separation between them to d is put into a stream of conducting liquid with respectivity ρ. The liquid moves parallel to the plates with a constant velocity v. The whoel system is located in a unifrom magentic field of induction B, vector B being parallel to the plates are interconnected by means of an exteranal resistance R. What amount of power is genrated in that resistance? At what value of R is the generated power the highest? What is this highest power equla to ?
View SolutionA particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View SolutionWhen a charged particle moving with velocity →v is subjected to a magnetic field of induction →B, the force on it is non-zero. This implies that:
View Solution

