In the circuit shown in Fig. emfE , a resistance R, and coil inductances L1 and L2 are known. The internal resistance of the source and the coil resistances are neglible. Find the steady-state currents in the coils after the swich Sw was shorted.

The equations are,
L1di1dt=ξ−R(i1+i2)
Then, ddt(L1i1−L2i2)=0
or, L1i1−L2i2 = constant
But initally at t=0,i1=i2=0
so constant must be zero and at all times,
L1i1=L2i2
In the final steady state, current must obviusly be i1+i2=ξR . Thus is steady state,
i1=ξL2R(L1+L2) and i2=ξL1R(L1+L2)

Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Motion Of Charged Particle In Magnetic Field
Explore 36 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Constant Magnetic Fiels - Magnetics
Explore 69 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
Two coils of self inductance L1 and L2 are connected in parallel and then connected to a call of emf ε and internal resistance - R. Find the steady state current in the coils.
View SolutionTwo coils of self inductance L1 and L2 are connected by in parllel and the then to cell of emf ε and of resistance R throught a Key . Find the instantaneous current throught L after the key is closed .
View Solution
Knowledge Check
In the circuit shown in the figure The steady state currents i1andi2 in the coils after the switch S is closed are
 Ai1=EL2R(L1+L2)Bi1=EL1R(L1+L2)Ci2=EL2R(L1+L2)Di2=E√L1L2RL2
Ai1=EL2R(L1+L2)Bi1=EL1R(L1+L2)Ci2=EL2R(L1+L2)Di2=E√L1L2RL2In the circuit, a battery of emf E, a resistance R and inductance coil L1andL2 and switch S are connected as shown. In Fig. Initially the switch is open
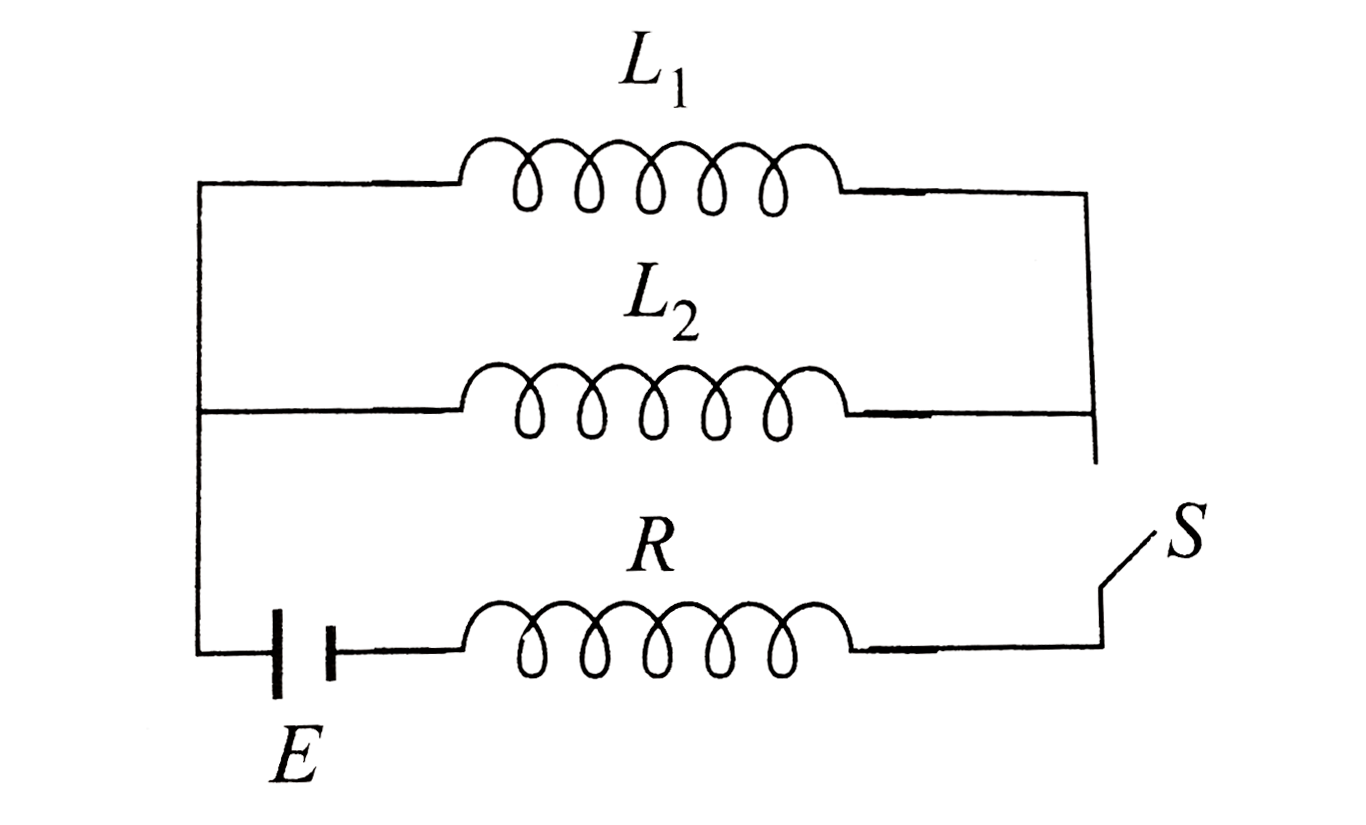 AThe time constant of the circuit is 1RL1L2L1+L2BSteady state current in the inductor L1is(EL_(2))/(R(L_(1)+L_(2)))CSteady state current in the inductor L2 is EL1R(L1+L2)DIn steady the total energy stored in the inductor coils is 12L1L2L1+L2E2R2
AThe time constant of the circuit is 1RL1L2L1+L2BSteady state current in the inductor L1is(EL_(2))/(R(L_(1)+L_(2)))CSteady state current in the inductor L2 is EL1R(L1+L2)DIn steady the total energy stored in the inductor coils is 12L1L2L1+L2E2R2A coil resistance R and inductance L is connected to a battery of emf E volt. The final current in the coil is
AERBELC√(ER2+L2)D√(ELR2+L2)
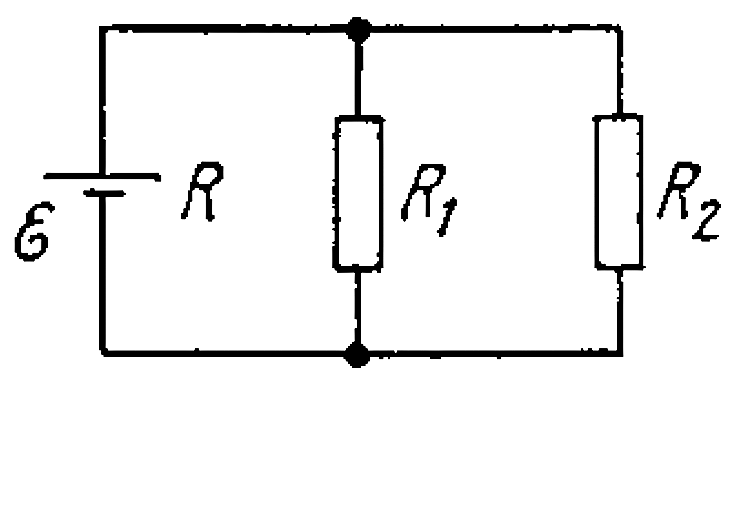
In the circuit shown in Fig. the emf of the sources is equal to ξ=5.0V and the resistances are equal to R1=4.0Ω and R2=6.0Ω. The internal resistance of the source equals R=1.10Ω. Find the currents flowing through the resistances R1 and R2.
View SolutionA coil inductance L and resistance R is connected to a constant voltage source. How soon will the coil current attains η(η<1) fraction of the steady state value?
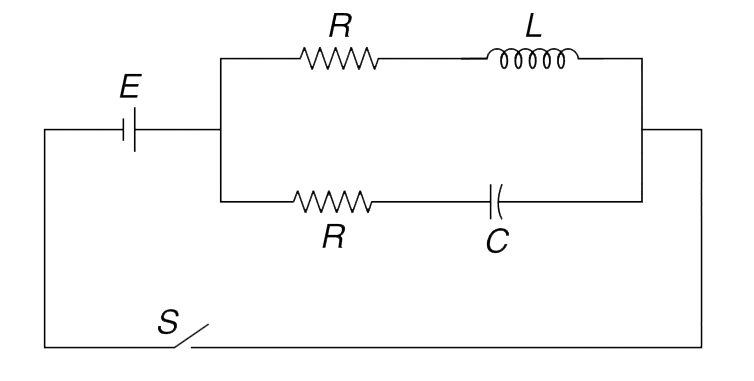
View SolutionIn the circuit shown, find the value of resistance R in terms of inductance L and capacitance C such that the current through the cell remains constant forever after the switch is closed.
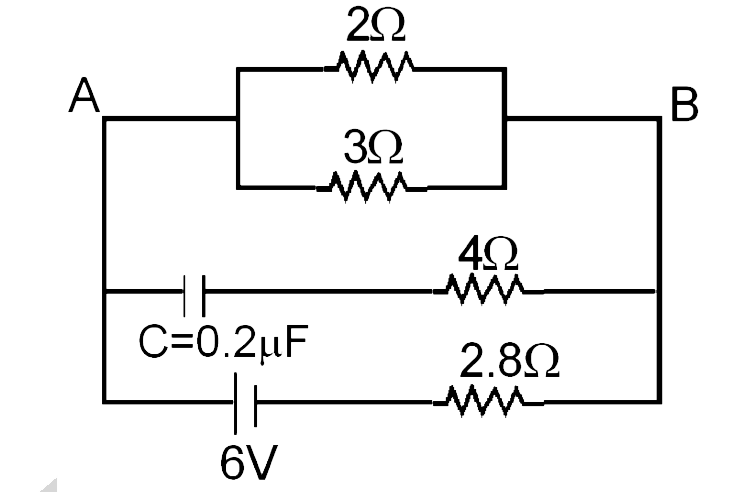
View SolutionIn fig the steady state current in 2ω resistance is
View SolutionIf L and R be the inductance and resistance of the choke coil, then indentify the correct statement
View Solution

