Two this parallel threads carry a uniform charge with linear densities lamnda and −λ . The distance between the threads is equal to l. Find the potential of the electric field and the magnitude of its strength vector at the distance r>>l at the angle θ to the vector 1 (fig).
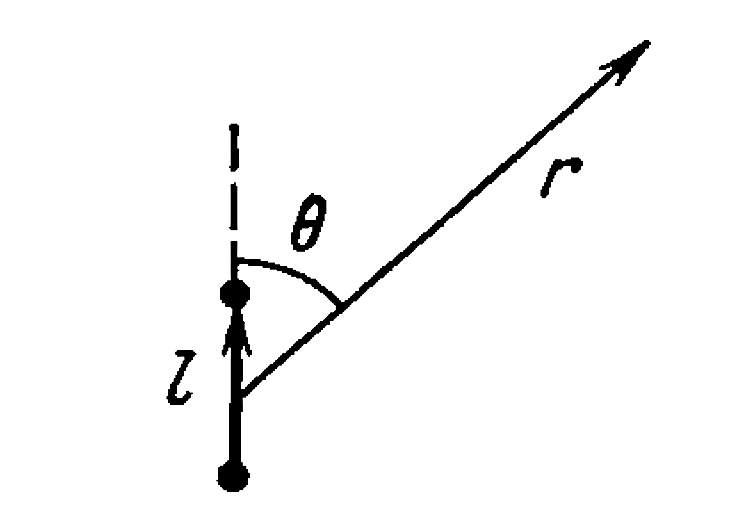
Let p be a point, at distance r>>l and at an angle to θ the vector →l (Fig).
Thus →E at P=λ2πε0→r+→l2∣∣→r+→l2∣∣2−λ2πε0→r−→l2∣∣→r−→l2∣∣2
=λ2πε0⎡⎢⎣→r+→l/2r2+l24+rlcosθ−→r−→l/2r2+l24−rlcosθ⎤⎥⎦
=λ2πε0(→lr2−2l→rr3cosθ)
Hence E=∣∣→E∣∣=λl2πε0r2,r>>1
Also, φ=λ2πε0 In ∣∣→r+→l/2∣∣−λ2πε0 In ∣∣→r−→l/2∣∣
=λ4πε0 In r2+rlcosθ+l2/4r2−rlcosθ+l2/4=λlcosθ2πε0r,r>>l

Topper's Solved these Questions
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Conductors And Dielectrics In An Electric Field
Explore 47 Videos
- ELECTRODYNAMICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRODYNAMICSExercise:Electric Capacitance - Energy Of An Electric Field
Explore 46 Videos
- ELECTRICITY AND MAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTRICITY AND MAGNETISMExercise:All Questions
Explore 6 Videos
- ELECTROMAGNETISMBook:IE IRODOV, LA SENA & SS KROTOVChapter:ELECTROMAGNETISMExercise:All Questions
Explore 24 Videos
Similar Questions
An electric capacitor consists of this round parallel plates. each of radius R, separated by a distance l(l<<R) and uniformly charged with surface densities σ and −σ . Find the potential of the electirc field and the magnitude of tis strength vector at the axes of the capacitor as functions of a distanace x from the plates if x>>l. Investigate and obtained expressions at x>>R.
View SolutionEach of the two long parallel threads carries a uniform charge λ per unit length. The threads are separated by a distance l. Find the maximum magnitude of the electric firld strength in the symmetry plane of theis system located between the threads.
View Solution
Knowledge Check
Two parallel infinite line charges with linear charge densities +λC/m and −λ C/m are placed at a distance of 2R in free space. What is the electric field mid-way between the two line charges?
Aλ2πε0RN/CBzeroC2λπε0RN/CDλπε0RN/CTwo infinitely long thin styraight wires having uniform linear charge densities λ and 2λ are arranged parallel to each other at a distance r apart.The intensity of the electric field at a point midway between them is
A2λπε0Bλπε0rCλ2πε0rD3λ2πε0rAn infinitely long wire with linear charge density +λ is bent and the two parts are inclined at angle 30∘ as shown in fig, the electric field at point P is :
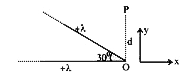 Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]
Aλ4π∈0d[(1+√3)ˆi+ˆj]Bλ4π∈0d[(1−√3)ˆi+2ˆj]Cλ4π∈0d[(1+√3)ˆi−2ˆj]Dλ4π∈0d[(1+√3)ˆi+2ˆj]
A thin infinitely long thread carrying a charge λ per unit length is oriented parallel to the infinite conducting plane. The distance between the thread and the plane is equal to l. Find :
(a) the moducles of the vector of the force acting on a unit length of the thread ,
(b) the disribution of surface chagre density σ(x) over the plane, where x is the distance form the plane perpendicular to the conducting surface and passing through the thread.
View SolutionTwo point charges q and −q are separated by the distance 2l. Find the flux of the electric field strength vector across a circle of radius R.

View SolutionA very long straight thread is oriented at right angles to an infinite conducting plane, its end is separated from the plane by a distance l. The thread carries a uniform charge of linear density λ. Suppose the point O is the trace of the thread on the plane . FInd the surface density of the induced charge on the plane
(a) at point O.
(b) as a function of a distance r from the point O.
View SolutionA thread carrying a unifrom charge λ per unit length has the configuration shown in fig, Assuming a curvature radius R to be considerably less than the length of the thread, find the magnitude fo the electric field strength at the point O.
 ,
, 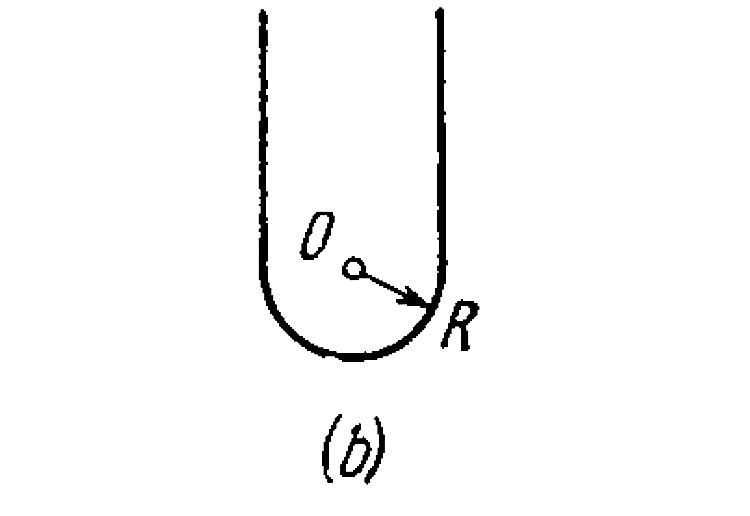
View SolutionThe magnetic field due to current in a straight wire segment of length L at a point on its perpendicular bisector at a distance r(r>>L)
View Solution

