A thread carrying a unifrom charge λ per unit length has the configuration shown in fig, Assuming a curvature radius R to be considerably less than the length of the thread, find the magnitude fo the electric field strength at the point O.
 ,
, 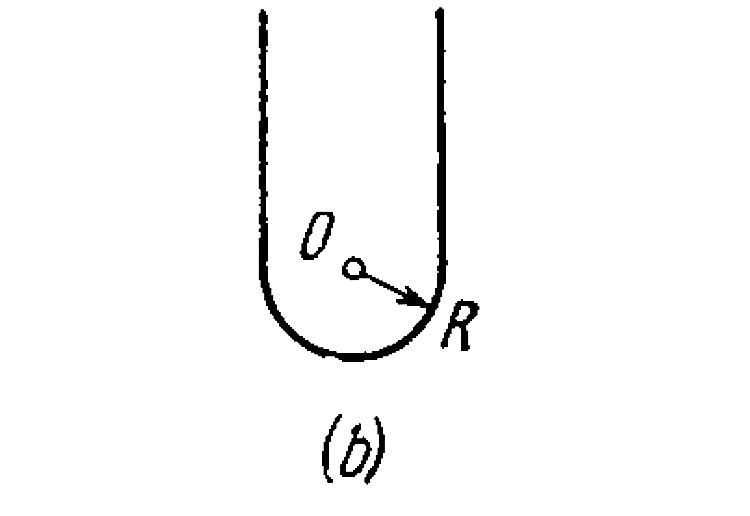
(a) Using the solution of 3.14, the net electric field strength at the point O due to straight parts of the thread equals is zero. For the curved part (arc) let us derive a general expression i.e., Let us calculate the field strength at the centre of arc fo radius R and linear charge density λand which sutends angle θ0 at the centre.
From the symmetry the sought field strength will be directed along the bisector of the angle θ0 and is given by
E=∫+θ0/2−θ0/2(λRdθ4πε0R2)cosθ=λ2πε0Rsinθ02
In our problem θ0=π/2, thus the field strength due to the turned part at the point E0=√2λ4πε0R which is also the sought result.

(b) Using teh solution fo 3.14 (a) net field strength at O due to straight parts equals √2(√2λ4πε0R)=λ2πε0R and is directed vertically down, Now using the solving of 3.15
(a), field strength due to the given curved part (semi-circle) at the point O becomes λ2πε0R and is directed vertically upward. Hence the sought net field strength becomes zero.
Topper's Solved these Questions
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field
47 Videos
- ELECTRODYNAMICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field
46 Videos
- ELECTRICITY AND MAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions
6 Videos
- ELECTROMAGNETISMBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions
24 Videos
Similar Questions
A thin half ring of radius R=20cm is uniformly charged with a total charge q=0.70nC.Find the magnitude of the electric field strength at the curvaite centre of this half-ring.
View SolutionA long wire with a uniform charge density λ is bent in two configurations shown in fig. Determine the electric field intensity at point O.
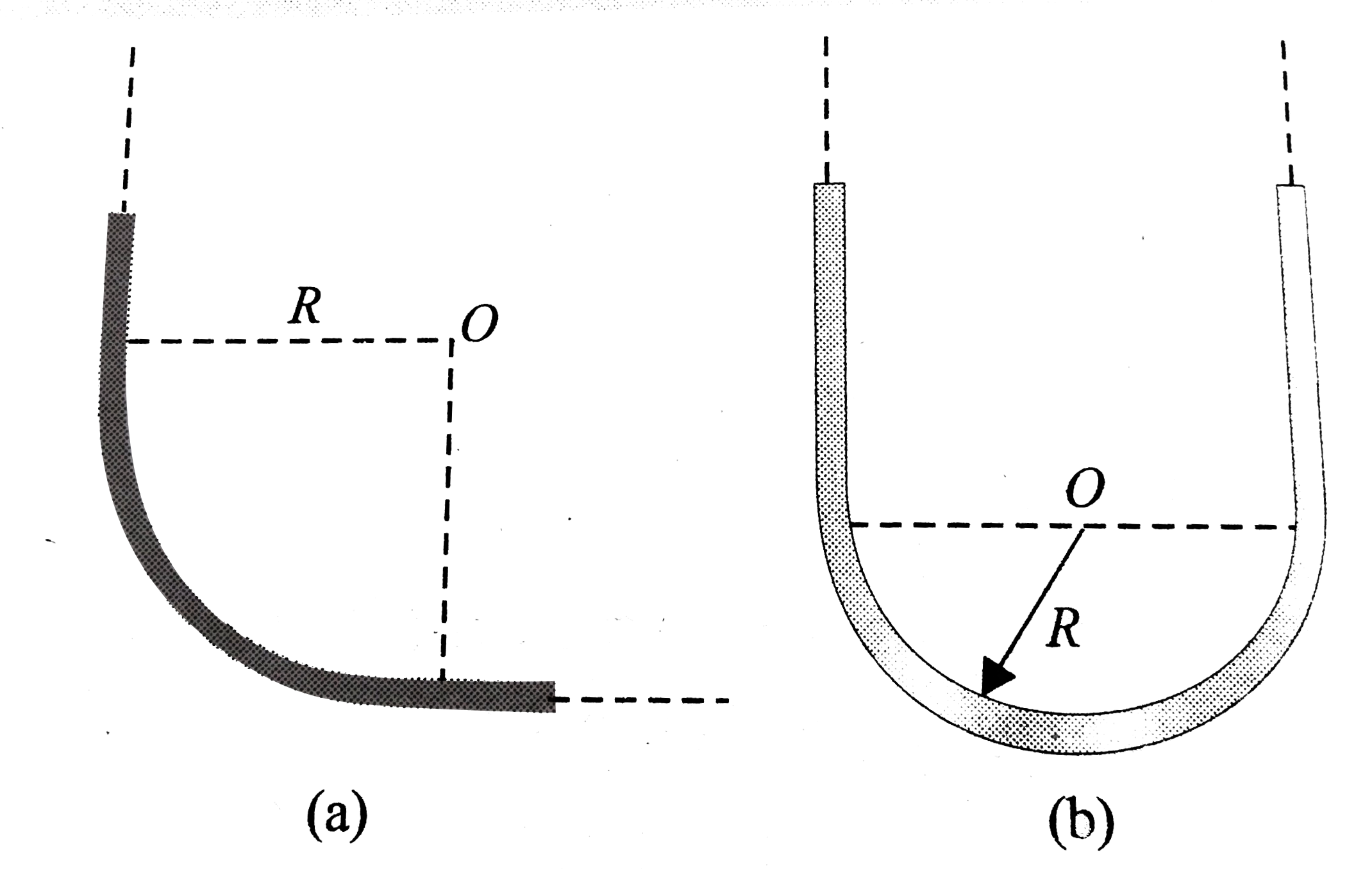
View Solution
Knowledge Check
A spherical shell of radius R has a charge +q units. The electric field due to the shell at a point
Ainside is zero and varies as r−1 outside itBinside is constant and varies as r−2Cinside is zero and varies as r−2 outside itDinside is constant and varies as r−1 outside itA half ring of radius R has a charge of λ per unit length. The electric force on 1C charged placed at the center is
AzeroBkλRC2kλRD(kπλ)RSix point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
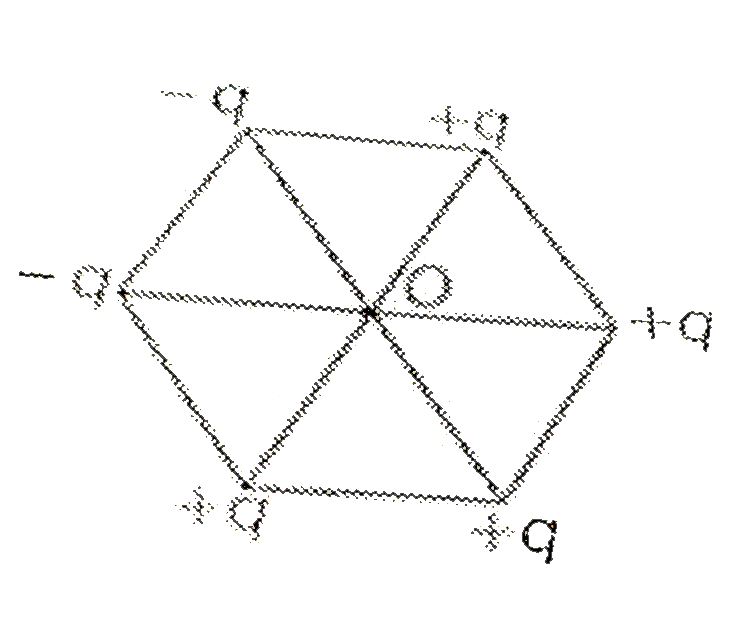
Find the magnitude of electric field at the centre of regular hexagon.Aq4πε0a2BzeroCq2πε0a2Dnone of these
A thin infinitely long thread carrying a charge λ per unit length is oriented parallel to the infinite conducting plane. The distance between the thread and the plane is equal to l. Find :
(a) the moducles of the vector of the force acting on a unit length of the thread ,
(b) the disribution of surface chagre density σ(x) over the plane, where x is the distance form the plane perpendicular to the conducting surface and passing through the thread.
View SolutionA spherical cavity of radius r is made in a conducting sphere of radius 2 r.A charge q is kept at the centre of cavity as shown in the figure.Find the magnitude of the total electric field at (4r 0) .
View SolutionEach of the two long parallel threads carries a uniform charge λ per unit length. The threads are separated by a distance l. Find the maximum magnitude of the electric firld strength in the symmetry plane of theis system located between the threads.
View SolutionA rod of length L has a total charge Q distributed uniformly along its length. It is bent in the shape of a semicircle. Find the magnitude of the electric field at the centre of curvature of the semicircle.
View SolutionA very long straight uniformly charged thread carries a charge λ per unit length. Find the magnitude and direaction of the electric field strength at point which is at a distance y from the thread and lies on the perpendicular passing through one of the thread's ends.
View Solution
