Making use of the Carnot theorem, show that in the same of physically uniform substance whose state is defined by the parameters T and V
(∂U/∂V)T=T(∂p/∂T)v−p
where U(T,V) is the internal energy of the substance.
Consider the infinitesmal Carnot cycle in the variables p,V.
Video Solution
Text Solution
We consider an infinitesimal carnot cycle with isothermal process at temperatures T+dT and T.
Let δA be the work done in the cycle and δQ, be the heat received at the higher temperature. Then by Carnot's theorem
δAδQ1=dTT
On the other hand δA=dpdV=(∂p∂T)vdTdV
while δQ1=dU12+pdV=[(∂U∂V)T+p]dV
Hence (∂U∂V)T+p=T(∂p∂T)v.
 .
.
|
Topper's Solved these Questions
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Liquids Capillary Effects
Explore 25 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Phase Transformations
Explore 35 Videos
- THERMODYNAMICS AND MOLECULAR PHYSICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:THERMODYNAMICS AND MOLECULAR PHYSICSExercise:Kinetic Theory Of Gases
Explore 51 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBook:IE IRODOV, LA SENA & SS KROTOVChapter:PHYSICAL FUNDAMENTALS OF MECHANICSExercise:Relativistic Mechanics
Explore 49 Videos
Similar Questions
Knowledge Check
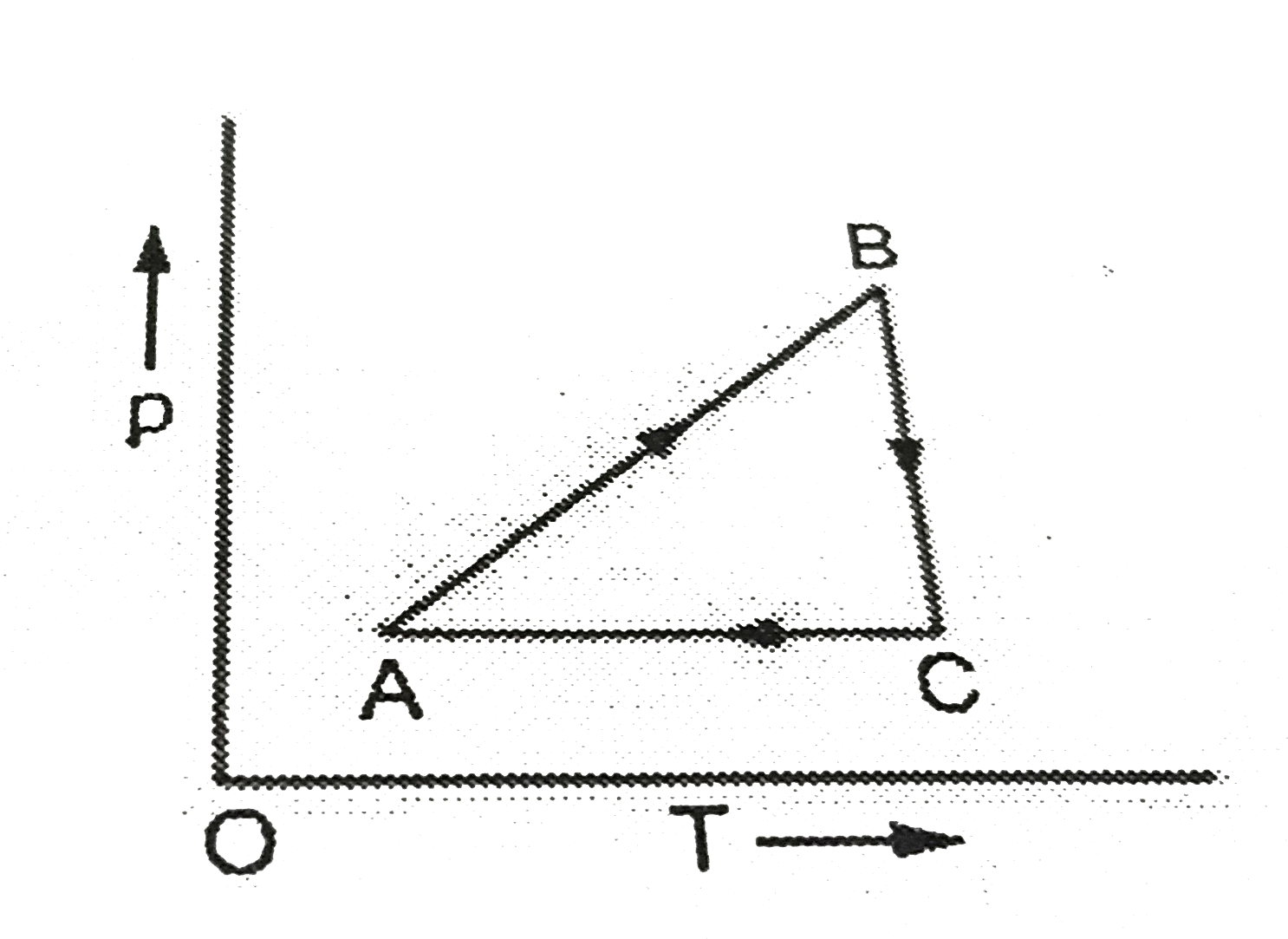
A cyclic process is shown in the P−T diagram.
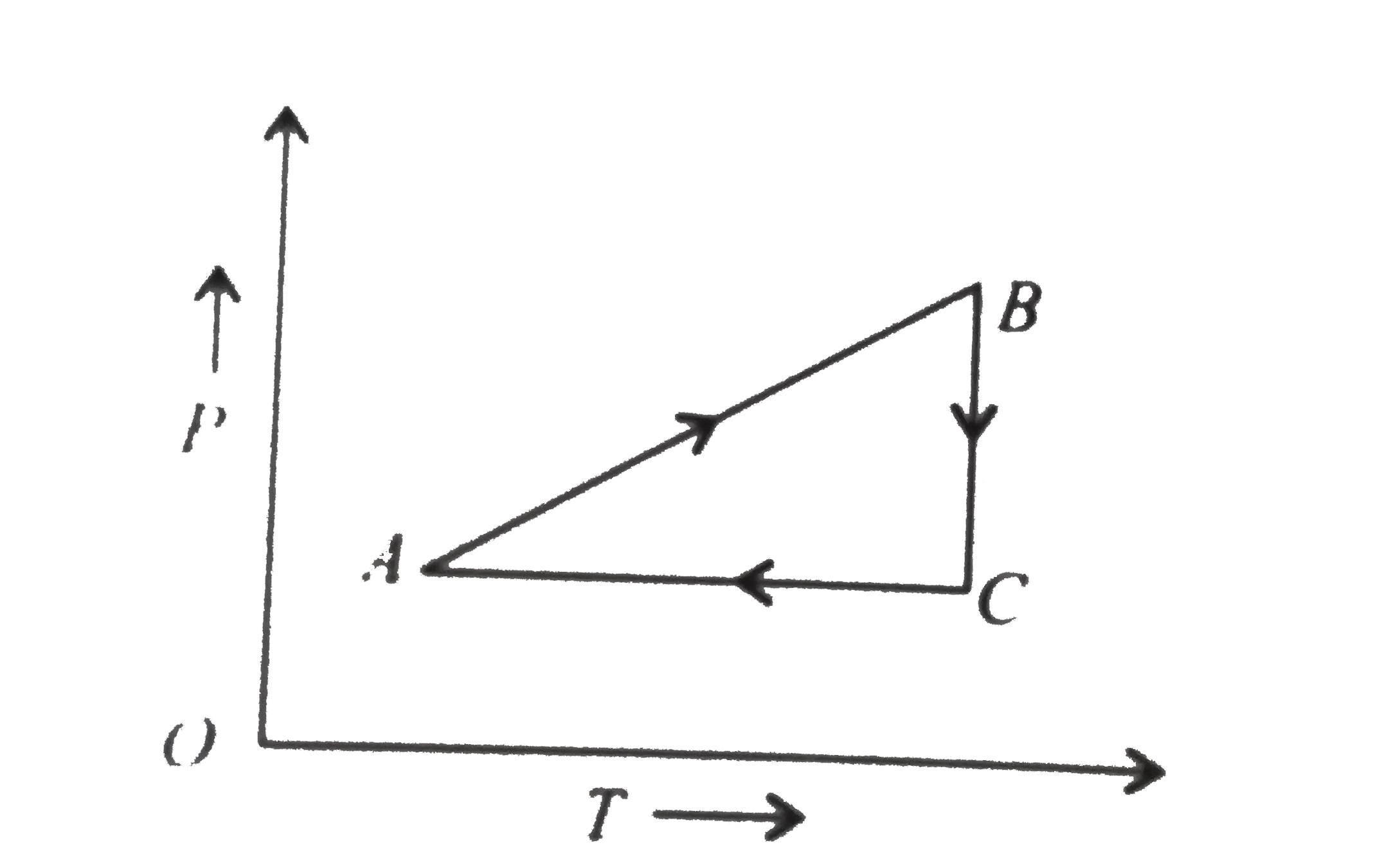
Which of the curve shows the same process on a V−T diagram?A B
B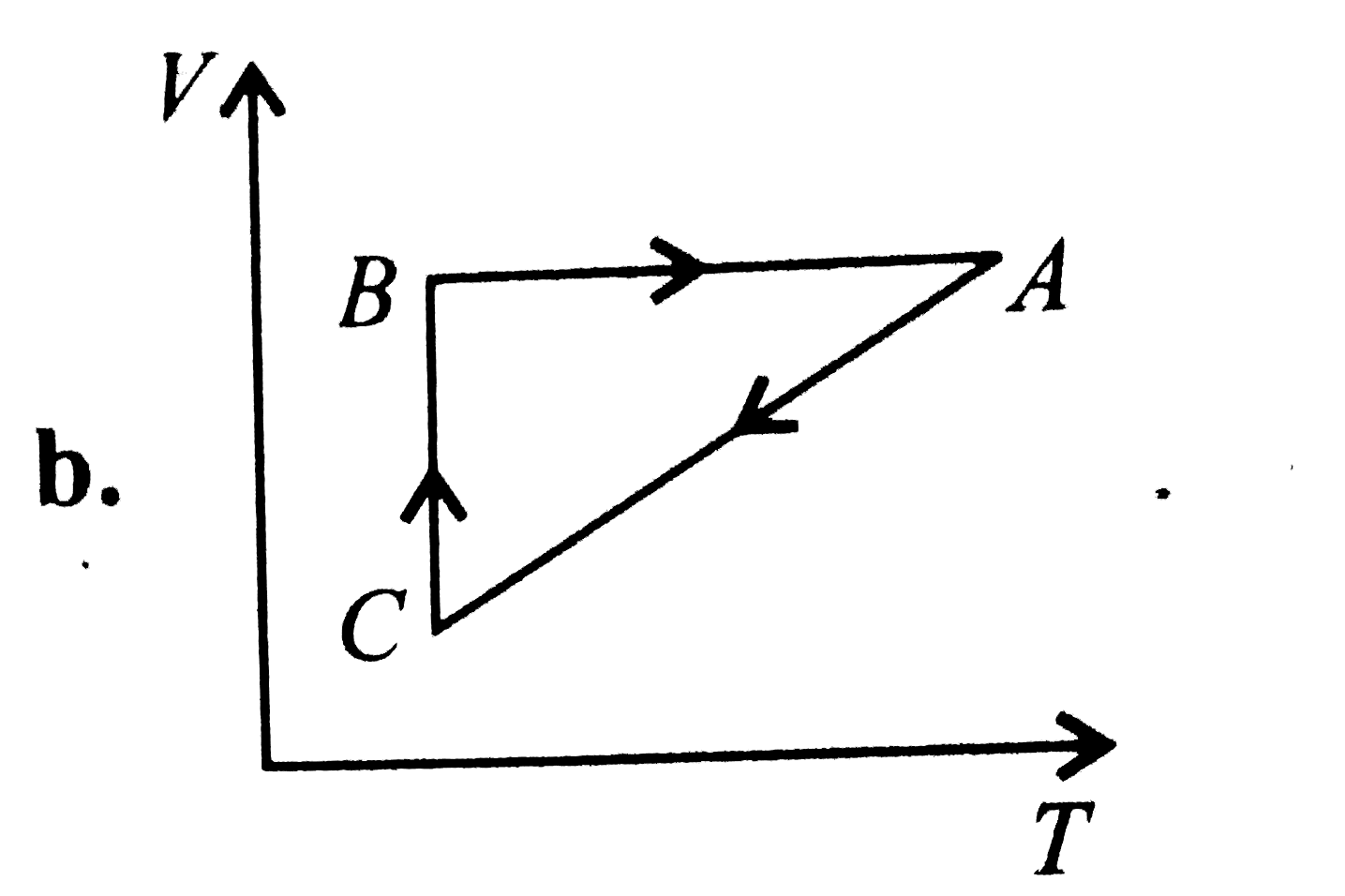 C
C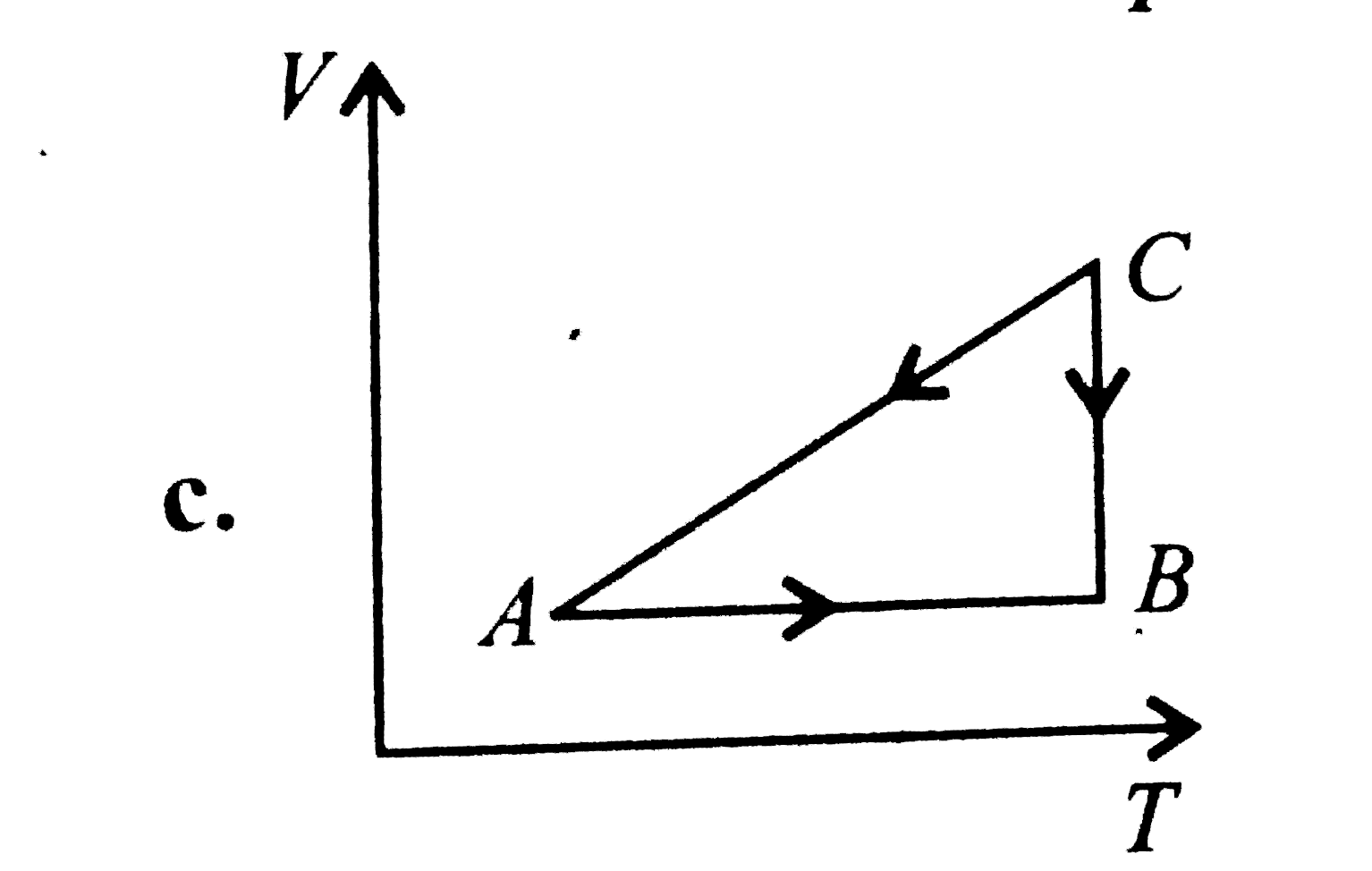 D
D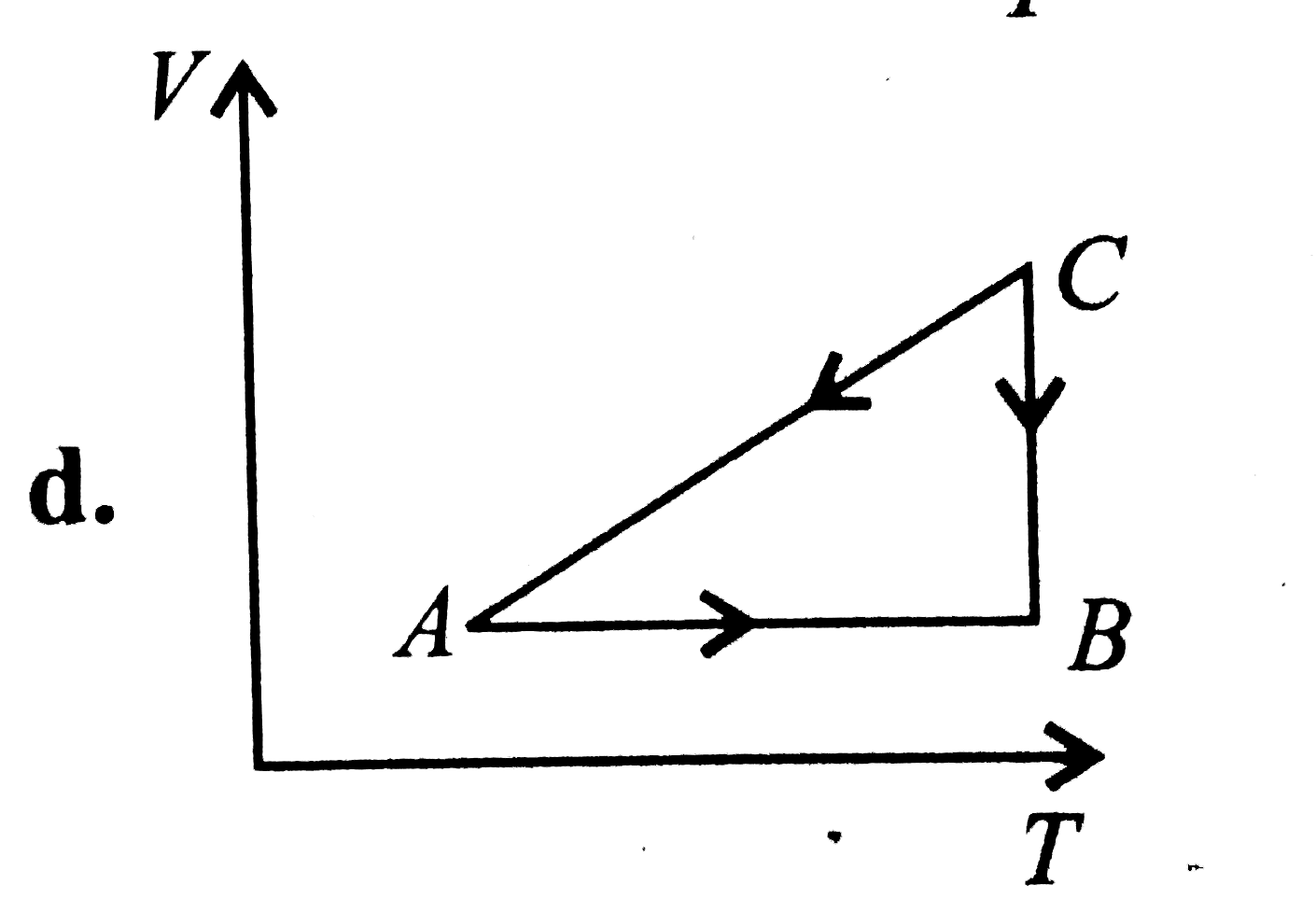
For one mole of an ideal gas (δPδT)V(δVδT)P(δVδP)T=
A−1BR2P2CR2P2D+1P-V curve is shown for a Carnot engine. Answer the question from the graph.
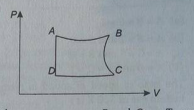
If the temperature at B and C are T1 and T2 respectively, then it can be concluded :AT1=T2BT1>T2CT1<T2Dnothing can be said about T1/T2
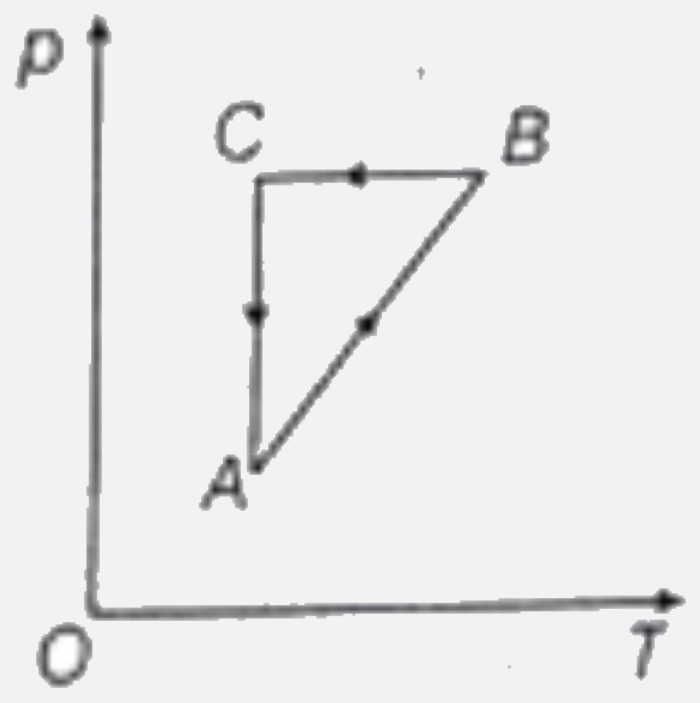
A cyclic process is shown in the p-T diagram. Which of the curves show the same process on a V-T diagram?
View SolutionA cyclic process is shown in the p – T diagram . Which of the following curves shows the same process on the p – V diagram ?
View SolutionFind the isothermal compressibility x of a Van der Walls gas as a function of volume V at temperature T
By definition, x=−1V∂V∂p.
View SolutionA cyclic process is shown in theP–T diagram. Which of the curves show the same process on a V–T diagram?
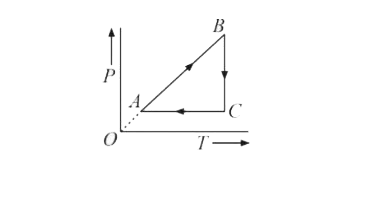
View SolutionP-V curve is shown for a Carnot engine. Answer the question from the graph.

If the temperature at B and C are T1 and T2 respectively, then it can be concluded :
View Solution

