A horizontal tube with closed ends is rotated with a constant angular velocity ω about a vertical axis passing through one of its ends. The tube contains carbon dioxide at a temperature T=300K. The length of the tube is l=100cm. Find the value ω at which the ratio of molecular concentrations at the opposite ends of the tube is equal to η=2.0.
The potential energy associated with each molecule is : −12mω2r2
and there is a concentration variation
n(r)=n0exp(mω2r22kT)=n0exp(mω2r22RT)
Thus η=exp(Mω2l22RTor ω=√2RTMl21nη
Using M=12+32=44gm,l=100cm,R=8.31×107erg.∘K,T=300,
we get ω=280 radians per second.
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - The Second Law Of Thermodynamics - Entropy47videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - Liquids Capillary Effects25videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - THERMODYNAMICS AND MOLECULAR PHYSICSEXERCISE - The First Law Of Thermodynamics - Heat Capacity36videos
THERMODYNAMICS AND MOLECULAR PHYSICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
Similar Questions
A horizontal cylinder closed from one end is rotated with a constant angular velocity ω about a vertical axis passing through the open end of the cylinder. The outside air pressure is equal to p0, the temperature to T, and the molar mass of air to M. find the air pressure as a function of the distance r from the rotate axis. The molar mass is assumed to be independent of r.
View SolutionA horizontal oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO' passing thorugh the end A figure. The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. find the velocity of the fluid relative to the tube as a function of the column height h.
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl] - Question 2 - Select One
A thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
Amω2l26AYBmω2l23AYCmω2l2AYDmω2l22AY - Question 3 - Select One
For an L shaped conducting rod placed in an uniform magnetic field →B rotating with constant angular velocity ω about an axis passing through one of its ends A and normal to the plane of the conductor induced emf
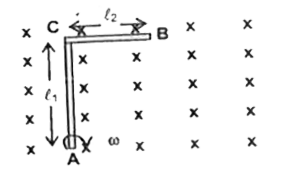Aacross AC equals ωBl21Bacross AC equals 12ωBl21Cacross BC equals zeroDNone of the above is correct
_S01_079_Q01.png)
A horizontal oriented tube AB of length 5m rotates with a constant angular velocity 0.5 rad/s about a stationary vertical axis OO' passing through the end A. the tube is filled with ideal fluid. The end of the tube is open, the closed end B has a very small orifice. The velocity with which the liquid comes out from the hole (in m/s) isView SolutionA horizontally oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO′ passing through the end A (figure). The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View SolutionA horizontally orientd tube of length l rotates with a constant angular velocity ω about a stationary vertical axis. XX passing through end A. The tube is filled with ideal fluid.
The end A of tube is having pressure P0. The closed end B has a small hole and at time t = 0, the fluid column has length of l. Find velocity of fluid relative to tube at the instant t = 0
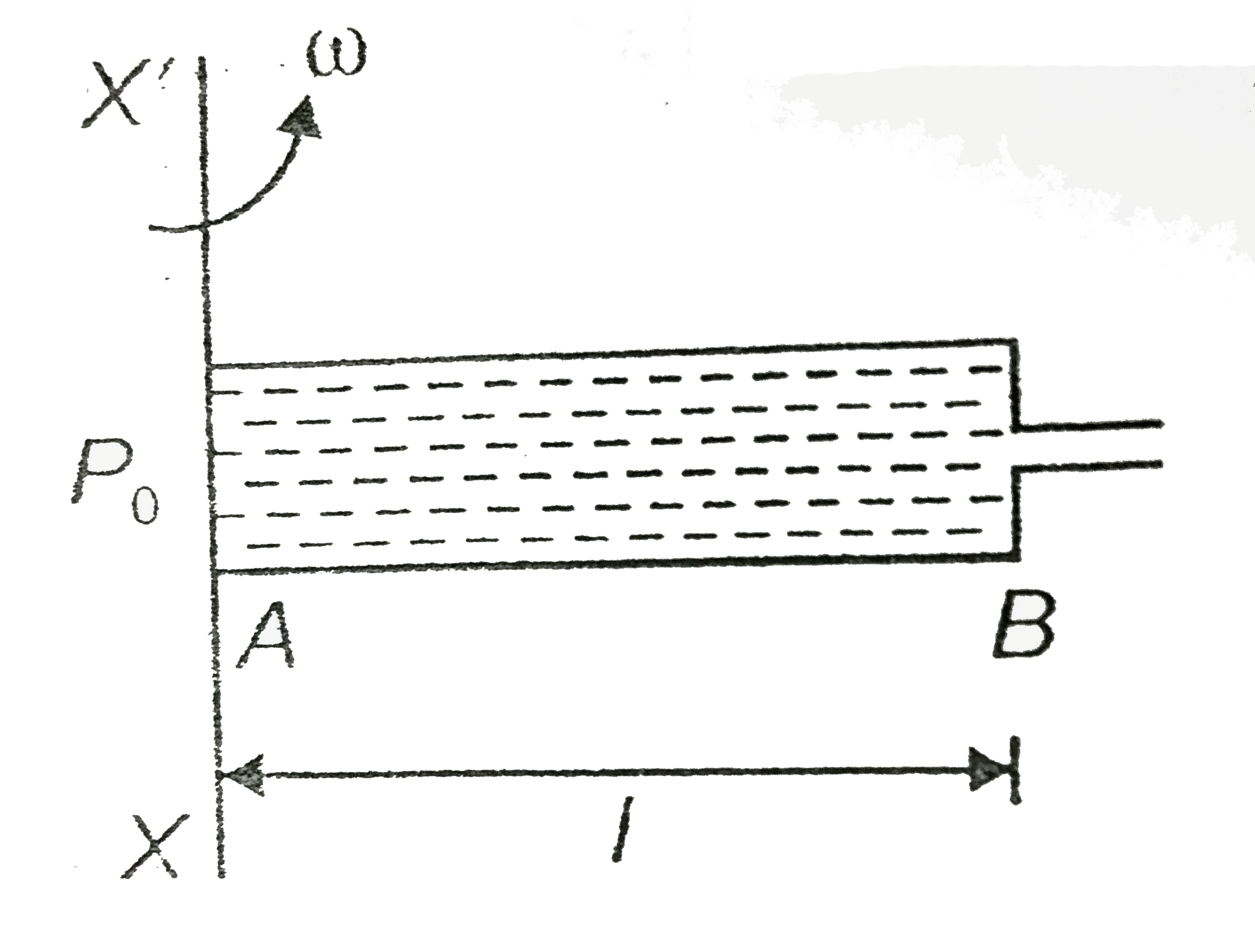
View SolutionA horizontally oriented bent thin tube ABC of length 1.4m rotates with a constant angular velocity ω about a stationary vertical axis OO' passing through the end A as shown in figure. The portion BC of tube is parallel to OO' and its length is equal 0.4m. At t=0, AB part of tube is filled with an ideal fluid. The end A of tube is open, the closed end C has a very small orifice. Find the maximum height reached by fluid relative to end C. (take g=10/s2 and ω=10rad/s)
View Solution